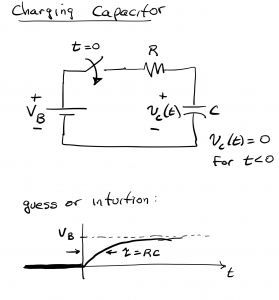
7.3 Charging capacitor
We now examine the case of a capacitor being charged by a battery in the circuit shown. We assume the capacitor is initially un-charged (that is, vc(t)=0 for t<0). The switch is closed at t=0, and current begins to flow from the battery into the series-connected resistor and capacitor. The voltage across the capacitor increases as the current flows, and the capacitor asymptotically approaches voltage VB.
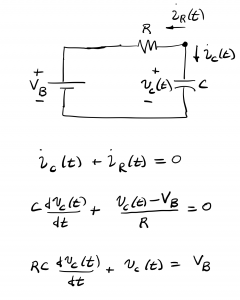
Analysis begins by applying KCL to the node shown, and proceeding as in the previous chapter to develop the first order linear differential equation.
This differential equation is similar to the one developed in the previous chapter with the addition of the forcing function, VB. An educated guess at the form of solution with three constants to be determined, follows:

The solution at this point is nearly complete, but the remaining constant K2 needs to be determined by applying the boundary condition:
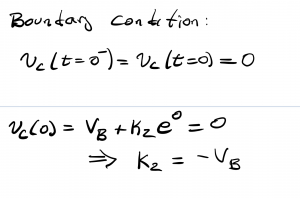
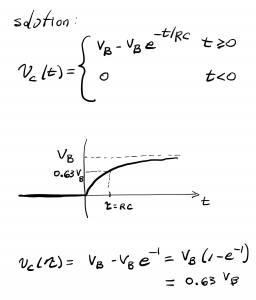
We finally arrive at the solution for vc(t). The capacitor voltage increases from an initial value of 0, exponentially increasing and asymptotically approaching VB. An approximate value for the duration of the transient is T=RC seconds.