2.6 Circuit Laws: KCL and KVL

We now introduce two laws for analyzing circuits that we will be using for the duration of this text.

Kirchoff’s Current Law. We previously defined a node in a circuit as a point where two or more circuit elements are connected together.  Kirchoff’s current law (typically written “KCL”) specifies that the the sum of all currents entering a node must equal the sum of all currents exiting a node.

 

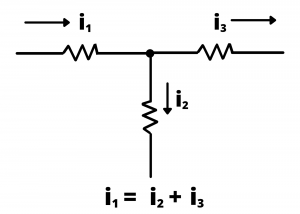
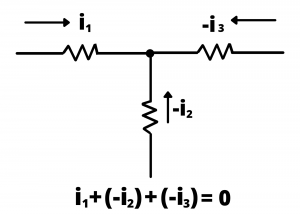
Figure 2.47 Kirchoff’s Current Law (KCL) states that the sum of currents entering any circuit node must equal the sum of currents exiting the node.

Put another way, the net current entering (or exiting) any circuit node must equal zero.  This law amounts to a statement of conservation of charge: if the net current entering any node were non-zero, there would be a net buildup of charge at a point in a circuit over time. The analogy with a hydraulic piping system is helpful: if a series of pipes come together at a junction, the total fluid flow, in gallons per minute or cubic meters per second, entering the junction must equal the total fluid flow exiting the junction, otherwise there would be a buildup of fluid over time. Figure 2.47  is redrawn below to show all currents entering the circuit node with no currents exiting the node. KCL then specifies that the total current entering the node is i_{1}+(-i_{2})+(-i_{3})=0. Note that negative signs are used for i_{2} and i_{3} to represent the currents of Figure 2.47 as entering the node when we draw Figure 2.48.

Figure 2.48 KCL states that the net current entering (or exiting) any node in a circuit must be zero

Implication for circuit elements connected in series.  We previously defined series circuit elements as elements connected end-to-end, with no additional path for current to flow. Implicit in this definition is that the currents in series-connected elements are identical.

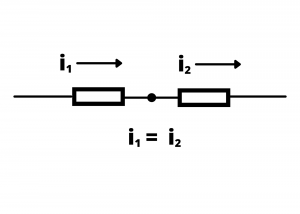
Figure 2.49 KCL implies that circuit elements connected in series must have identical currents

This can be shown via straightforward application of Kirchoff’s Current Law, where, for the single node in Figure 2.49,  i_{1}=i_{2}  by KCL.  This can be readily extended to more than two circuit elements combined in series, allowing us to state: all circuit elements connected in series have the same value of current. 

Examples

Determine the value of current I_{3} in the circuit shown:

Figure 2.50

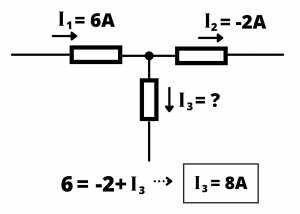
Solution: letting the sum of currents entering the node equal the sum of currents exiting the node, we have:    6= -2 + I_{3} or I_{3} = 8 A.

 

Determine the value of the current I_{3} in the circuit shown:

Figure 2.51

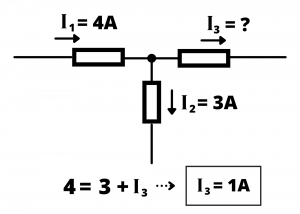
Solution: proceeding as in the previous example:  4= 3 + I_{3} or I_{3}=1 A.

Note that in these two examples and in Figures 2.50 and 2.51, we use the variables I_{1}, I_{2} and I_{3} whereas we used variables i_{1}, i_{2}, and i_{3} in figures 2.47 and 2.48. This is keeping with our convention of using upper case variables to represent DC values, as in these two examples, while using lower case variables to represent the more general case of AC and mixed AC+DC values.

 

 

Kirchoff’s Voltage Law. We previously defined a loop in a circuit as a closed path starting at a node, proceeding through circuit elements, ultimately returning to the starting node.  Kirchoff’s voltage law (KVL) stipulates that the sum of voltages encountered traversing any closed circuit loop must equal zero. This law amounts to a statement of conservation of energy. The circuit shown in figure 2.52 has four series-connected elements and four nodes, which we label A-D.

Figure 2.52 Circuit with four elements and four nodes. Loops are drawn around ABCDA (inside loop) and BADCB (outer loop)

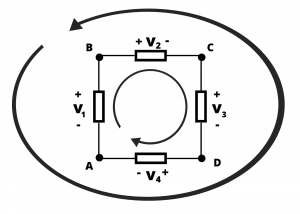
Two loops are shown: a clockwise inner-loop and a counter-clockwise outer loop. Applying KVL clockwise around the inner-loop, starting at node A and proceeding through nodes B, C, and D, and back to A (we write this as ABCDA), we have:

(1)   \begin{equation*} -v_{1}+v_{2}+v_{3}+v_{4}=0 \end{equation*}

Note that we use the first voltage polarity encountered to determine whether to add or subtract the voltage of an element between nodes, thus, between A and B, we have -v_{1}, while between B and C we have +v_{2}, since we first encounter the - terminal of v_{1} and the + terminal of v_{2} when proceeding clockwise around loop ABCDA. Similarly, we could apply KVL counterclockwise around the outer-loop BADCB, with the result

(2)   \begin{equation*} v_{1}-v_{4}-v_{3}+v_{2}=0 \end{equation*}

Inspection of equations (1) and (2) reveals that they are equivalent.  It does not matter where in a closed loop one starts summing a KVL equation or in which direction (clockwise or counter-clockwise) one proceeds. KVL  sums around ADCBA, DCBAD, CBADC, CDABC, etc… all result in the same KVL equation.

Examples

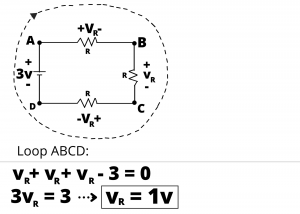
Example:  Write the KVL equation around the loop ABCD in the circuit shown.

Figure 2.53

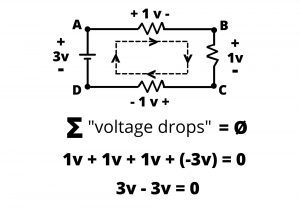
Example: Use KVL to solve for the voltage V_{R} in the circuit shown, where V_{R} is the voltage drop across the three resistors, R.

Figure 2.54

 

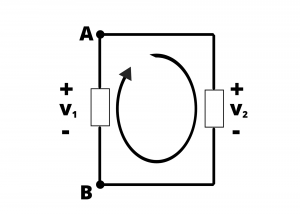
Implication for circuit elements connected in parallel:  We previously defined  parallel circuit elements as elements having their two ends connected to each other as shown, for example, in figure 2.55. Implicit in this definition is that the voltages across parallel-connected elements are identical. This can be shown via straightforward application of Kirchoff’s Voltage  Law, where, for the single loop circuit shown, KVL around loop ABA gives us v_{2}-v_{1}=0 which results in v_{1}=v_{2}.

Figure 2.55 KVL around the loop ABA shows that v_{1}=v_{2}

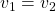
This can be readily extended to more than two circuit elements combined in parallel, allowing us to state: all circuit elements connected in parallel have the same voltage across their terminals. 

Examples

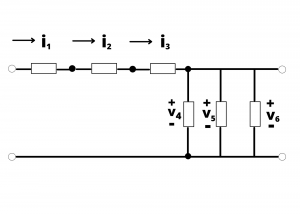
Example: In the circuit shown in Figure 2.56, which elements are connected in series and which are in parallel? What are the implications for the voltages and currents in the circuit?

Solution: Elements 1, 2, and 3 are connected in series, therefore, i_{1}=i_{2}=i_{3}. Elements 4, 5, and 6 are connected in parallel, therefore v_{4}=v_{5}=v_{6}.

Figure 2.56

 

 

 

 

 

 

 

 

License

Icon for the Creative Commons Attribution 4.0 International License

Applied Electrical Engineering Fundamentals by David J. McLaughlin is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book