2.8 Power and energy in resistive circuits
We now consider the power and energy absorbed by resistors and supplied by sources in more detail. Recall that a voltage drop (a decrease in electric potential) across a circuit element in the direction of positive current flow represents energy absorbed. This is the case when current moves through a resistor. A voltage rise (an increase in electric potential) across a circuit element in the direction of positive current flow represents energy being supplied by the circuit element. This is the case when a battery supplies power to a circuit. In either case, energy is being transferred (such as being converted to heat or being supplied to the circuit) at a rate of
(1) ![]()
which has units of watts or ![]() . To better understand eq (1), we can rewrite the equation in terms of the unit dimensions for power, voltage and current
. To better understand eq (1), we can rewrite the equation in terms of the unit dimensions for power, voltage and current
(2) ![]()
For a resistor, Ohm’s law equations ![]() and
and ![]() can be used in eq (1) to obtain
can be used in eq (1) to obtain
(3) ![]()
and
(4) ![]()
respectively. Equations (1), (3) and (4) are all useful for for determining the power absorbed by a resistor.
Energy supplied or absorbed. Since power is the rate of transfer of energy (![]() ) The total energy transferred over a time interval
) The total energy transferred over a time interval ![]() seconds long from
seconds long from ![]() to
to ![]() is given by
is given by
(5) ![]()
Note that we have explicitly noted the time dependence for voltage ![]() , current
, current ![]() and power
and power ![]() in the expressions discussed above. This makes it easier to remember that AC waveforms vary as functions of time. Below, we consider DC and AC circuits and power calculations, and we will find, not surprisingly, that
in the expressions discussed above. This makes it easier to remember that AC waveforms vary as functions of time. Below, we consider DC and AC circuits and power calculations, and we will find, not surprisingly, that ![]() is constant for DC circuits while
is constant for DC circuits while ![]() varies with time for AC circuits. Looking ahead, we will develop expressions for computing average power when
varies with time for AC circuits. Looking ahead, we will develop expressions for computing average power when ![]() fluctuates with time, and we will find that, for circuits comprised of resistors and sources, the average power is conveniently related to the RMS values of voltage and current.
fluctuates with time, and we will find that, for circuits comprised of resistors and sources, the average power is conveniently related to the RMS values of voltage and current.
DC circuit example. Consider the circuit shown in figure 2.70 where ![]() is a DC voltage given by
is a DC voltage given by
(6) ![]()
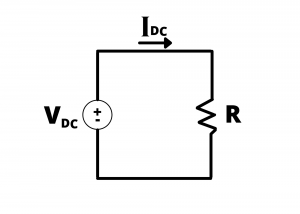
The power absorbed by the resistor is, using (3)
(7) ![]()
and the amount of energy absorbed by the resistor over the time interval from ![]() to
to ![]() is
is
(8) ![]()
Examples
Example: If ![]() in Figure 2.70 were
in Figure 2.70 were ![]() and
and ![]() how much energy would be absorbed by the resistor in 10 seconds? 100 seconds? for all time?
how much energy would be absorbed by the resistor in 10 seconds? 100 seconds? for all time?
Solution: By eq (8), ![]() for
for ![]() . For
. For ![]()
![]() . For all time,
. For all time, ![]() would be infinite. This, of course, is not practical, but neither is it practical to have a voltage source that lasts for all of time.
would be infinite. This, of course, is not practical, but neither is it practical to have a voltage source that lasts for all of time.
Example: If ![]() in Figure 2.70 were
in Figure 2.70 were ![]() and
and ![]() how long would it take until all the energy in the batteries was depleted if the
how long would it take until all the energy in the batteries was depleted if the ![]() power supply was comprised of four fresh AA batteries wired in series, each containing 10kJ of energy when new.
power supply was comprised of four fresh AA batteries wired in series, each containing 10kJ of energy when new.
Solution: The total energy from the batteries is ![]() . From eq (7) the circuit is consuming energy at a rate
. From eq (7) the circuit is consuming energy at a rate ![]() . The battery’s energy will be consumed in
. The battery’s energy will be consumed in ![]() or
or ![]() hours (hr).
hours (hr).
AC circuit example. We now consider the power and energy associated with resistive circuits driven by AC sources. Consider the circuit shown in figure 2.70 where ![]() is an AC voltage source given by
is an AC voltage source given by
(9) ![]()
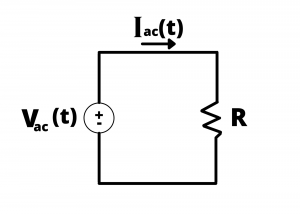
The current is given by
(10) ![]()
The instantaneous power absorbed by the resistor is, using (3)
(11) ![]()
The instantaneous waveforms for ![]() ,
, ![]() , and
, and ![]() are plotted in figure 2.71 for time from
are plotted in figure 2.71 for time from ![]() to
to ![]() seconds. Note how the voltage oscillates between peak-to-peak values
seconds. Note how the voltage oscillates between peak-to-peak values ![]() to
to ![]() over time, while current simultaneously oscillates between peak-to-peak values
over time, while current simultaneously oscillates between peak-to-peak values ![]() to
to ![]() amps. The RMS value for the voltage,
amps. The RMS value for the voltage,
(12) 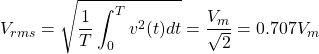
is shown as a dashed line in the ![]() plot. Likewise, the RMS value for the current, which is
plot. Likewise, the RMS value for the current, which is ![]() or
or ![]() times the peak value, is shown as a dashed line on the
times the peak value, is shown as a dashed line on the ![]() plot.
plot.
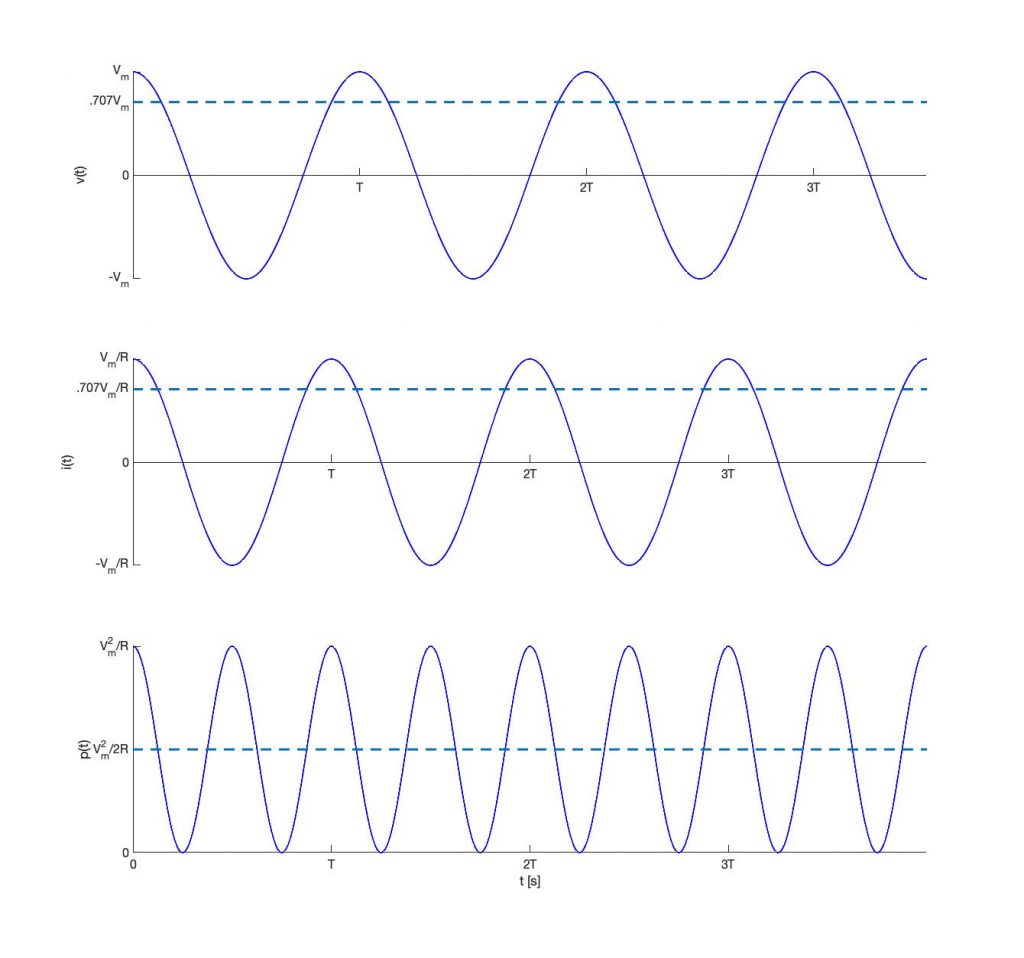
Owing to the sinusoidal character of the voltage and current waveforms, the instantaneous power also has a sinusoidal character. The instantaneous power ![]() has the shape of a raised cosine oscillating at twice the frequency of
has the shape of a raised cosine oscillating at twice the frequency of ![]() ; this is evident when we apply the trigonometric identity:
; this is evident when we apply the trigonometric identity:
(13) ![]()
to eq (11) to give
(14) ![]()
The average power, computed as
(15) ![]()
is plotted as a dashed line on the ![]() plot of figure 2.71.
plot of figure 2.71.
Note that the product of the RMS voltage and RMS current is equal to the average power:
(16) ![]()
which gives
(17) ![]()
Recall that power is the rate at which energy is absorbed. The total amount of energy absorbed by resistor ![]() between
between ![]() and
and ![]() seconds is, from eq(5)
seconds is, from eq(5)
(18) ![]()
If ![]() is a multiple of
is a multiple of ![]() then the
then the ![]() integrand of eq (19) evaluates to zero, and we have
integrand of eq (19) evaluates to zero, and we have
(19) ![]()
Note the use of ![]() and
and ![]() in these equations.
in these equations. ![]() refers to the repetition period of the periodic waveforms under consideration. All of the structure of a periodic waveform is represented in a time interval
refers to the repetition period of the periodic waveforms under consideration. All of the structure of a periodic waveform is represented in a time interval ![]() seconds long, and we can actually carry out integrals over any duration
seconds long, and we can actually carry out integrals over any duration ![]() seconds wide, although we are using the internal from
seconds wide, although we are using the internal from ![]() to
to ![]() seconds here. The variable
seconds here. The variable ![]() represents the duration over which we are calculating energy absorbed, and this need not be related to T. As an example, we might want to determine how much energy is absorbed by a household appliance over a day. Since household electricity in the USA oscillates at 60 Hz, calculations would use
represents the duration over which we are calculating energy absorbed, and this need not be related to T. As an example, we might want to determine how much energy is absorbed by a household appliance over a day. Since household electricity in the USA oscillates at 60 Hz, calculations would use ![]() , while
, while ![]() is the number of seconds in a day.
is the number of seconds in a day.
Average power for periodic waveforms. The results given above relating the average power and the total energy over a finite time interval to the RMS voltage have been derived specifically for the case of a sinusoidal waveform, but these results are valid for any periodic waveform. This is apparent when we write the equation for average power:
(20) ![]()
for a resistor, ![]() and equation (20) can be written as
and equation (20) can be written as
(21) ![]()
when ![]() is removed from the integral, and when we recall the definition previously given for the RMS voltage:
is removed from the integral, and when we recall the definition previously given for the RMS voltage:
(22) 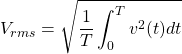
we have the result
(23) ![]()

