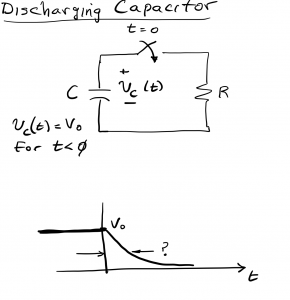
7.2 Discharging Capacitor
We begin by considering a circuit comprising a capacitor and resistor connected through a switch as shown. Assume the capacitor has an initial voltage Vo, and at time t=0, the switch is closed, resulting with a circuit in which R and C are in parallel. Our objective is to determine the voltage across the capacitor as a function of time, vc(t). We will achieve this objective by using circuit analysis tools (eg, KCL, KVL, Ohm’s law, the V-I relationships for the capacitor, etc…) that will lead to a first order differential equation, which we will solve. Before we being the analysis, we provide a sketch showing what vc(t) might look like as a function of time. For t<0, we know that vc(t)=Vo; closing the switch at t=0 allows current to flow in the circuit, as stored energy from the capacitor is released and dissipated as heat in the resistor. The capacitor voltage exponentially decays with time, asymptotically approaching zero.
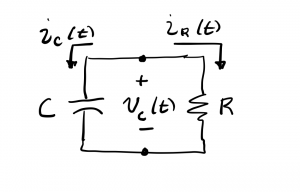
Analysis begins by performing KCL at the top node shown, and taking note of the fact that the vc(t) is the voltage across both R and C, as they are connected in parallel.
Applying the I-V relationships between current and voltage for the capacitor and the resistor, results in the first-order linear differential equation shown. A standard approach for solving differential equations such as this is to make an educated guess at the form of the solution, as shown.
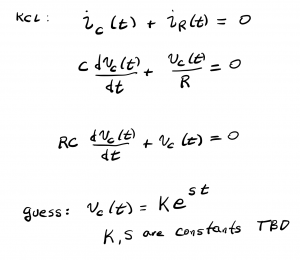
Inserting the guessed solution back into the differential equation allows us to begin solving for the unknown constant, s.
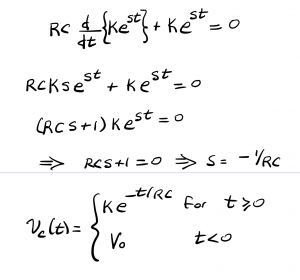
At this point, we have the solution but have a remaining constant, K, to determine. Applying the boundary condition vc(0)=Vo yields this constant.

Finally, we have the solution for vc(t) for all time, given and plotted below. While the exponential decay lasts forever, an approximate value for the duration for this transient signal is T=RC seconds.


