6.4 Negative Feedback Amplifier
Op amp circuits can achieve controlled voltage gain while avoiding saturation by employing negative feedback. The basic idea is to provide a path between the op amp output node, which has voltage Vo, and the inverting terminal input node, which has voltage V–. In the example circuit shown in figure 6.22, this is accomplished via the feedback resistor Rf.
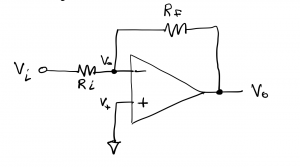
This feedback path serves to subtract part of the output voltage from the differential input voltage as a way to avoid saturation by the very high gain amplifier, A. The impact of feedback is to drive the differential input voltage (V+-V–) toward a very small value (ideally, zero). When multiplied by the very large (ideally, infinite) open-loop gain, ![]() , the output voltage
, the output voltage ![]() remains finite and the op amp avoids saturation. Read the last three sentences again and think about what is written. Repeat.
remains finite and the op amp avoids saturation. Read the last three sentences again and think about what is written. Repeat.
How negative feedback works. We begin by considering the closed-loop feedback amplifier block diagram shown in figure 6.23. This circuit has the same function as the op amp circuit shown above, but it is implemented more simply with three functional blocks (when we say “functional” we mean that we will concern ourselves with what the block does, rather than what the block is or how the functionality is achieved; we don’t care what’s inside the block): a difference block that subtracts one signal from another, and two amplifier blocks, a forward amplifier having gain A and a reverse, or backward amplifier, having gain f. (Forward and backward just refer to the input-output flow direction of the amplifiers: left to right in the forward case and right to left in the backward case.) The amplifier blocks simplify multiply their respective inputs by A and f to produce output signals. Given these definitions, we can readily derive the input-output relationship, ![]() vs.
vs. ![]() for this circuit by inspecting the block diagram:
for this circuit by inspecting the block diagram:
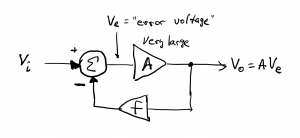
![]() , defined as the “error voltage”, is the difference between the input signal
, defined as the “error voltage”, is the difference between the input signal ![]() and the output signal
and the output signal ![]() , having been amplified by backward gain f. This is called an error voltage in control theory because it often represents the difference between a desired value and an achieved value. As we shall see, this voltage is driven to zero by the feedback circuit.
, having been amplified by backward gain f. This is called an error voltage in control theory because it often represents the difference between a desired value and an achieved value. As we shall see, this voltage is driven to zero by the feedback circuit.
The error voltage is given by
(1) ![]()
![]() is an amplified version of the error voltage,
is an amplified version of the error voltage,
(2) ![]()
Substituting, eq. (1) into eq. (2) we have
(3) ![]()
from which we obtain, via algebraic manipulation:
(4) ![]()
and then
(5) ![]()
We know that op amps have very large (ideally, infinite) values of A, so we want to examine the behavior of this input-output relationship for very large A. To do this, we divide numerator and denominator by A, achieving
(6) ![]()
The closed-loop gain is given by
(7) ![]()
when we let A become very large, ![]() becomes negligible and we have
becomes negligible and we have
(8) ![]()
For the ideal op amp with A=∞, eq. (8) is an equality rather than an approximation since ![]() .
.
Note that the closed-loop gain of the circuit, ![]() , is independent of gain
, is independent of gain ![]() . All that was required was that
. All that was required was that ![]() be very large compared with
be very large compared with ![]() .
. ![]() , which we refer to as the open-loop gain, serves an important role in the circuit, but its precise value is not important. The closed-loop gain of the circuit is determined entirely by
, which we refer to as the open-loop gain, serves an important role in the circuit, but its precise value is not important. The closed-loop gain of the circuit is determined entirely by ![]() . (In the example below, we will examine the impact of different values of
. (In the example below, we will examine the impact of different values of ![]() on a circuit.)
on a circuit.)
Recall that the relationship between the error voltage and the output voltage is: ![]() from which we see that
from which we see that ![]() . Since
. Since ![]() is very large (ideally, infinite),
is very large (ideally, infinite), ![]() is very small (ideally, zero). From this information, we can make the following inference about the behavior of a feedback circuit such as this: the very large gain of the forward amplifier,
is very small (ideally, zero). From this information, we can make the following inference about the behavior of a feedback circuit such as this: the very large gain of the forward amplifier, ![]() combined with feedback amplifier gain
combined with feedback amplifier gain ![]() and a difference-forming circuit results in a gain of
and a difference-forming circuit results in a gain of ![]() independent of
independent of ![]() . An important point is that the forward amplifier
. An important point is that the forward amplifier ![]() is prevented from saturating due to the feedback mechanism which drives the error voltage toward zero.
is prevented from saturating due to the feedback mechanism which drives the error voltage toward zero.
Example: in the previous problem, assume ![]() , and
, and ![]() . Assume the circuit is powered by a 12 volt unipolar source. Does the amplifier saturate? Why or why not? Determine
. Assume the circuit is powered by a 12 volt unipolar source. Does the amplifier saturate? Why or why not? Determine ![]() and
and ![]() as well as the closed loop gain of the amplifier,
as well as the closed loop gain of the amplifier, ![]() . Repeat for
. Repeat for ![]() .
.
Solution: For ![]() , the closed loop gain,
, the closed loop gain, ![]() . For an input
. For an input ![]() volt, the output voltage
volt, the output voltage ![]() ≈10 V. The error voltage in this case is
≈10 V. The error voltage in this case is ![]() . The forward amplifier
. The forward amplifier ![]() does not saturate, since the product
does not saturate, since the product ![]() indicating that the output voltage is kept below the
indicating that the output voltage is kept below the ![]() volt power supply rail and the amplifier
volt power supply rail and the amplifier ![]() is operated in its linear region.
is operated in its linear region.
For ![]() , the closed loop gain,
, the closed loop gain, ![]() . The output voltage
. The output voltage ![]() . The error voltage is
. The error voltage is ![]() . The forward amplifier does not saturate because the output voltage is kept below the power supply rail.
. The forward amplifier does not saturate because the output voltage is kept below the power supply rail.
Now let us take the previous discussion and apply to to the op amp circuit that has a feedback resistor connecting ![]() to
to ![]() .
.

We are interested in deriving the input – output relationship for this circuit, ![]() vs
vs ![]() , from which, we will determine the closed-loop gain,
, from which, we will determine the closed-loop gain, ![]() . We use the equivalent circuit shown to analyze this circuit using circuit analysis rules. The equivalent circuit replaces the op amp’s “triangle” symbol with a dependent source at the output, and we assume infinite input resistance and zero output resistance. This model is only valid when the op amp is operated within its linear region of operation (ie, it is not saturated); so we will need to verify that voltage levels are kept within this region.
. We use the equivalent circuit shown to analyze this circuit using circuit analysis rules. The equivalent circuit replaces the op amp’s “triangle” symbol with a dependent source at the output, and we assume infinite input resistance and zero output resistance. This model is only valid when the op amp is operated within its linear region of operation (ie, it is not saturated); so we will need to verify that voltage levels are kept within this region.
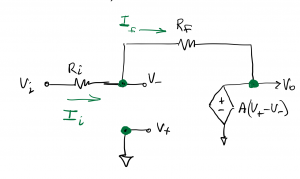
The input voltage to this circuit, Vi, is known and the other node voltages, V–, V+, and Vo, need to be determined. We can use the technique of node voltage analysis to determine these voltages. We can see that
(9) ![]()
since the non-inverting terminal is connected directly to a ground node. Since Vo is connected directly to the + terminal of the dependent voltage source, and since V+=0, we have
(10) ![]()
Now we apply KCL at node V– as we practiced when studying node voltage analysis:
(11) ![]()
(12) ![]()
substituting ![]() we have
we have
(13) ![]()
which gives, after some algebra,
(14) ![]()
The closed-loop gain of the overall resulting circuit,
(15) ![]()
since ![]() is large, we can ignore terms involving
is large, we can ignore terms involving ![]() to obtain an approximate expression for closed loop gain,
to obtain an approximate expression for closed loop gain,
(16) ![]()
Note this this expression for ![]() is exact when we have an ideal op amp with
is exact when we have an ideal op amp with ![]() .
.
The differential input signal is related to the output voltage by
(17) ![]()
Rearranging, we see that
(18) ![]()
and with ![]() very large (ideally, zero), the differential input voltage
very large (ideally, zero), the differential input voltage
(19) ![]()
and, when ![]() , the approximation becomes an equality. This is due to the presence of the feedback resistor connecting
, the approximation becomes an equality. This is due to the presence of the feedback resistor connecting ![]() to
to ![]() . Although we have developed this result and observation in the case of the particular negative feedback Op Amp circuit shown in figure 6.24, the results here do apply for all negative feedback op amp circuits. This result leads to an important observation that negative feedback in an Op Amp circuit causes the differential input voltage to become negligible. This observation, referred to as the Summing Point Constraint, or Virtual Short Circuit, leads to a quick and simple way to analyze negative feedback op amp circuits, namely:
. Although we have developed this result and observation in the case of the particular negative feedback Op Amp circuit shown in figure 6.24, the results here do apply for all negative feedback op amp circuits. This result leads to an important observation that negative feedback in an Op Amp circuit causes the differential input voltage to become negligible. This observation, referred to as the Summing Point Constraint, or Virtual Short Circuit, leads to a quick and simple way to analyze negative feedback op amp circuits, namely:
-
- confirm the presence of a negative feedback path between
 and
and 
- apply the summing point constraint:
- recall that the input currents flowing into the + and – terminals of the op amp are negligible.
- confirm the presence of a negative feedback path between
We can apply this technique to the analysis of the inverter circuit that we examined above:
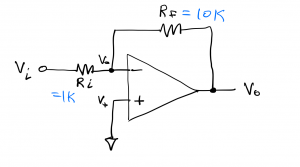
Since there is negative feedback, via ![]() , the summing point constraint tells us that V–=V+. Since the non-inverting terminal of the op amp is connected to ground, we have
, the summing point constraint tells us that V–=V+. Since the non-inverting terminal of the op amp is connected to ground, we have
(20) ![]()
Applying KCL at the op amp inverting input terminal, we have
(21) ![]()
where ![]() is the current through
is the current through ![]() and
and ![]() is the current through
is the current through ![]() . By Ohm’s law, we can write
. By Ohm’s law, we can write
(22) ![]()
which simplifies to
(23) ![]()
and gives us the gain of the amplifier circuit,
(24) ![]()
Examples
Example: Determine the closed-loop gain of the op amp circuit shown assuming ![]() . Determine voltages
. Determine voltages ![]() , as well as currents
, as well as currents ![]() and
and ![]() , assuming an input voltage
, assuming an input voltage ![]() volts and assuming the op amp is powered by a
volts and assuming the op amp is powered by a ![]() unipolar supply voltage.
unipolar supply voltage.
Solution: From above, we have the closed loop gain of the circuit, ![]() .
.

![]() since this input is connected directly to ground,
since this input is connected directly to ground,
![]() via the summing point constraint, which gives
via the summing point constraint, which gives ![]() for negative feedback circuits.
for negative feedback circuits.
![]() volts
volts
![]() mA.
mA.![]() mA
mA

