Linearizing Data with Algebra

Plotting strange combinations of variables

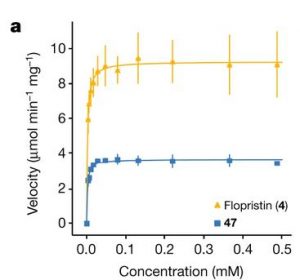
As described in the Introduction to this lab, while many relationships in nature are linear, many others are not. However, as discussed in a prior lab, linear fits have the advantage that they are easy for our ape-brains to comprehend. Moreover, the fit to a line only has two parameters: the slope and the intercept which makes it easy to understand how the fit is done in terms of the residuals etc. Can we use the benefits of linear fits for non-linear data? The answer (of course given the title of this lab), is yes! One way to do this is by simply plotting combinations of variables on each axis instead of simple things like time or distance. For example in figure 3a from Q. Li et al.[1] we see \frac{ \mathrm{\mu mol} }{ \mathrm{min} \, \mathrm{mg} } plotted on the vertical axis. Sometimes, by choosing the correct set of axes, you can make data that is not a line into a line.

Summary of VatA acetylation kinetics and in vitro inhibition of the E. coli ribosome by 4 and 47. Error bars denote s.d. (3 technical replicates).
Figure 3a: Summary of VatA acetylation kinetics and in vitro inhibition of the E. coli ribosome by 4 and 47. Error bars denote s.d. (3 technical replicates).

Example from Quantum Mechanics and Chemistry with which you should be familiar

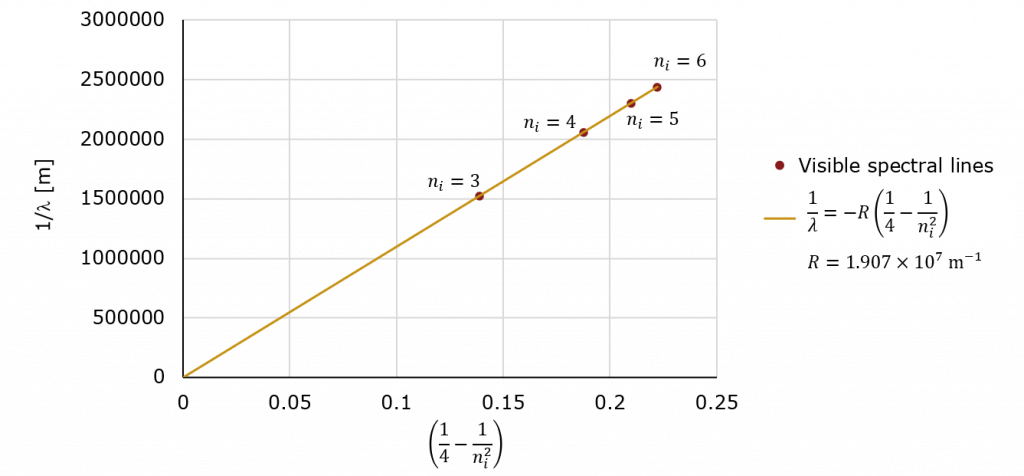
In Chemistry and our Unit on Quantum Mechanics, we discussed the atomic spectrum of hydrogen the visible spectral lines of which (the so-called Balmer series) are shown below.

Visible lines in the hydrogen emission spectrum.

We solved for these wavelengths using conservation of energy:

\Delta E = Q + W

E_f - E_i = E_\gamma

For hydrogen, the energy levels are given by E_n = \frac{-Rhc}{n^2} while the energy of the photon \gamma is given by the familiar formula E_\gamma = \frac{hc}{\lambda}. The result is

-Rhc \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right) = \frac{hc}{\lambda}

For the visible lines, n_f is always equal to 2 leaving us with

-Rhc \left( \frac{1}{2^2} - \frac{1}{n_i^2} \right) = \frac{hc}{\lambda}

-Rhc \left( \frac{1}{4} - \frac{1}{n_i^2} \right) = \frac{hc}{\lambda}

Dividing across by hc we have

\frac{1}{\lambda} = -R \left( \frac{1}{4} - \frac{1}{n_i^2} \right)

While this may not look like it, it is the equation for a line! All we need to do is plot \left( \frac{1}{4} - \frac{1}{n_i^2} \right) (which is unit-less) on the horizontal and \frac{1}{\lambda} on the vertical (in units of 1/m) and the slope will be R = 1.097 \times 10^7 \, \mathrm{m}^{-1} with an intercept of zero!

plot 1/4 - 1/n vs 1/lambda to get the Rydberg as the slope

 

Key Takeaways

Sometimes, by plotting seemingly strange combinations of variables you can convert a non-linear relationship into a linear one!

  1. Li, Qi, Jenna Pellegrino, D. John Lee, Arthur A. Tran, Hector A. Chaires, Ruoxi Wang, Jesslyn E. Park, et al. “Synthetic Group A Streptogramin Antibiotics That Overcome Vat Resistance.” Nature 586, no. 7827 (October 2020): 145–50. https://doi.org/10.1038/s41586-020-2761-3 . ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Physics 132 Lab Manual by Brokk Toggerson and Aidan Philbin is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book