How to write numbers – significant figures
If you look in any scientific article, you will see that results are written in the form 0.17 ± 0.02, i.e. some plus-or-minus its associated uncertainty.
Key Takeaways
Throughout this sequence of labs, you will generally be expected to write your numbers in this standard form of a central value plus-or-minus an associated uncertainty.
The central value is almost always the mean of the data (occasionally, people will use some other statistic, but in this class, it will always be the mean). Exactly how the uncertainty, on the other hand, is calculated can vary depending on the context. One way to define the uncertainty is through the use of the significant figures you have just reviewed.
In the case of significant figures, you already know how to determine how many digits to keep when writing the central value: simply use the significant figures rules to which you are accustomed. To determine what value to put after the 
we need to think about the meaning behind significant figures. Significant figures imply that the last digit is the uncertain one. Thus, the uncertainty is one unit of that digit. Let’s reconsider the example of the graduated cylinder in Review of Significant Figures to see this in action.
Example of the graduated cylinder
To measure the volume of liquid in this graduated cylinder, you must mentally subdivide the distance between the 21 and 22 mL marks into tenths of a milliliter, and then make a reading (estimate) at the bottom of the meniscus.
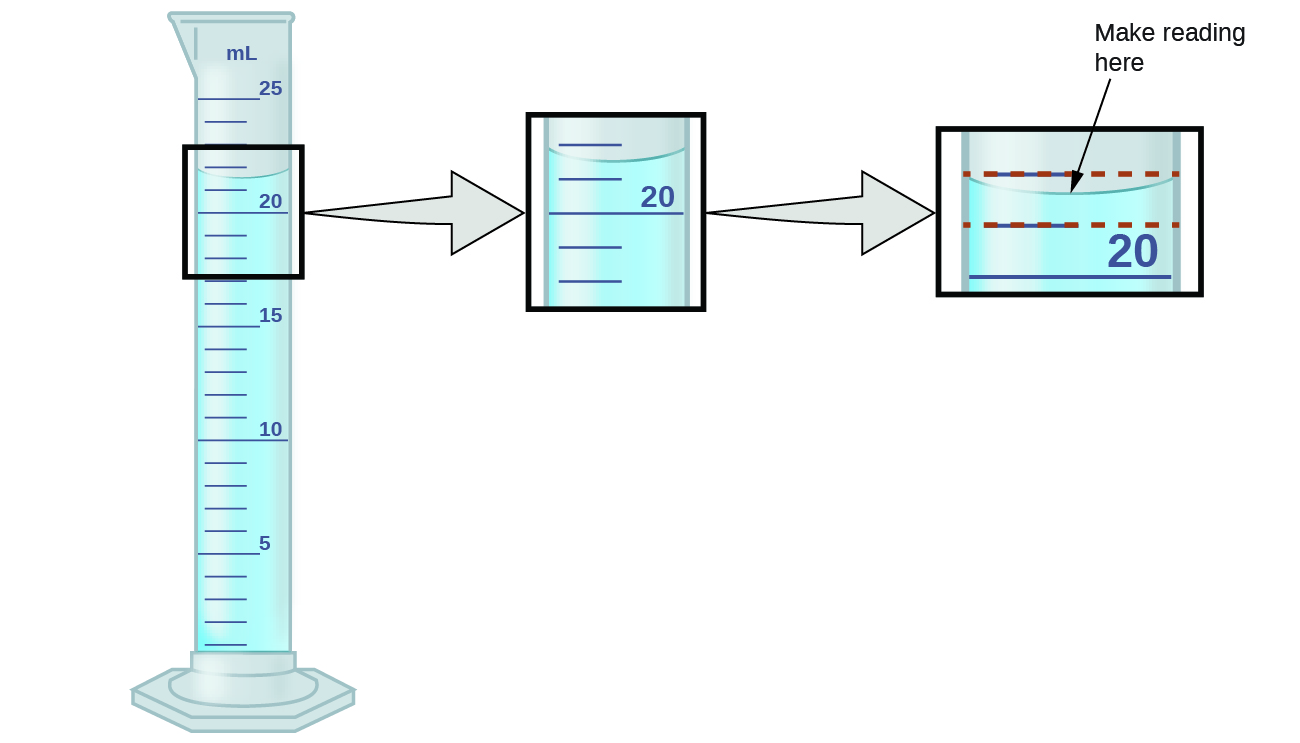
Refer to the illustration in (Figure). The bottom of the meniscus in this case clearly lies between the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL but less than 22 mL. The meniscus appears to be a bit closer to the 22-mL mark than to the 21-mL mark, and so a reasonable estimate of the liquid’s volume would be 21.6 mL. In the number 21.6, then, the digits 2 and 1 are certain, but the 6 is an estimate. Some people might estimate the meniscus position to be equally distant from each of the markings and estimate the tenth-place digit as 5, while others may think it to be even closer to the 22-mL mark and estimate this digit to be 7.
Clearly the significant figures rules assume an uncertainty of 0.1 mL. Thus, writing this measurement as a central value an uncertainty, we would say: 
The value for your data. Usually the mean, but occasionally something else.
