Determining the Uncertainty on the Intercept of a Fit

Brokk Toggerson

We have talked about how to fit data in such a way as to include the uncertainties in the vertical direction. The results of that procedure yields a slope m_{\rm weighted} with its uncertainty \sigma_{m_{\rm weighted}} straight from the results of the spreadsheet LINEST function. We also saw how to use this corrected slope and the average x, \bar{x}, and average y, \bar{y}, to determine the intercept of the weighted fit:

b_{\rm weighted} = \bar{y} - m_{\rm weighted} \bar{x}

How do we get the uncertainty on that intercept 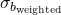\sigma_{b_{\rm weighted}}? Monte Carlo!

In this case, we treat \bar{x} and \bar{y} as without uncertainty. Only the slope m_{\rm weighted} has the uncertainty \sigma_{m_{\rm weighted}} reported by LINEST. The procedure is then:

  1. Draw a trial value of 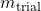m_{\rm trial} from a normal distribution with mean equal to the slope from LINEST and standard deviation equal to the LINEST result: NORM.INV(RAND(), m_{\rm weighted}, \sigma_{m_{\rm weighted}}).
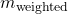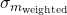  2. Use that 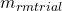m_{rm trial} to calculate a trial intercept b_{\rm trial} = \bar{y} - m_{\rm trial} \bar{x}.
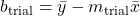  3. Repeat this a bunch of times.
  4. Determine the standard deviation of your trials.

That’s it! Same procedure as we have used in a couple different circumstances now!

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Physics 132 Lab Manual by Brokk Toggerson is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book