Introduction to Linearizing with Logarithms

Brokk Toggerson

Introduction

In a previous lab, you used algebra to linearize data: you just moved variables around to make something that wasn’t a line look like a line so that you could fit it. While this is a common way of linearizing data, a far more common approach is to use logarithms. Logarithms can also be used to linearize data and are seen throughout the literature in the form of log-lin plots, where instead of plotting y vs. x, one plots the logarithm of y vs x, and log-log plots, where the logarithm of y is plotted against the logarithm of x.

Log-Lin Plots

For example, when I plot the number of COVID-19 cases in the US in March 2020 according to the WHO, the result is an exponential looking curve.

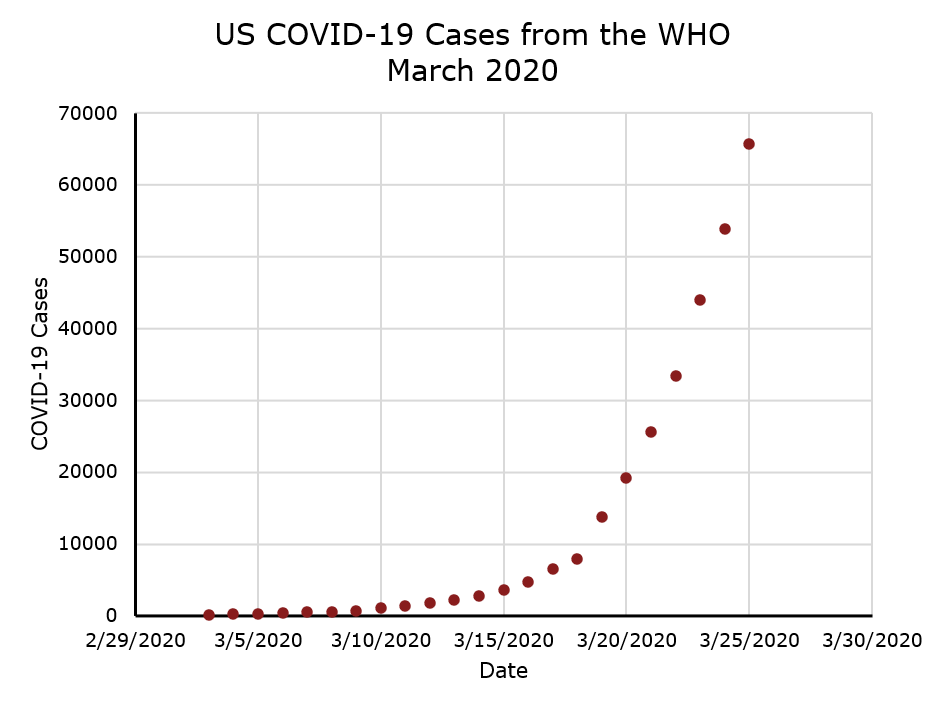
US COVID-19 Cases in March 2020 according to the WHO are exponential

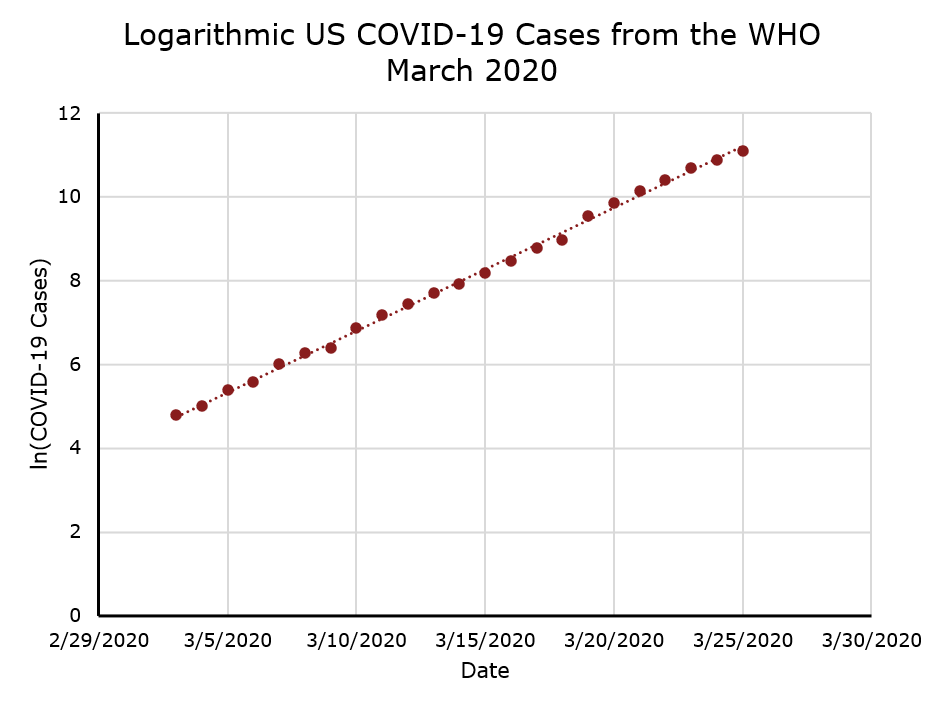
However, if I plot the natural logarithm (ln) of the number of cases on the vertical axis instead, the result is a straight line, and we know how to fit those!

Natural logarithm of the number of COVID-19 Cases in the US March 2020 according to WHO is linear

Log-Log Plots

Another example is so-called Kleiber’s Law which is an empirical relationship between  metabolic rate of organisms P and their mass M

P = a M^b

where a is a constant and b is the power. Thommen et al [1] looked at this relationship in planarians (flatworms). The result is shown below along with an ordinary least fit line. You can see that the data are not exactly linear.

Metablolic rate [uW] vs. planarian mass [mg] follows a non-linear relationship

However, when, as is done in the paper, the data are plotted logarithmically, this time on both the horizontal and vertical axes, the result is a line.

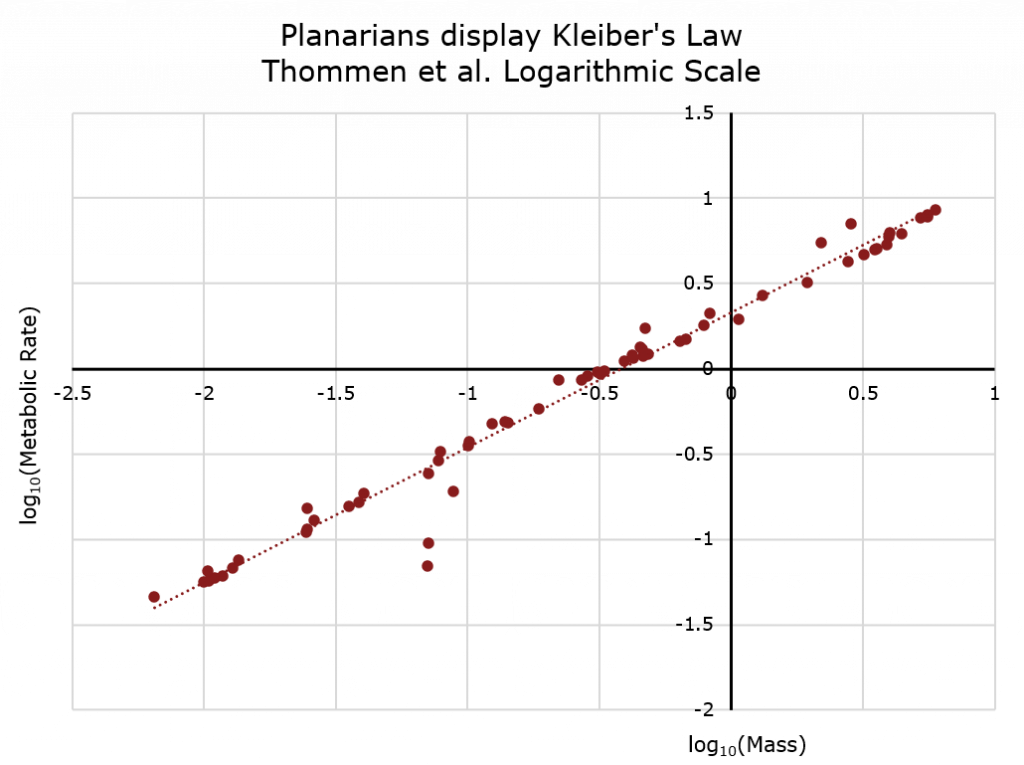
Metabolic rate as a function of mass plotted on logarithmic scales is a linear relationship

Due to the properties of logarithms (reviewed in a later section), the slope of this line is the power b and the intercept is b \log ( a ). It turns out, for reasons not completely understood, that the power b \approx 0.75 for a large range of species from bacteria to humans as seen in their figure 1D shown below and described more in A. Makarieva et al [2].

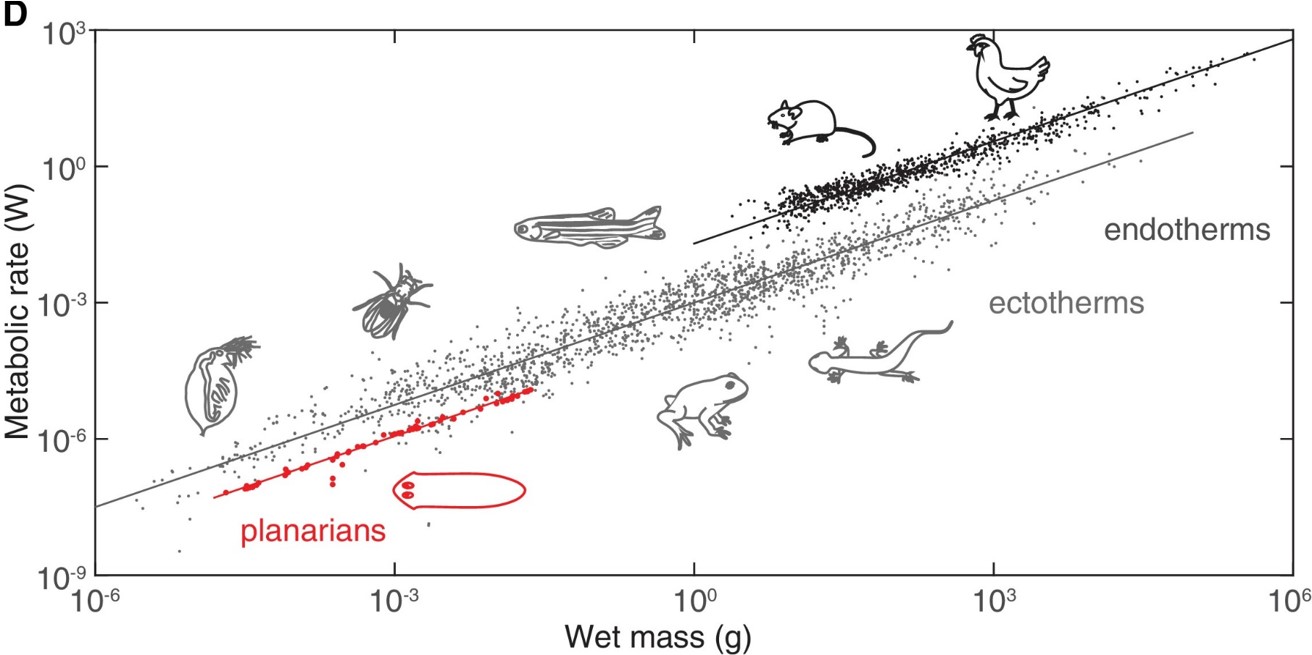
Kleiber's Law holds for a wide range of species with basically the same power b of about 0.75

Clearly logarithms are used extensively in the scientific literature to linearize data. This lab will explore how to use logarithms to understand more complex data.

  1. Thommen, Albert, Steffen Werner, Olga Frank, Jenny Philipp, Oskar Knittelfelder, Yihui Quek, Karim Fahmy, et al. “Body Size-Dependent Energy Storage Causes Kleiber’s Law Scaling of the Metabolic Rate in Planarians.” eLife. eLife Sciences Publications Limited, January 4, 2019. https://doi.org/10.7554/eLife.38187. ↵
  2. Makarieva, Anastassia M., Victor G. Gorshkov, Bai-Lian Li, Steven L. Chown, Peter B. Reich, and Valery M. Gavrilov. “Mean Mass-Specific Metabolic Rates Are Strikingly Similar across Life’s Major Domains: Evidence for Life’s Metabolic Optimum.” Proceedings of the National Academy of Sciences 105, no. 44 (November 4, 2008): 16994–99. https://doi.org/10.1073/pnas.0802148105. ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Physics 132 Lab Manual by Brokk Toggerson is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book