A brief overview of Slope and it’s units

Slope, or m as we often write it in equations, describes the way a function changes. The slope of a function y(x) is the change in y divided by the change in x:

(1)  m = Δy/Δx

Linear graphs are graphs of straight lines, and can be defined by their slope, m, and their y-intercept, b:

(2) y(x) = m*x + b

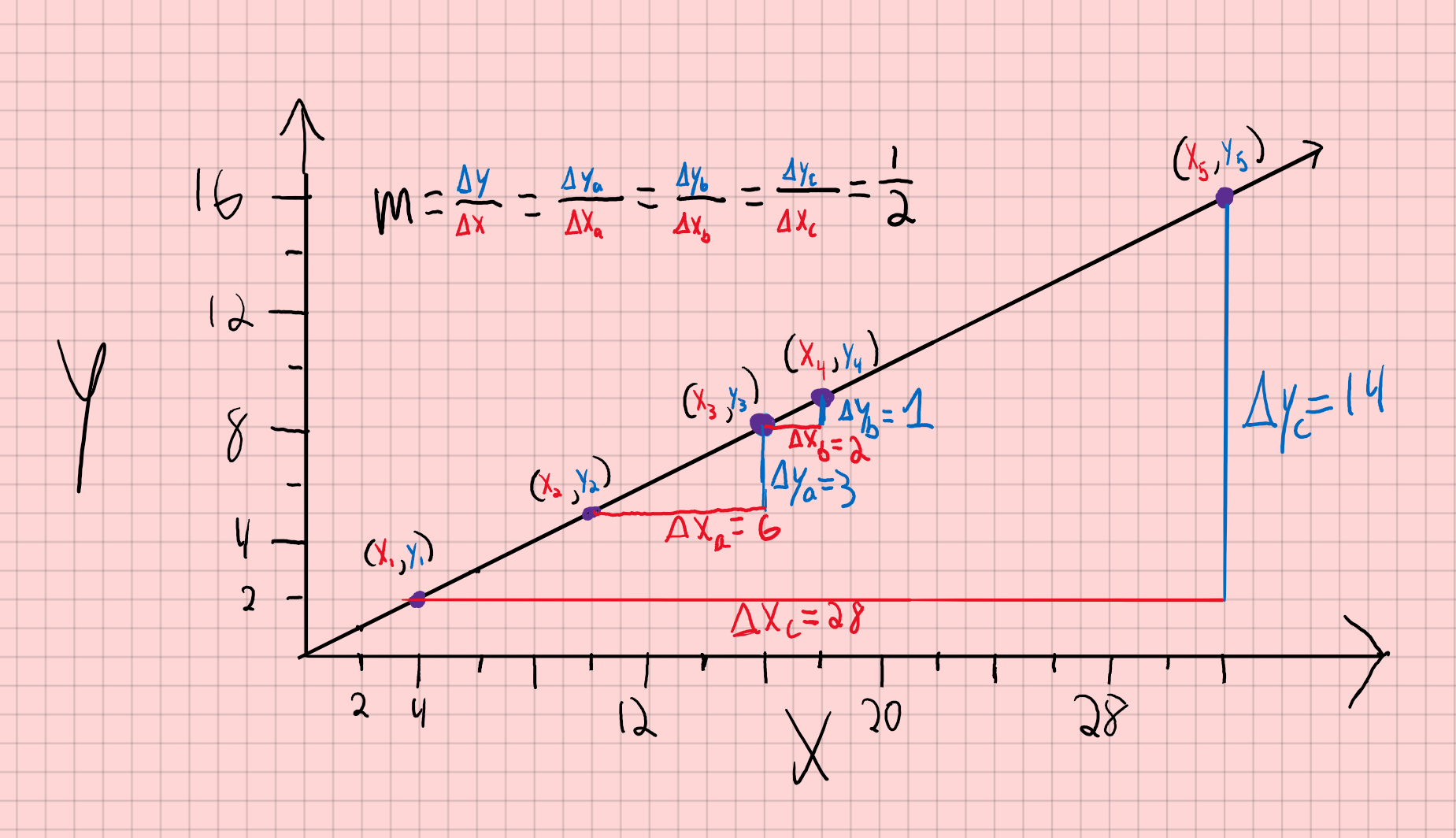
In the figure below, there is a linear function plotted on a graph. If we want to find the slope of this function, we must choose two points on the line, and use Equation (1). Let’s use (x₂, y₂) and (x₃, y₃). We will have:

m = Δy_a/Δx_a = (y₃-y₂)/(x₃-x₂) = 3/6=1/2

Because this function is linear, we find the same slope using any two points, as shown below.

Alright so we know how to interpret the slope of a line as it’s rate of change, but what would the units of slope be? Let’s work trough a word problem to sort it out.

A runner runs for different time intervals, and records how far they run each time. They produce the scatter plot below, and fit a line to it to find the slope. What exactly are they finding? What are the units?

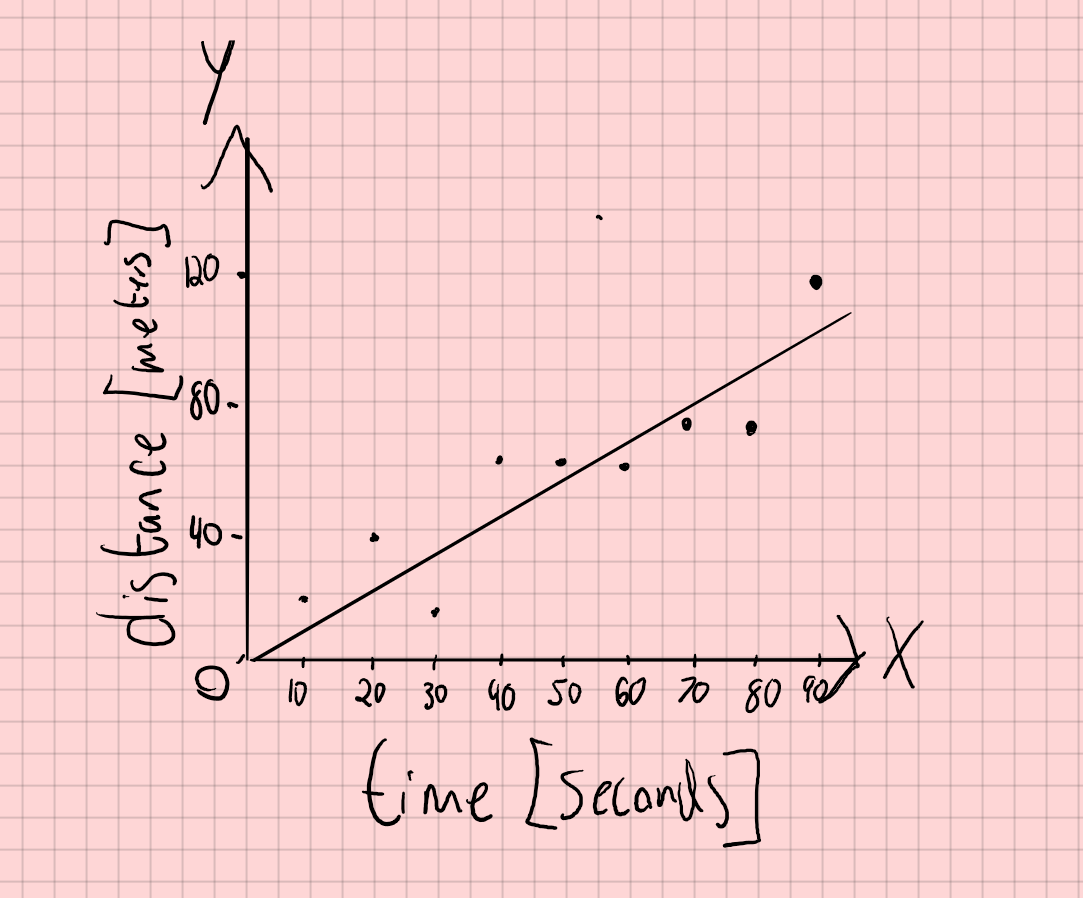
So if they’re calculating slope, they’re using Equation (1): m = Δy/Δx. Looking at the plot, the y-axis has units of distance and the x-axis has units of time, so m = Δy/Δx = Δdistance/Δtime. We recognize distance/time as velocity. Because this is a line of best fit, the slope is the average velocity of the runner. So for the units, in this plot slope has units of meters/second.

Generally:

units of slope=(units of y)/(units of x)