Introduction to Fields

For the past few units we have been really focusing on the ideas of light, now, everything we’ve been talking about in our units on geometric optics and physical optics applies to matter waves as well. We’ve just really been focusing on the applications to light. Now here in Unit 3, we will return two electrons, and these will be the focus of our attention for the next two units. Up to now, we’ve been ignoring the fact that electrons have charge, and we know that they do, so it’s time to fix that. By thinking about the charge attribute of electrons we will begin our study of the electric force.

To begin, I want to remind you from 131 that there are fundamentally only four forces: The strong nuclear force, which is responsible for holding all of the positively charged protons in the nucleus together. The electrical and magnetic forces, which we will see through this course are really two deeply connected sides of the same coin, and these are the ideas of opposite charges attract like charges repel and magnets.

Next in strength we have the weak nuclear force responsible for radioactive decay, and then finally the gravitational force, which holds you to the Earth and holds the Earth in orbit around the Sun.

Gravity was talked about in some depth in Physics 131, whereas electricity and magnetism will consume our attention for the rest of 132. It’s worth pointing out that the idea of opposite charges attract and like charges repel is the fundamental origin of all of the other forces taught in these courses. For example, in 131, you discuss the normal force, when a physics book sits on a table you have the weight of the book, but you also have a normal force from the table on the book, which keeps it from falling through the table. This force is perpendicular, or normal, to the surface between the table in the book and really arises because of the electrons in the table repelling the electrons in the book.

Another force discussed in 131 is the idea of tension. For example, when a block is just hung by a string, you have the weight of the block being countered by the tension in the rope, but where does this tension ultimately come from? This tension comes from the atomic bonds which are fundamentally the electrical attraction between one molecule of rope and the next. Similarly, the spring force and Hooke’s law are a result of atomic bonds, which are electrical at the microscopic scale. Finally, the frictional forces arise from Van der Waals interactions between the molecules and different surfaces. Once again, you’re talking about the electrical interactions between atoms.

Before we begin with the electric field we’re going to explore everyone’s favorite number from Physics 131, this

that was used extensively in that course, and we’re going to deconstruct exactly what this number is. Gravity is a bit more familiar to us, as we experience it on a daily basis. And we will build up the idea of the electric field in parallel, using gravity as a crutch.

Absolutely everything in the universe experiences gravity. We saw in class, through our gravitational redshift of light, that even light experiences gravity. However only those objects with charges will experience electrical forces. Can you perhaps think of something that experiences gravity but not electricity? You would need something that has mass but not an electric charge.

Let’s begin thinking about gravity. We know that the force of gravity is what holds the moon in orbit around the Earth, but how does the moon know that the Earth is there? I mean the moon is meters away from the Earth. That’s a long way. How does the moon know that the Earth is even there? To simplify and bring it a little more down to Earth, no pun intended, we’re going to think about a ball. We all know that when I release a ball it falls due to the Earth’s gravity. We could ask the same question; how does the ball know that the Earth is there? They’re not in contact. Yes, the distances are a lot smaller, but they don’t touch each other. How does the ball know that the Earth is there?

The way that this is explained is that the Earth generates a gravitational field and this gravitational field is what the letter from Physics 131 represents, and the strength of that gravitational field is Newton’s per kilogram. Now you might be used to thinking about it being meters per second squared but if you look a little bit at Newton’s second law, , you will see that meters per second squared and Newton’s per kilogram are equivalent units. We’re going to think in terms of Newton’s per kilogram, because it’s a more useful unit for our purposes right now.

The Earth generates this gravitational field and it points straight down and it has a magnitude of Newton’s per kilogram. Now you will notice that the ball does actually touch the Earth’s gravitational field, it doesn’t touch the Earth, but it does touch this gravitational field. And through this contact the ball reacts to that field by feeling a gravitational force, . The force is the mass of the ball, , times the strength of the gravitational field, . That’s what gives rise to the force.

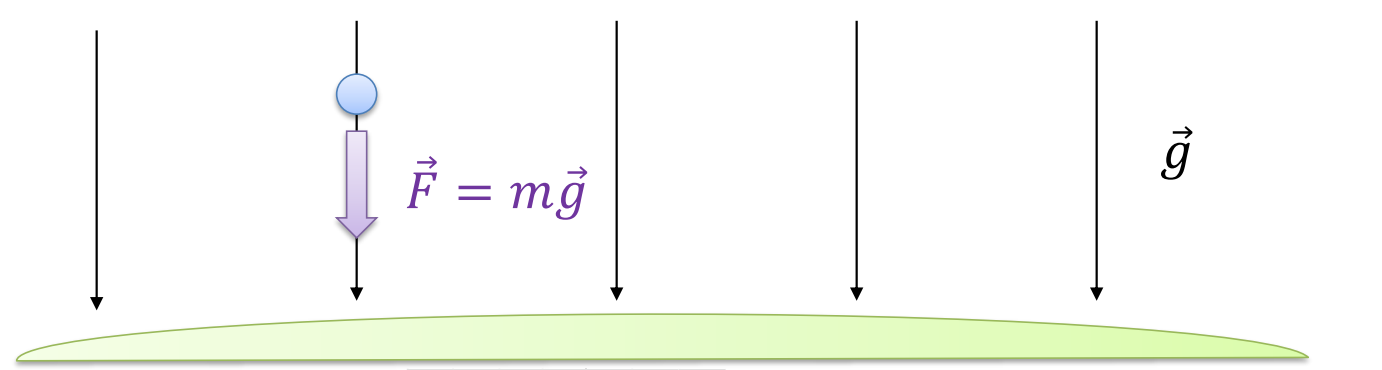
Now let’s return to these units for , these Newton’s per kilogram that you might not be used to thinking about. For every one kilogram of ball, the ball feels 9.8. Newton’s of force. That’s what means, a two-kilogram ball will feel 2 times 9.8 Newton’s of force. That’s why these units are somewhat useful for our purposes right now, is it tells us how many Newton’s of force we get for each kilogram of ball, that’s what 9.8 represents.

Why did we introduce this middle step of a gravitational field that’s invisible and extends from the Earth? Why did we invent this? Why can’t we just say that something causes the ball to fall and the magnitude of the force is ? That’s what we did in 131.

Well the reason we invent this is because this field, while we cannot see, it is a fundamentally real object. It’s just as real as a ball. Yes, it’s invisible, but so are atoms, and you believe atoms are real so the field is a similar thing. It is fundamentally a real quantity, it contains energy, in fact we can think about the energy when we let the ball go. When the ball falls it gains kinetic energy, where does that energy come from? That energy comes from the gravitational field. This is a fundamentally different way of thinking a little more deeply about what gravity actually is and where this Newton’s per kilogram number comes from.

Now let’s return to the idea of electricity, the main focus of our course. How does the electron know the nucleus is there? We know that it’s the positively charged nucleus attracting the negatively charged electron that holds the atom together. But again, the nucleus and the electron do not touch, so how does the nucleus know that the electron is there? We’re going to add a proton to this situation for purposes of illustration, but the same argument can be made. How does this stray proton know that the nucleus is there?

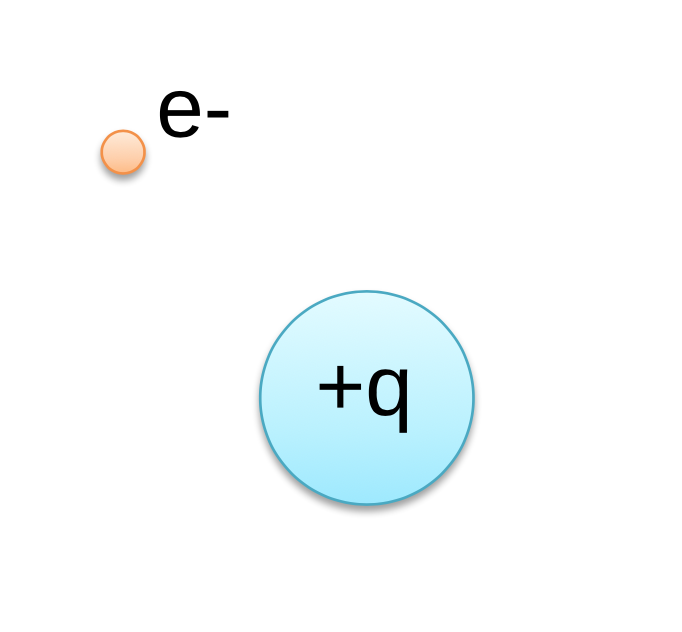
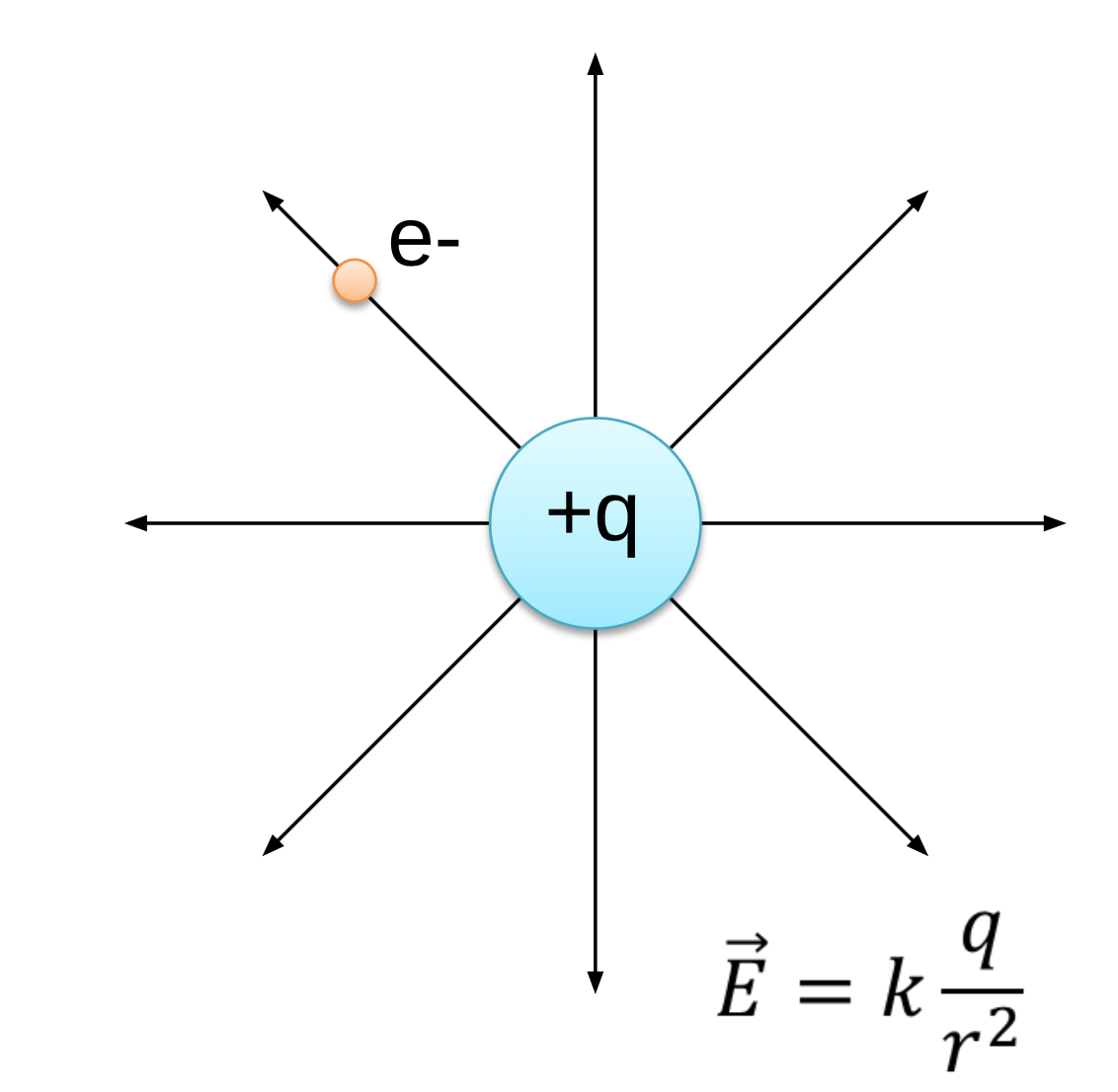
Well, we use the same sort of idea, the nucleus generates an electric field that we call and then the other charges, this electron and striped proton, respond to that field by feeling a force.

The force felt by the electron is and, with analogy to gravity, where the force was the mass times the gravitational field, the force felt by these other charges is going to be the charge times the electric field. The stray proton feels a force , where is the positive charge of proton, and similarly the electron also feels a force , where now this is the charge of the electron.

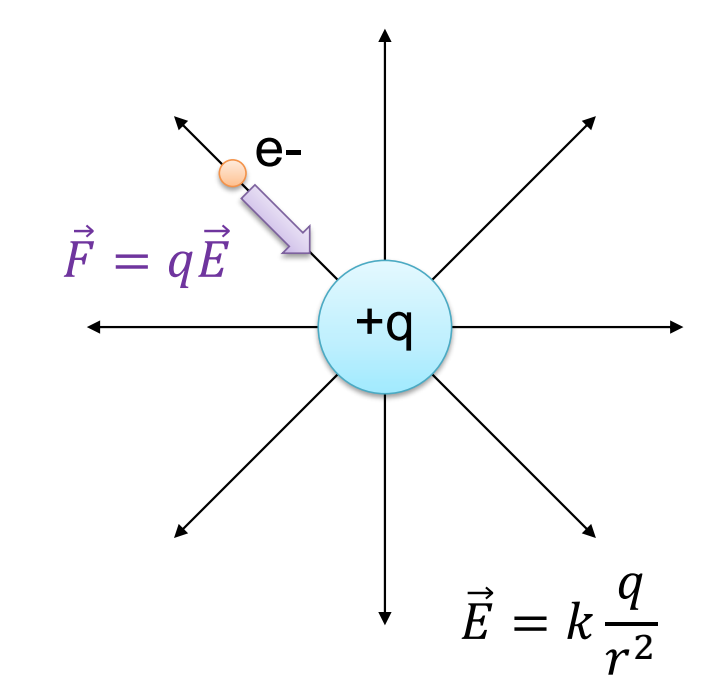
Now it’s worth noting that this expression gets the sign correct in the case of the proton. The charge is positive, and the force and the electric field are in the same direction. For the electron, the charge is negative and so the force and the electric field are in opposite directions, the force is inward, and the electric field is outwards. So, it’s important to keep in mind that this expression actually does get the signs correct, in fact so does our expression for gravity, mass is always positive and so the force of gravity is always in the same direction as the gravitational field. Once we know the forces we can then go on to calculate accelerations using Newton’s second law.