33 Sources of Magnetic Fields

Magnetic Fields Produced by Currents: Ampere’s Law

Derived from Magnetic Fields Produced by Currents: Ampere’s Law by OpenStax

Instructor’s Note

 

As before, I am NOT expecting you to fully understand everything in this section. I hope you:
  • Are reminded that moving charges (i.e. currents) are ultimately the source of all magnetic fields
  • Are reminded that magnetic field lines travel in closed loops
  • How to calculate the magnitude of the magnetic field some distance from a straight wire

How much current is needed to produce a significant magnetic field, perhaps as strong as the Earth’s field? Surveyors will tell you that overhead electric power lines create magnetic fields that interfere with their compass readings. Indeed, when Oersted discovered in 1820 that a current in a wire affected a compass needle, he was not dealing with extremely large currents. How does the shape of wires carrying current affect the shape of the magnetic field created? We noted earlier that a current loop created a magnetic field similar to that of a bar magnet, but what about a straight wire or a toroid (doughnut)? How is the direction of a current-created field related to the direction of the current? Answers to these questions are explored in this section, together with a brief discussion of the law governing the fields created by currents.

Magnetic Field Created by a Long Straight Current-Carrying Wire: Right Hand Rule 2

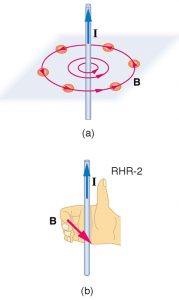
Magnetic fields have both direction and magnitude. As noted before, one way to explore the direction of a magnetic field is with compasses, as shown for a long straight current-carrying wire in Figure 1. Hall probes can determine the magnitude of the field. The field around a long straight wire is found to be in circular loops. The right hand rule 2 (RHR-2) emerges from this exploration and is valid for any current segment—point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops created by it.

Figure 1. (a) Compasses placed near a long straight current-carrying wire indicate that field lines form circular loops centered on the wire. (b) Right hand rule 2 states that, if the right hand thumb points in the direction of the current, the fingers curl in the direction of the field. This rule is consistent with the field mapped for the long straight wire and is valid for any current segment.

The magnetic field strength (magnitude) produced by a long straight current-carrying wire is found by experiment to be

B = \frac{\mu_{0} I}{2 \pi r} \text{(long straight wire)}

Instructor’s Note

 

I would like you to be able to use the equation above to get a numerical value.

where I is the current, r is the shortest distance to the wire, and the constant \mu_{0} = 4 \pi \times 10^{-7} \text{ T} \cdot \text{ m/A} is the permeability of free space. (\mu_{0} one of the basic constants in nature. We will see later that \mu_{0} is related to the speed of light.) Since the wire is very long, the magnitude of the field depends only on distance from the wire r, not on position along the wire.

Calculating Current that Produces a Magnetic Field

Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth’s at a distance of 5.0 cm from the wire.

Strategy

The Earth’s field is about 5.0 \times 10^{-5} \text{ T} and so here B due to the wire is taken to be 1.0 \times 10^{-4} \text{ T}. The equation B = \frac{\mu_{0} I}{2 \pi r} can be used to find I, since all other quantities are known.

Solution

Solving for I and entering known values gives

I = \frac{2 \pi r B}{/mu_{0}} = \frac{2 \pi (5.0 \times 10^{-2} \text{ m})(1.0 \times 10^{-4}\text{ T})}{4 \pi \times 10^{-7} \text{ T} \cdot \text{m/A}}

25 \text{ A}

Discussion

So a moderately large current produces a significant magnetic field at a distance of 5.0 cm from a long straight wire. Note that the answer is stated to only two digits, since the Earth’s field is specified to only two digits in this example.

Ampere’s Law and Others

The magnetic field of a long straight wire has more implications than you might at first suspect. Each segment of current produces a magnetic field like that of a long straight wire, and the total field of any shape current is the vector sum of the fields due to each segment. The formal statement of the direction and magnitude of the field due to each segment is called the Biot-Savart law. Integral calculus is needed to sum the field for an arbitrary shape current. This results in a more complete law, called Ampere’s law, which relates magnetic field and current in a general way. Ampere’s law in turn is a part of Maxwell’s equations, which give a complete theory of all electromagnetic phenomena. Considerations of how Maxwell’s equations appear to different observers led to the modern theory of relativity, and the realization that electric and magnetic fields are different manifestations of the same thing. Most of this is beyond the scope of this text in both mathematical level, requiring calculus, and in the amount of space that can be devoted to it. But for the interested student, and particularly for those who continue in physics, engineering, or similar pursuits, delving into these matters further will reveal descriptions of nature that are elegant as well as profound. In this text, we shall keep the general features in mind, such as RHR-2 and the rules for magnetic field lines listed in Magnetic Fields and Magnetic Field Lines, while concentrating on the fields created in certain important situations.

Making Connections: Relativity

Hearing all we do about Einstein, we sometimes get the impression that he invented relativity out of nothing. On the contrary, one of Einstein’s motivations was to solve difficulties in knowing how different observers see magnetic and electric fields.

Section Summary

  • The strength of the magnetic field created by current in a long straight wire is given by

B = \frac{\mu_{0} I}{2 \pi r} \text{(long straight wire)},

where I is the current, ris the shortest distance to the wire, and the constant \mu_{0} = 4 \pi \times 10^{-7} \text{ T} \cdot \text{m/A} is the permeability of free space.

  • The direction of the magnetic field created by a long straight wire is given by right hand rule 2 (RHR-2): Point the thumb of the right hand in the direction of current, and the fingers curl in the direction of the magnetic field loops created by it.
  • The magnetic field created by current following any path is the sum (or integral) of the fields due to segments along the path (magnitude and direction as for a straight wire), resulting in a general relationship between current and field known as Ampere’s law.

Homework

13. Magnetic fields from power lines.

14. Magnetic fields in your car.

 

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book