4 Review of Conservation of Energy
Instructor’s Note
This unit, in fact this entire course, will spend a lot of time talking about energy: a topic covered extensively in Physics 131 as well as in your Biology and Chemistry courses. This chapter is therefore a bit different: we provide links to the relevant sections on energy from the Physics 131 textbook Forces, Energy, Entropy for your reference, with the key takeaways from each section. Just review what you need.
There are also a few homework problems at the end, just to make sure everyone is on the same page.
Relevant parts from Physics 131: Forces, Energy, Entropy:
- Unit IV – Chapter 2 Introduction: Introduction to Energy
- Unit IV – Chapter 2.1: Units of Energy
- Note, we will use the eV unit of energy described here much more in this class than in Physics 131.
- Unit IV – Chapter 2.2: Types of Energy and Scales of Energy
- It is important to think about the fact that there are fundamentally only two kinds of energy: potential and kinetic.
- Unit IV – Chapter 2.3: Conservation of Energy
- This is one of the fundamental of this unit (and all of physics). We will begin many problems with this idea.
- Unit IV – Chapter 2.4: Ways to Transfer Energy
- The key idea here is that there are two ways to transfer energy: and .
- Heat
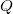is the transfer of energy through collisions at the microscopic scale. This includes , an idea that will appear in a later section of this reading. - Work is the application of a force for a distance
.
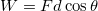- Unit IV – Chapter 2.5: The Formal Statement of the Conservation of Energy as the First Law of Thermodynamics
- The change in energy of a system
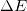is the amount going in or out as heat and work: 
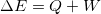. This is the principle from which we will begin many of our analyses.
- The change in energy of a system
- Unit IV – Chapter 3 Introduction: Energy of Objects as a Whole
- This is where the ideas of kinetic and potential energy as you saw them in 131 are introduced.
- Unit IV – Chapter 3.1: Kinetic Energy of an Object
- We will be looking a lot at the kinetic energies of electrons.
- Unit IV – Chapter 3.2: Examples Applying Conservation of Energy with only Kinetic Energy
- If you need to refresh how to use the kinetic energy formula
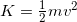
- If you need to refresh how to use the kinetic energy formula
- Unit IV – Chapter 3.3: Macroscopic Potential Energy
- This is where the idea of gravitational potential energy
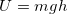is discussed. We will use this expression in this unit. - More importantly, we will build an understanding of electrical potential energy in Unit III partially by analogy and comparing and contrasting with gravity.
- The arbitrary nature of the definition of zero of potential energy discussed in this section will also be relevant, and may be worth review.
- This is where the idea of gravitational potential energy
- Unit IV – Chapter 4.1: The Potential Energy of Molecules
- The idea that two charges infinitely far apart have, by convention, zero potential energy will be relevant as will the idea that bonded electrons/atoms have negative potential energy.
- Unit IV – Chapter 4.2: Application of Bond Energies
- This is an example problem looking at negative bond energies
A Video Reviewing Problem Solving with Conservation of Energy
This example can be either watched or read
With what minimum speed must you toss a 
ball straight up to hit the 
meter high roof of a gymnasium if you release the ball 
above the ground? With what speed does the ball hit the ground?
You can use conservation of energy to solve this problem.
What is the initial energy state of the ball? We have some kinetic energy and some potential energy, so we have both. How do we know we have kinetic energy? Because we throw the ball, if the ball has no initial Kinetic energy which means it’s not moving that means it doesn’t go up, it had to have had some kinetic energy for it to actually go up and had to have some initial velocity when we threw it. Does it have any initial potential energy? The ball starts above the ground initially, this tells me it started out with some potential energy, it’s already above the ground.
What is its final energy state in the perfect world in physics land? Does it have Kinetic energy at the roof? No, we’re assuming it just touches the roof and has zero velocity at the roof for that moment in time, so its kinetic final energy is actually zero. All we have left is potential final energy.
What speed does it hit the ground? Energy initial equals energy final, what’s the initial energy state? My initial is the ball at the top of the ceiling. My final is just before it hits the ground. How fast does it hit the ground? It started from the roof, falls down. What is the energy state at the roof? It’s all potential. What’s the energy state the moment before it hits the ground? It’s lost all its potential energy, and its converted into kinetic energy.
Your friends Frisbee has become stuck 26 meters above the ground in a tree. You want to dislodge the Frisbee by throwing a rock at it. The Frisbee is stuck pretty tight, so you figure the rock needs to be traveling at least 5.4m/s when it hits the Frisbee. If you release the rock 1.6 meters above the ground, with what minimum speed must you throw it?
Energy initial has to equal energy final, what is my initial state of affairs? When I’m throwing the rock, that’s my initial state of affairs. Do I have kinetic energy in the beginning? I must have it. How do I know I must have kinetic energy? Because I’m throwing the rock, so the rock has to have some initial velocity. Do I have any initial potential energy? Yes, because I started 1.6 meters above the ground. What’s my final state of affairs? Do I have any kinetic energy at the end? When the rocks up there at the frisbee, does it have any kinetic energy? I know that it had to have a velocity, 5.4m/s, I know that the moment before I hit the frisbee I had to have this velocity. Therefore, I know I had some kinetic energy up there. Do I have any final potential energy? Yes, because it is up in the tree.
Homework
Problem 5: Assuming negligible air resistance, what is the final speed of a rock thrown from a bridge?
Problem 6: How many DNA molecules can a single electron from an old-fashioned TV break?
A fundamental relationship that describes how the Universe works. These are the fundamental truths of Nature. When writing a principle as an equation, the "=" is translated as "causes." For example, Newton's 2nd Law, F = ma, a force F causes an object m to accelerate (change its speed or direction) a. These principles are where we begin our analyses.
The transfer of energy through microscopic collisions: fast moving (high-temperature) atoms colliding with slow moving (low-temperature) atoms results in the movement of energy from hot-to-cold.
Relevant to this course, the collisions could also be with photons.
The exchange of energy through the application of a force through some distance.
Particles of light. For a given frequency [latex] \nu [/latex], the smallest amount of energy that you can have is one photon's worth: [latex] E_\gamma = h \nu [/latex].
