Review from Chemistry of Application of Conservation of Energy to Photons and Atoms

Roger Hinrichs; Paul Peter Urone; Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; Richard Langley; Julianne Zedalis; John Eggebrecht; E.F. Redish

8 Review from Chemistry of Application of Conservation of Energy to Photons and Atoms

A Venn-diagram showing the different sciences

In your general chemistry courses, you already did some of what will be a big part of this unit: namely using the ideas of wave-particle duality in conjunction with conservation of energy. In chemistry, you did this in the context of looking at atomic transitions. In this chapter, you will review the ideas from chemistry, and then be exposed to some differences in how we will treat this same situation in a physics course. The reasons for the differences are three-fold. First, as described elsewhere in this book, each scientific discipline grew with its own history and conventions. The second reason for a different perspective is that the view taken by chemistry, while perfectly fine for all situations you encountered in that course, will break down for some of the situations we want to analyze in this course. The third, and arguably most important reason, mirrors the motivation for a variety of cultural perspectives in a humanities course: by exploring the same processes from different perspectives you gain a deeper and more holistic understanding of the material. Just as your understanding of history is incomplete if you only consider white men, so your understanding of conservation of energy is incomplete if you only look at it from a biology, chemistry, or physics perspective.

Review of Connecting Conservation of Energy to the Wave and Particle Natures of Light in the Context of the Hydrogen Atom from Chemistry^[1]

Instructor’s Notes

NOTE: This is review. If you are familiar with this material, feel free to skip to the problems at the end!

What we expect you to know from this review:

Electrons in atoms have discrete energy levels.
In order for an electron to transition from one level to another it must absorb or emit a photon with the exact amount of energy that corresponds to the energy difference. If the energy does not exactly match, then the transition will not occur.
If I know the energy difference, I can solve for the wavelength of the emitted photon.
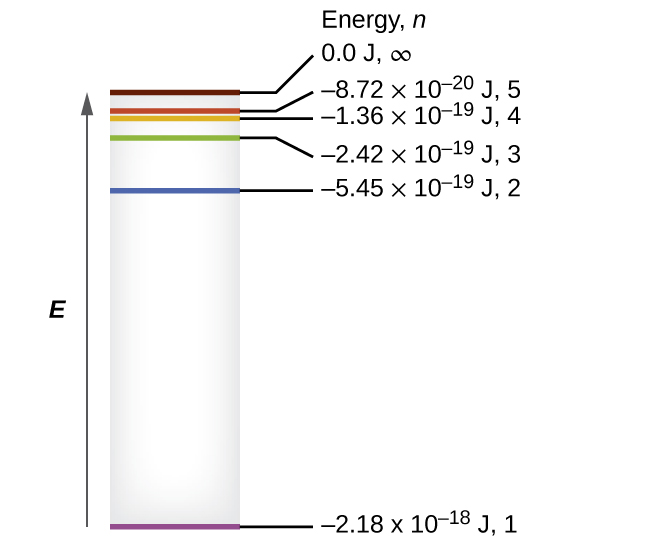
Be familiar with the idea of energy level diagrams such as the one shown below

A diagram showing the different electron energy levels as horizontal lines with vertical position representing energy.

The difference in energy levels in a hydrogen atom is

$\Delta E = - Rhc \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)$

where $R$ is the Rydberg constant $R = 1.097 \times 10^7 \, \mathrm{m}^{-1}$ .

Following the work of Ernest Rutherford and his colleagues in the early twentieth century, the picture of atoms consisting of tiny dense nuclei surrounded by lighter and even tinier electrons continually moving about the nucleus was well established. This picture was called the planetary model, since it pictured the atom as a miniature “solar system” with the electrons orbiting the nucleus like planets orbiting the sun. The simplest atom is hydrogen, consisting of a single proton as the nucleus about which a single electron moves. The electrostatic force attracting the electron to the proton depends only on the distance between the two particles. This classical mechanics description of the atom is incomplete, however, since as described in Basics of Light: Where does Light Come From? an electron moving in an orbit would be accelerating (by changing direction) and, according to classical electromagnetism, it should continuously emit electromagnetic radiation. This loss in orbital energy should result in the electron’s orbit getting continually smaller until it spirals into the nucleus, implying that atoms are inherently unstable.

In 1913, Niels Bohr attempted to resolve the atomic paradox by ignoring classical electromagnetism’s prediction that the orbiting electron in hydrogen would continuously emit light. Instead, he incorporated into the classical mechanics description of the atom Planck’s ideas of quantization and Einstein’s finding that light consists of photons whose energy is proportional to their frequency (Basics of Light: Introduction to the Photon). Bohr assumed that the electron orbiting the nucleus would not normally emit any radiation (the stationary state hypothesis), but it would emit or absorb a photon if it moved to a different orbit. The energy absorbed or emitted would reflect differences in the orbital energies according to this equation:

$\left| \Delta E \right| = \left| E_f - E_i \right| = \frac{hc}{\lambda}$

In this equation, h is Planck’s constant and E_i and E_f are the initial and final orbital energies, respectively. The absolute value of the energy difference is used, since frequencies and wavelengths are always positive. Instead of allowing for continuous values of energy, Bohr assumed the energies of these electron orbitals were quantized:

$E_n = -\frac{Rhc}{n^2}$

Where R is the so-called Rydberg constant that had been previously determined by experimental analysis of hydrogen spectra $R = 1.097 \times 10^7 \, \mathrm{m}^{-1}$ . Inserting this expression into the equation for $\Delta E$ gives

$\Delta E = -Rhc \left( \frac{1}{n_f}^2 - \frac{1}{n_i}^2 \right) = \frac{hc}{\lambda}$ .

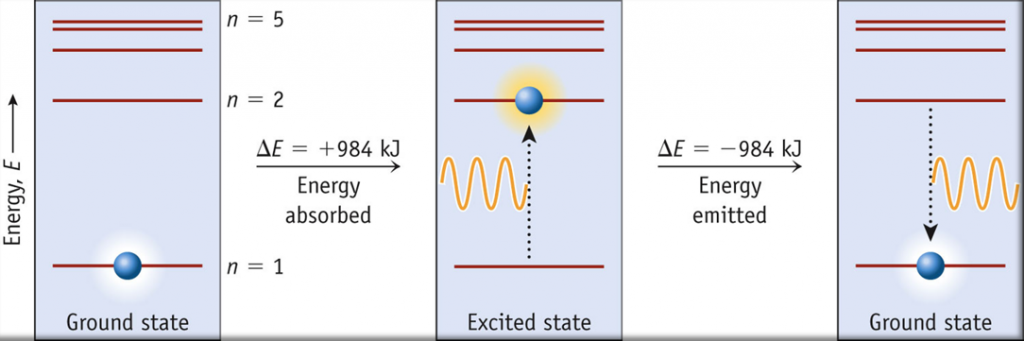
The lowest few energy levels are shown in Figure 1. One of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n = 1 orbit, the orbit in which it has the lowest energy. When the electron is in this lowest energy orbit, the atom is said to be in its ground electronic state (or simply ground state). If the atom receives energy from an outside source, it is possible for the electron to move to an orbit with a higher n value and the atom is now in an excited electronic state (or simply an excited state) with a higher energy. When an electron transitions from an excited state (higher energy orbit) to a less excited state, or ground state, the difference in energy is emitted as a photon. Similarly, if a photon is absorbed by an atom, the energy of the photon moves an electron from a lower energy orbit up to a more excited one. We can relate the energy of electrons in atoms to what we learned previously about energy. The law of conservation of energy says that we can neither create nor destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, that same amount of energy will be liberated when the electron returns to its initial state (Figure 2).

The energy levels of the hydrogen atom in the Bohr model — **Figure 1:** Quantum numbers and energy levels in a hydrogen atom. The more negative the calculated value, the lower the energy.

Calculating the Energy and Wavelength of Electron Transitions in Hydrogen Using Bohr’s Formula

What is the energy (in joules) and the wavelength (in meters) of the line in the spectrum of hydrogen that represents the movement of an electron from Bohr orbit with n = 6 to the orbit with n = 2? In what part of the electromagnetic spectrum do we find this radiation?

Solution

In this case, the electron starts out with n = 6, so n_i = 6. It comes to rest in the n = 2 orbit, so n_f = 2. The difference in energy between the two states is given by this expression:

$\Delta E = E_f - E_i = Rhc \left( \frac{1}{n_f} - \frac{1}{n_i} \right)$

$\Delta E = (1.097 \times 10^7 \, \mathrm{m}^{-1})(6.626 \times 10^{-34} \, \mathrm{J \cdot s})(3.00 \times 10^8 \, \mathrm{m/s}) \left( \frac{1}{2^2} - \frac{1}{6^2} \right)$

$\Delta E = -4.85 \times 10^{-19} \, \mathrm{J}$

This energy difference is negative, indicating a photon leaves the system (is emitted) as the electron falls from the n = 6 orbit to the n = 2 orbit.

The wavelength of a photon with this energy is found by the expression $E=hc/λ$ .

Rearrangement gives:

$\lambda = \frac{hc}{E}$

$\lambda = \frac{ (6.626\times 10^{-34} \, \mathrm{J \cdot s})(3.00 \times 10^8 \, \mathrm{m/s})}{4.85 \times 10^{-19} \, \mathrm{J}} = 4.10 \times 10^{-7} \, \mathrm{m}$

From the illustration of the electromagnetic spectrum in Basics of Light: The Main Parts of the Electromagnetic Spectrum, we can see that this wavelength is found in the violet portion of the electromagnetic spectrum.

Thinking about Atomic Transitions from a Physics Perspective

In chemistry, the starting point for the analysis was generally

$\Delta E = \frac{hc}{\lambda}$

or if, you were looking at the hydrogen atom specifically,

$\Delta E = - Rhc \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)$ .

Moreover, when solving the problem, you would probably just consider the absolute value of the change in energy and then figure out emission or absorption.

How would we look at this same problem in physics? In physics, we like to start with fundamental principles of the Universe and then apply definitions as described in Unit I On-A-Page: Principles and Definitions. In this case, the fundamental principle is Conservation of Energy: $\Delta E = Q + W$ ; this basic idea will, therefore be our starting point. To see how this works in practice, let’s look at an example, the $n = 6 \rightarrow n = 2$ transition discussed in the video.

The $n = 6 \rightarrow n = 2$ hydrogen transition from a physics perspective

Problem: What wavelength of light is does an electron in the $n = 6$ state of the hydrogen atom emit if it falls to the $n = 2$ state?

Solution – Starting with Principles:

First we identify the relevant fundamental principle of the Universe. In this situation, we know the relevant principle will be conservation of energy as the problem describes an electron losing energy as it moves from one state to another. Thus, we begin with

$\Delta E = Q + W$ .

Expanding out the $\Delta$ ,

$E_f - E_i = Q + W$ .

Now we need to consider the physics of the situation, or as I often call it, “what is the story that describes our phenomenon?” In this case, the story is:

I begin with an electron in a high energy state (n = 6). This electron then falls to a lower energy state (n=2). Since energy is conserved, that means that the energy lost by the electron has to go somewhere. In this case, the energy leaves the atom as light.

Having this story helps us fill in the parts of our conservation of energy equation:

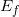$E_f$ : is the energy of the electron at the end. In our case, the energy of the n = 2 state: $E_{(n = 2)}$ .
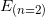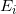$E_i$ : is the energy of the electron at the beginning. In our case, the energy of the n = 6 state: $E_{(n = 6)}$ .
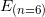Energy is leaving the atom through microscopic interactions, i.e. the emission of a photon. Thus, 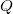$Q$ is the energy of the photon $E_\gamma$ .
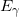There are no forces being applied to the atom. Since work is a force applied for some distance, 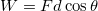$W = Fd \cos \theta$ , we know that the work in this case is zero: $W = 0$ .

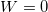Substituting our story into our equation ( $E_f \rightarrow E_{(n = 2)}$ , $E_i \rightarrow E_{(n = 6)}$ , $Q \rightarrow E_\gamma$ , and $W = 0$ ) then yields:

$E_{(n = 2)} - E_{(n = 6)} = E_\gamma + 0$ .

Now add definitions:

From what we have covered, thus far, we can now put in definitions for the various quantities:

We know, from reviewing chemistry in the section above, that the energy of an electron in the hydrogen atom is given by $E_n = \frac{-Rhc}{n^2}$ .

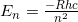We can now put these in definitions into our equation:

$\left( \frac{-Rhc}{2^2} \right) - \left( \frac{-Rhc}{6^2} \right) = E_\gamma$ .

Notice, as always, we are working in symbols which is one of our goals of the course. Now, we have a math problem! We are looking for $\lambda$ , which we can get from $E_\gamma$ , and $h$ , $c$ , and $R$ are all just constants of nature. We begin by noticing that we can factor out the $-Rhc$ on the left hand side:

$-Rhc \left( \frac{1}{2^2} - \frac{1}{6^2} \right) = \frac{1}{\lambda}$ .

(This should now be starting to look like what you reviewed from chemistry!) We, of course, know 2² and 6², converting these and substituting in the values for $R = 1.097 \times 10^7 \, \mathrm{m}^{-1}$ , $c = 3 \times 10^8 \, \mathrm{m/s}$ , and $h = 6.626 \times 10^{-34} \, \mathrm{J \cdot s}$ we have:

$\left( 1.097 \times 10^7 \, \mathrm{m}^{-1} \right)\left( 6.626 \times 10^{-34} \, \mathrm{J \cdot s} \right) \left( c = 3 \times 10^8 \, \mathrm{m/s} \right) \times \left( \frac{1}{4} - \frac{1}{36} \right) = E_\gamma$

$E_\gamma = -4.85 \times 10^{-19} \, \mathrm{J} = -3.02 \, \mathrm{eV}$

Notice, we never took any absolute values, and the result was negative. This negative sign has meaning! It tells us that the energy was lost to the atom! Of course, we already knew that, but this is a way to check our answers: we know energy is lost and we get a negative answer. The math takes care of itself!

Now we know from Basics of Light: Photon Momentum – Relationship to Energy that the energy of a photon is $E_\gamma = \frac{hc}{\lambda}$ , and can get a wavelength:

$E_\gamma = \frac{hc}{\lambda}$

Here we will take an absolute value, because negative wavelengths, unlike negative energies, don’t make sense. So we have

$\lambda = \frac{hc}{E_\gamma}$

$\lambda = \frac{ \left( 6.626 \times 10^{-34} \, \mathrm{J \cdot s} \right) \left( c = 3 \times 10^8 \, \mathrm{m/s} \right) }{ 4.85 \times 10^{-19} \, \mathrm{J} }$

$\lambda = 4.10 \times 10^{-7} \, \mathrm{m} = 410 \, \mathrm{nm}$

Exactly the blue line described in the video.

Why we do it this way

You may be saying to yourself, that the physics method seems a lot longer with a lot more steps. Why not just follow chemistry and start with

$\frac{hc}{\lambda} = -Rhc \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)$ ?

The reason for the physics approach is that it is a lot more versatile: it can be applied to loads of situations from x-ray emissions, to photo electric effects, to LEDs, to gravitational redshifts, to particle/anti-particle annihilations, to…, you get the idea. In contrast,

$\frac{hc}{\lambda} = -Rhc \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)$

works ONLY for the wavelengths of photons and ONLY for hydrogen atoms. Learning to think in the physics perspective is one of the goals for this course!

Homework Problem

Problem 25: Determine the wavelength of the third Balmer line (transition from n = 5 to n = 2 ).

Paul Flowers et al. Chemistry: Atoms First 2e. Open Stax, 2014. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Review of Connecting Conservation of Energy to the Wave and Particle Natures of Light in the Context of the Hydrogen Atom from Chemistry[1]

NOTE: This is review. If you are familiar with this material, feel free to skip to the problems at the end!

Thinking about Atomic Transitions from a Physics Perspective

Why we do it this way

License

Share This Book

Review of Connecting Conservation of Energy to the Wave and Particle Natures of Light in the Context of the Hydrogen Atom from Chemistry^[1]