5 Some Energy-Related Ideas that Might be New or are Particularly Important
Power
—the word conjures up many images: a professional football player muscling aside his opponent, a dragster roaring away from the starting line, a volcano blowing its lava into the atmosphere, or a rocket blasting off:

These images of power have in common the rapid performance of work, consistent with the scientific definition of power (P) as the rate at which work is done or energy is converted.
Power
Power is the rate at which work is done.
![]()
The SI unit for power is the watt (W), where 1 watt equals 1 joule/second (1 W=1 J/s).
Because work is energy transfer, power is also the rate at which energy is expended. A 60-W light bulb, for example, expends 60 J of energy per second. Great power means a large amount of work or energy developed in a short time. For example, when a powerful car accelerates rapidly, it does a large amount of work and consumes a large amount of fuel in a short time.
Calculating Power from Energy: Calculating the Power to Climb Stairs
What is the power output for a 60.0-kg woman who runs up a 3.00 m high flight of stairs in 3.50 s, starting from rest but having a final speed of 2.00 m/s? (See Figure 2.)
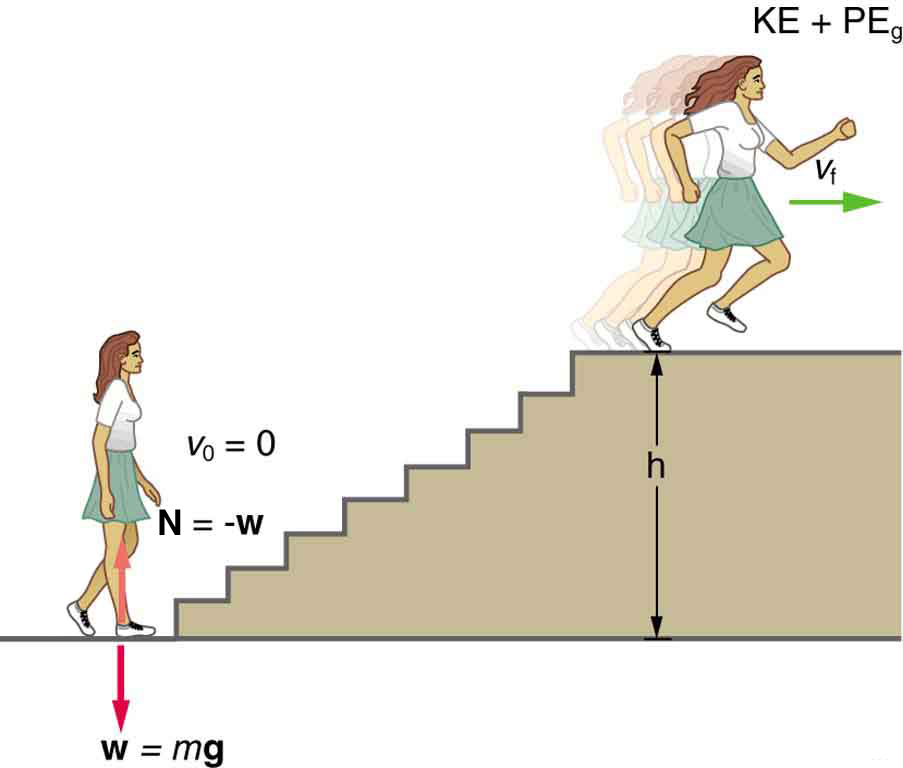
Strategy and Concept
The work going into mechanical energy is
![]()
There is no heat transfer in this situation, so ![]() .
.
![]()
![]()
![]()
At the bottom of the stairs, we take both ![]() and
and ![]() ; thus,
; thus,
![]()
![]()
where ![]() is the vertical height of the stairs and the minus sign means the energy is leaving her body.Because all terms are given, we can calculate work and then divide it by time to get power.
is the vertical height of the stairs and the minus sign means the energy is leaving her body.Because all terms are given, we can calculate work and then divide it by time to get power.
Solution
Substituting the expression for W in the previous equation, ![]() yields
yields
![]()
![]()
Entering known values yields
![]()
Discussion
The woman does 1764 J of work to move up the stairs compared with only 120 J to increase her kinetic energy; thus, most of her power output is required for climbing rather than accelerating.
It is impressive that this woman’s useful power output is slightly less than 1 horsepower (1 hp=746 W)! People can generate more than a horsepower with their leg muscles for short periods of time by rapidly converting available blood sugar and oxygen into work output. (A horse can put out 1 hp for hours on end.) Once oxygen is depleted, power output decreases and the person begins to breathe rapidly to obtain oxygen to metabolize more food—this is known as the aerobic stage of exercise. If the woman climbed the stairs slowly, then her power output would be much less, although the amount of work done would be the same.
Making Connections: Take-Home Investigation—Measure Your Power Rating
Determine your own power rating by measuring the time it takes you to climb a flight of stairs. We will ignore the gain in kinetic energy, as the above example showed that it was a small portion of the energy gain. Don’t expect that your output will be more than about 0.5 hp.
Examples of Power
Examples of power are limited only by the imagination, because there are as many types as there are forms of work and energy. (See Table 1 for some examples.) Sunlight reaching Earth’s surface carries a maximum power of about 1.3 kilowatts per square meter (kW/m2). This quantity of power per area is called , and will be explored more in the chapter on Basics of Waves.
A tiny fraction of this is retained by Earth over the long term. Our consumption rate of fossil fuels is far greater than the rate at which they are stored, so it is inevitable that they will be depleted. Power implies that energy is transferred, perhaps changing form. It is never possible to change one form completely into another without losing some of it as thermal energy. For example, a 60-W incandescent bulb converts only 5 W of electrical power to light, with 55 W dissipating into thermal energy. Furthermore, the typical electric power plant converts only 35 to 40% of its fuel into electricity. The remainder becomes a huge amount of thermal energy that must be dispersed as heat transfer, as rapidly as it is created. A coal-fired power plant may produce 1000 megawatts; 1 megawatt (MW) is 106 W of electric power. But the power plant consumes chemical energy at a rate of about 2500 MW, creating heat transfer to the surroundings at a rate of 1500 MW. (See Figure 3.)

| Table 1: Power Output or Consumption | |
| Object or Phenomenon | Power in Watts |
| Milky Way galaxy | 1037 |
| The Sun | 4×1026 |
| Volcanic eruption (maximum) | 4×1015 |
| Lightning bolt | 2×1012 |
| Nuclear power plant (total electric and heat transfer) | 3×109 |
| Aircraft carrier (total useful and heat transfer) | 108 |
| Dragster (total useful and heat transfer) | 2×106 |
| Car (total useful and heat transfer) | 8×104 |
| Football player (total useful and heat transfer) | 5×103 |
| Clothes dryer | 4×103 |
| Person at rest (all heat transfer) | 100 |
| Typical incandescent light bulb (total useful and heat transfer) | 60 |
| Heart, person at rest (total useful and heat transfer) | 8 |
| Electric clock | 33 size 12{3} {} |
| Pocket calculator | 10−3 |
Power and Energy Consumption
We usually have to pay for the energy we use. It is interesting and easy to estimate the cost of energy for an electrical appliance if its power consumption rate and time used are known. The higher the power consumption rate and the longer the appliance is used, the greater the cost of that appliance. The power consumption rate is ![]() , where
, where ![]() is the energy supplied by the electricity company. So the energy consumed over a time
is the energy supplied by the electricity company. So the energy consumed over a time ![]() is
is
![]()
Electricity bills state the energy used in units of kilowatt-hours (kW⋅h) which is the product of power in kilowatts and time in hours. This unit is convenient because electrical power consumption at the kilowatt level for hours at a time is typical.
Calculating Energy Costs
What is the cost of running a 0.200-kW computer 6.00 h per day for 30 days if the cost of electricity is $0.120 per kW⋅hkW⋅h?
Strategy
Cost is based on energy consumed; thus, we must find ![]() and then calculate the cost. Because electrical energy is expressed in kW⋅h, at the start of a problem such as this it is convenient to convert the units into kW and hours.
and then calculate the cost. Because electrical energy is expressed in kW⋅h, at the start of a problem such as this it is convenient to convert the units into kW and hours.
Solution
The energy consumed in kW⋅h is
![]()
![]()
![]()
and the cost is simply given by
cost=(36.0 kW⋅h)($0.120 per kW⋅h)=$4.32 per month
Discussion
The cost of using the computer in this example is neither exorbitant nor negligible. It is clear that the cost is a combination of power and time. When both are high, such as for an air conditioner in the summer, the cost is high.
The motivation to save energy has become more compelling with its ever-increasing price. Armed with the knowledge that energy consumed is the product of power and time, you can estimate costs for yourself and make the necessary value judgments about where to save energy. Either power or time must be reduced. It is most cost-effective to limit the use of high-power devices that normally operate for long periods of time, such as water heaters and air conditioners. This would not include relatively high power devices like toasters, because they are on only a few minutes per day. It would also not include electric clocks, in spite of their 24-hour-per-day usage, because they are very low power devices. It is sometimes possible to use devices that have greater efficiencies—that is, devices that consume less power to accomplish the same task. One example is the compact fluorescent light bulb, which produces over four times more light per watt of power consumed than its incandescent cousin.
Modern civilization depends on energy, but current levels of energy consumption and production are not sustainable. The likelihood of a link between global warming and fossil fuel use (with its concomitant production of carbon dioxide), has made reduction in energy use as well as a shift to non-fossil fuels of the utmost importance. Even though energy in an isolated system is a conserved quantity, the final result of most energy transformations is waste heat transfer to the environment, which is no longer useful for doing work.
Problem 7: How long can you play tennis off a candy bar?
Problem 8: How long for a car of fixed power to get up to speed?
Units of Energy

Instructor’s Notes
- Converting between the different units of energy
In this course, we will be using Joules, electron-Volts exclusively, and kW-hrs exclusively. We are including these other units for your reference.
Note that the eV is significantly smaller than the joule; eV will generally be the smallest unit of energy used in this course.
If energy is defined as the ability to do work, then energy and work must have the same units. Thus, the SI unit of the energy is the Joule (recall 1J=1Nm=1kgms2). Energy, however, is one quantity where there are many other units in common use in scientific literature including electron-Volts (eV), kilowatt-hours (kW∙hr), calories, and Calories.
Electron-Volts
A common quantity in chemistry is the electron-Volt or eV. One electron-Volt is the amount of energy gained by an electron as it travels between the two ends of a 1 Volt battery (a concept that will be discussed in more detail when you study electricity). Numerically, 1eV = 1.602×10-19J. The reason this unit is common in chemistry is that the energies of atomic bonds are typically about 1eV as shown in the table below. The bond-dissociation energy is the energy released when the bond is formed.
| Bond | Bond-dissociation energy at 298K (eV/Bond) | Comment |
| C-C | 3.60-3.69 | Strong, but weaker than C–H bonds |
| Cl-Cl | 2.51 | Indicated by the yellowish colour of this gas |
| H-H | 4.52 | Strong, nonpolarizable bondCleaved only by metals and by strong oxidants |
| O-H | 4.77 | Slightly stronger than C–H bonds |
| OH-H | 2.78 | Far weaker than C–H bonds |
| C-O | 11.16 | Far stronger than C–H bonds |
| O-CO | 5.51 | Slightly stronger than C–H bonds |
| O=O | 5.15 | Stronger than single bondsWeaker than many other double bonds |
| N=N | 9.79 | One of the strongest bondsLarge activation energy in production of ammonia |
| H3C-H | 4.550 | One of the strongest aliphatic C–H bonds |
Kilowatt Hours and Calories
Ad described above, when you buy electricity from the power company, the bill says how many kilowatt hours you have purchased. A Watt is a unit of a quantity called and 1 Watt is equal to 1 Joule/second: 1W = 1 J/s. Thus, a kilowatt hour is therefore:
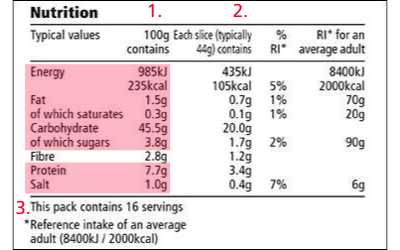
The calorie is an imperial unit of energy that is still in common use in the nutritional sciences in the United States. One calorie (lowercase c) is the amount of energy needed to raise 1g of water 1oC or 1 cal = 4.814J. On food labels, you will see energy listed in Calories (capital C). One Calorie is equal to 1kilocalorie; in other words, 1 Cal = 1000 cal. Thus, one 1 Cal = 4814 J. In other countries, you will see food labels in both Calories and Joules like the one shown below.
The Potential Energy of Electrons in Atoms and Molecules
For this first unit, the primary source of microscopic potential energy with which we shall concern ourselves is the potential energy stored be electrons in atoms and in chemical bonds: ![]() . This potential energy is a result of the force of electrical attraction between different atoms (recall electricity and magnetism was one of our fundamental forces) or between an electron and its nucleus.
. This potential energy is a result of the force of electrical attraction between different atoms (recall electricity and magnetism was one of our fundamental forces) or between an electron and its nucleus.
The strength of chemical bonds is typically quoted in one of two ways: either the energy in the bond, called the bond dissociation energy, is quoted directly (typically in eV) or the enthalpy per mole will be quoted. For example, the Cl-Cl bond has a bond dissociation energy of 2.51 eV/bond or a bond dissociation enthalpy per mole of ΔH=242kJ/mol. For atoms, the relevant energy is the ionization energy, which is the amount of energy needed to remove an electron: quoted directly in eV or, occasionally in kJ/mol. How do we interpret these numbers in terms of potential energy? We use the same freedom to choose the zero of potential energy discussed in Unit IV – Chapter 3.3: Macroscopic Potential Energy from the Physics 131 textbook which discusses potential energy at the macroscopic scale.
Thinking about gravity, we tend to put the zero of potential energy at ground level; objects above the ground then have positive potential energy while objects underground have negative potential energy. This use of negative potential energy makes sense, an object at ground level will fall to below ground level if allowed to do so and lose energy in the process.

 Where to put the zero of gravitational potential energy? The top of a building? The ground? In the subway below? The choice is arbitrary.
Where to put the zero of gravitational potential energy? The top of a building? The ground? In the subway below? The choice is arbitrary.For atoms and molecules, we have a similar freedom to choose where to put zero potential energy. The standard convention is to say that free atoms that are far apart have zero potential energy. Atoms in most bonds have lower potential energy than free atoms (that is why the bonds form!). Therefore the potential energy of the atoms is less than zero: the potential energy of atoms in bonds is negative. This may seem like a weird choice for the zero of potential energy, but it is the convention and it makes sense when you think about it!
Let’s return to the quoted Cl-Cl bond with dissociation energy of 2.51 eV/bond. What does this value mean? It means that two Cl atoms bonded together have a potential energy of 2.51 eV less than if they were free. Said another way, the potential energy of Cl atoms in Cl2 is -2.51 eV, while the potential energy of free Cl atoms is 0 eV. This is consistent with what you probably already know about Chlorine: Cl2 is the lower energy state than free Cl atoms. I would get 2.51 eV of energy for every Cl-Cl bond that is formed, as the atoms move from zero potential energy to -2.51 eV. Similarly, I would need to add 2.51 eV of energy to break a Cl-Cl bond and move the two atoms up to zero potential energy. The same idea holds for electrons in atoms. If you look up the ionization energy of hydrogen, you will see 13.6 eV. This value meas that the electron has 13.6 eV lesspotential energy than if it were free. Thus, a more accurate way to write this energy would be U = -13.6 eV.
The Connection Between Kinetic Energy and Momentum
We will now develop a useful relationship between momentum and kinetic energy. This is a useful relationship that we will use throughout this course.
By now you should have refreshed your memory and know that for a standard particle with mass, such as an electron, the momentum of the particle is
![]()
and the kinetic energy of the particle is
![]() .
.
If you look at these two expressions, they are fairly similar, both involve the mass of the particle ![]() and its velocity
and its velocity ![]() .
.
Now there are some important differences. The momentum is a vector, including the direction of motion, whereas the kinetic energy is a scalar and is independent of the particle’s direction of motion. However, there’s a useful way to relate these two.
Begin with the magnitude of the momentum, removing the vectors, in which case is just
![]() .
.
Square both sides of this expression so you have
![]() .
.
Now divide both sides of the expression by ![]() , so now you have
, so now you have
![]() ,
,
Which is the kinetic energy.
The big punch line is that the kinetic energy of a particle with mass is
![]() .
.
This is a useful expression that we’ll be using throughout this course.
The energy or work per time. The unit is the J/s or the Watt (W)
Power per area:
I = P/A
or, using P = E/t,
I = E/(At)

