Basics of Light

Roger Hinrichs; Paul Peter Urone; Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; Richard Langley; Julianne Zedalis; John Eggebrecht; E.F. Redish

7 Basics of Light

Where Does Light Come From?

Light is generated any time a charge undergoes acceleration; this is a connection to an idea from Physics 131. Just like in Physics 131 it’s not the motion of the charge that matters, but its acceleration. Moving charges don’t generate light only accelerating ones do. To expand upon this connection to 131 a little bit more, if a charge accelerates by slowing down, it is still accelerating then from Newton’s second law,

$\sum \vec{F} = m \vec{a}$

, we know that a force has acted upon it. If it takes some distance for this slowing down to occur, then the force must have been applied for some distance and we know that work was therefore done on the charged particle. By the statement of conservation of energy, or equivalently the first law of thermodynamics, if work is done on a particle then the particles energy must change, that energy must go somewhere and where does it often go? It goes into light.

Here’s an example with which you might be familiar from your chemistry class. An electron in an outer energy level of an atom falls to a lower energy level. There’s a change in energy as the electron falls, that energy has to go somewhere. It goes into the release of light.

Electrons changing energy levels, however, is not the only way to produce light. Think about an old-school incandescent lamp with the filament in it that get hot as you turn them on, to understand why these incandescent lights give off light we have to understand a little bit about what temperature is.

Recall from Physics 131 that temperature is related to the average kinetic energies of particles moving around randomly on the atomic and subatomic scales. As these particles are bouncing around randomly, they’re changing directions. From 131 we know that acceleration is a vector, so because velocity changes direction, then we know that there is acceleration. So once again, even any object with temperature will emit light due to the accelerating charges bouncing around on the atomic and subatomic scale.

Instructor’s Notes

In summary

Light is generated by charges accelerating.
Every object with a temperature (i.e. everything) will emit some amount of light of some type.
Our eyes, however, are only sensitive to certain kinds of light and we therefore cannot see this light from everyday objects such as you and I. We don’t see light coming off of us because our eyes are not sensitive to the kind of light that we emit due to our temperature.
However, we can build devices that can see the light given off by more everyday objects such as people by using technologies such as infrared cameras.

Homework

Problem 17: Which situations will create electromagnetic radiation?

Properties of Light

Instructor’s Notes

The video for this section uses $f$ for frequency. The text, on the other hand uses $\nu$ . This is a good example of the fact that you need to get used to the idea that different disciplines use different letters for the same quantity!

On your equation sheet, in class, an on exams, we will use $\nu$ to be consistent with what you have used in chemistry.

Like all waves, light waves are characterized by a , a , a speed, which follows the usual relationship of $v = \lambda \nu$ , and an . However, there are some important unique characteristics of light waves. For light, the wave in the vacuum speed is always the same, $c = 3 \times 10^8 \, \mathrm{m}/\mathrm{s}$ . In a vacuum $v = \lambda \nu$ , turns into $c = \lambda \nu$ , because all light waves, regardless of their wavelength or frequency or amplitude, travel at this same fundamental speed.

For the amplitude of the light wave we will not use the symbol $A$ we will instead use the symbol $E$ and the amplitude of a light wave has the units of Newton’s per Coulomb $\mathrm{N}/\mathrm{C}$ , Newton’s are the unit of force and Coulomb, as you’ve already discussed elsewhere in your prep, is the unit of a charge. The amplitude of a light wave is a Newton per Coulomb. We will see why this is the unit of a light waves amplitude later in this particular course, but for right now you just need to know that those are the units.

There are many different kinds of light. Where do these different kinds of light come from? Well different wavelengths or frequencies represent different kinds of light. Light is also sometimes called electromagnetic radiation, and so the kinds of light are called the E/M spectrum. You’ll see the terms ‘electromagnetic spectrum’ or ‘E/M spectrum’ used, which just means the kinds of light. You’ll explore more of the different kinds of light in the next section.

But this is giving you a bit of a hint on where this whole course is going and how light, electricity, and magnetism are all going to be deeply connected in some fundamental way, which will come to by the end of this course.

We’ve now seen that the frequency or wavelength of a light wave tells us what kind of light we are going to have. What does the amplitude of the light wave correspond to?

The amplitude, remember we’re using $E$ for the amplitude, is related to the intensity of the light, as in the watts per square meter, by this expression

$I = \frac{1}{2} c \epsilon_0 E^2$

where $c$ is the usual speed of light $c = 3 \times 10^8 \, \mathrm{m}/\mathrm{s}$ and $\epsilon_0$ is a property of just empty space. You might not think of empty space as having properties, but it does! The quantity $\epsilon_0$ is a property of empty space called the permittivity of free space, and it has this value $\epsilon_0 = 8.85 \times 10^{-12} \, \frac{\mathrm{C}^2}{\mathrm{J} \cdot \mathrm{m}}$ . We will talk more about this number throughout this course, for now, you just need to know it’s a property of empty space.

An example converting between wavelength and frequency for light (from Chemistry – so this should be familiar!)

Let’s do some examples what is what is the frequency of light that has 396.15 nanometer as wavelength?

Solution:

Wavelength equals c over frequency: $\lambda = c / \nu$ , meaning that frequency equals c over lambda $\nu = c / \lambda$ . The speed of light in vacuum is given: $2.998 \times 10^8 \, \mathrm{m/s}$ . For this question, the wavelength is in nanometers while the unit of the speed of light is in meters, so I know that I have to change the nanometer:

$\nu = \frac{c}{\lambda}$

$\nu = \frac{2.998 \times 10^8 \, \mathrm{m/s}}{\left( 396.15 \, \mathrm{nm} \right) \left(\frac{10^{-9} \, \mathrm{m}}{\mathrm{nm}} \right)}$

$\nu = 7.568 \times 10^{14} \, \mathrm{s}^{-1} = 7.568 \times 10^{14} \, \mathrm{Hz}$

Discussion:

That means $7.568 \times 10^{14}$ is how many waves will pass per one second.

Instructor’s Notes

In summary

Light is a wave with a: wavelength, frequency, speed, and amplitude.
The speed of all light waves in vacuum is the same $c = 3 \times 10^8 \, \mathrm{m}/\mathrm{s}$
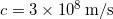
The units of the amplitude of a light wave are Newtons/Coulomb
We will use 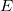for the amplitude of a light wave instead of .
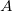- Keep in mind this is NOT the energy!
- The amplitude has units Newtons/Coulomb
- Newtons/Coulomb are not the same unit as the Joules we use for energy!
- I know it is confusing, but we are running out of letters and there is a good reason for 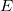$E$ which we will see later in the course
While, in general, we know that intensity is proportional to amplitude squared 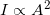$I \propto A^2$ , for light we have exact equation:

$I = \frac{1}{2} c \epsilon_0 E^2$

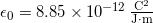$\epsilon_0 = 8.85 \times 10^{-12} \, \frac{\mathrm{C}^2}{\mathrm{J} \cdot \mathrm{m}}$ is a constant of the Universe, just like the speed of light. We will revisit this constant later.

Homework Problem

Problem 18: Speed dependencies for electromagnetic waves.

Problem 19: What is the frequency of a radio station given the wavelength?

The Main Parts of the Electromagnetic Spectrum

Instructor’s Notes

As scientifically trained people, you should have a basic familiarity with the electromagnetic spectrum. Thus, while this course is generally not about memorization, I will ask you to memorize the large basic divisions of the electromagnetic spectrum: radio, microwaves, infrared, visible, ultraviolet, x-rays, and gamma rays. You need to know that radio represents the longest wavelength and gamma rays represent the shortest wavelength. You should also know that, within visible light, red is the longest going through the rainbow to violet. You do NOT need to know the frequencies or wavelengths corresponding to each range. The only exception to this rule is that I do expect you to know that red is about 700nm wavelength while violet is about 350nm. The different types of radiation come up so frequently in scientific discussion that it is important to know some basic facts.

A Venn-diagram showing the different sciences

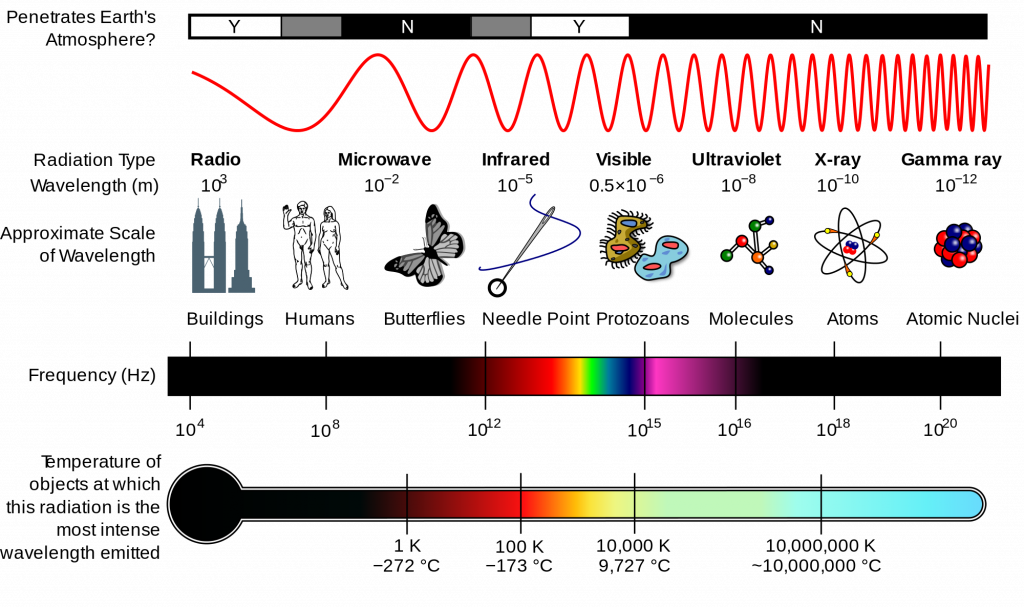
Below, you can find a video that summarizes the parts of the electromagnetic spectrum taken from General Chemistry I (Chem 111 at UMass-Amherst), prepared by Dr. Al-Hariri. Please use it to familiarize yourself with the parts of the spectrum if needed.

An additional graphic can be found below the video and its transcript.

Everyday we’re bombarded with different types of radiation like the radio radiation from radio tower close to us, to microwave radiation, to the light radiation and so on; and if you look at the different wavelengths displayed in this picture you can see that the difference between between them is the length of that wave

Now, here are a couple of different types of electromagnetic radiation and the difference way and the different wavelengths of each:

the infrared radiation with the wavelengths in the range of 10^-5 meter, which is relatively the same size as pen tip.
The microwave radiation with wavelengths of about 10^-3 m, which is in the range of a dice.
The radio the radio wave, which is the FM and AM: the wavelengths is in the range of 10³ m, in the range of a mountain.
The gamma radiationm which is harmful radiation for us, 10^-12 m, about the atomic nucleus.
The X-ray 10^-10 m.
The ultraviolet in the range of the DNA size and that would be 10^-6 m.
And lastly the visible light which is the light that we can see with our own eyes is in the range of 10^-6 m and the same size as a bacteria.

Different electromagnetic radiations have different wavelengths.

A diagram of the Milton spectrum, showing the type, wavelength (with examples), frequency, the black body emission temperature. — **Figure 1:** A diagram of the EM spectrum, showing the type, wavelength (with examples), frequency, the black body emission temperature. (Inductiveload, NASA [CC BY-SA (http://creativecommons.org/licenses/by-sa/3.0/)])

Homework Problem

Problem 20: Rank the types of waves in the EM spectrum by wavelength.

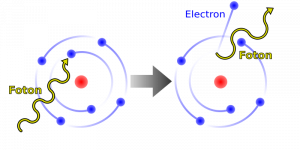
Introduction to the Photon

We’ve talked about light as a wave, we’ve talked about its frequency, its wavelength, its speed, its amplitude. We’ve talked about the wave properties of light, now we’re going to move and think about the particle properties of light. What happens when we think of light as a particle as opposed to as a wave?

Let’s say we have a laser, can I keep making this laser dot dimmer and dimmer and dimmer forever? This may seem like a very abstract philosophical question. I’m going to flip it on its head for you. Can I take a sample of water and keep reducing its amount forever? No, eventually I get down to one water molecule, and I’m done. This was the basis for the atomic theory. You can’t separate matter forever. I’m just asking you the exact same question for a dot of light, can I keep having it forever? And it turns out the answer is no, I can’t. At some point I reach the bottom, there’s a smallest dimness, just like there’s a smallest amount of water you can have, there’s a smallest amount of light you can have, and we call this smallest amount of light we say it’s a particle of light, and we call it a photon, and we are going to use this symbol $\gamma$ , the Greek letter gamma, for photon.

We can think of this laser as a light wave, where I change the amplitude to make it brighter or darker, or we can flip that on its head and say it’s a bunch of photons flying along together and to make it brighter or darker I changed the number of photons. Already we’re sort of bouncing back and forth between thinking of things as waves and particles. This photon image is really good when we think about light being absorbed by materials or emitted from materials; that’s when thinking in terms of particles tends to be a good picture. Waves on the other hand tend to do really well when we’re thinking about light flying through space.

Let’s go through the properties of the photon. We are now imagining light to be made up of little balls, but we are imagining them to be made up of little massless spheres. Little massless particles that travel at the speed of light, $c$ . But even though they are massless they still carry energy and momentum.

Thinking about detecting/absorbing light? Think particles!

Almost all detection systems talked about thus far—eyes, photographic plates, photomultiplier tubes in microscopes, and CCD cameras—rely on particle-like properties of photons interacting with a sensitive area. A change is caused and either the change is cascaded or zillions of points are recorded to form an image we detect. These detectors are used in biomedical imaging systems, and there is ongoing research into improving the efficiency of receiving photons, particularly by cooling detection systems and reducing thermal effects.

Photon Momentum – Relationship to Wavelength

In this part, we are explicitly trying to delve deeper into an equation you saw in Chemistry: $E = \frac{hc}{\lambda}$ . We will see that this equation, while fine for chemistry, is NOT a fundamental principle and thus will NOT be a starting point for us in this class. If you wish to review the chemistry perspective, watch the video below. The video has captions. I did not include the transcript as this video is simply provided to review the chemistry perspective, not as a main focus for our course.

The quantum of EM radiation we call a photon has properties analogous to those of particles we can see, such as grains of sand. A photon interacts as a unit in collisions or when absorbed, rather than as an extensive wave. Massive quanta, like electrons, also act like macroscopic particles—something we expect, because they are the smallest units of matter. Particles carry momentum as well as energy. Despite photons having no mass, there has long been evidence that EM radiation carries momentum. (Maxwell and others who studied EM waves predicted that they would carry momentum.) It is now a well-established fact that photons do have momentum. In fact, photon momentum is suggested by the photoelectric effect, where photons knock electrons out of a substance. Figure 2 shows macroscopic evidence of photon momentum.

(a) Trajectory of a comet with a nucleus and tail as it passes by the Sun is shown as a partial parabolic path with Sun near the vertex of the parabolic path. (b) The photograph of a moving Hale Bopp comet in space is shown as bright lighted object. — **Figure 2:** The tails of the Hale-Bopp comet point away from the Sun, evidence that light has momentum. Dust emanating from the body of the comet forms this tail. Particles of dust are pushed away from the Sun by light reflecting from them. The blue ionized gas tail is also produced by photons interacting with atoms in the comet material. (credit: Geoff Chester, U.S. Navy, via Wikimedia Commons).

Figure 2. shows a comet with two prominent tails. What most people do not know about the tails is that they always point away from the Sun rather than trailing behind the comet (like the tail of Bo Peep’s sheep). Comet tails are composed of gases and dust evaporated from the body of the comet and ionized gas. The dust particles recoil away from the Sun when photons scatter from them. Evidently, photons carry momentum in the direction of their motion (away from the Sun), and some of this momentum is transferred to dust particles in collisions. Gas atoms and molecules in the blue tail are most affected by other particles of radiation, such as protons and electrons emanating from the Sun, rather than by the momentum of photons.

Conservation of Momentum

Not only is momentum conserved in all realms of physics, but all types of particles are found to have momentum. We expect particles with mass to have momentum, but now we see that massless particles including photons also carry momentum.

Some of the earliest direct experimental evidence of photon momentum came from scattering of X-ray photons by electrons in substances, named Compton scattering after the American physicist Arthur H. Compton (1892–1962). Around 1923, Compton observed that X-rays scattered from materials had a decreased energy and correctly analyzed this as being due to the scattering of photons from electrons. This phenomenon could be handled as a collision between two particles—a photon and an electron at rest in the material. Energy and momentum are conserved in the collision. (See Figure) He won a Nobel Prize in 1929 for the discovery of this scattering, now called the Compton effect, because it helped prove that photon momentum is given by the de Broglie relation

$p = \frac{h}{\lambda}$

where $h$ is Planck’s constant: a fundamental constant of the Universe (just like the speed of light $c$ or $\epsilon_0$ ). The value for Planck’s constant is $h = 6.626 \times 10^{-34} \, \mathrm{J \cdot s}$ , or in terms of electron volts eV (described in the review of energy) $h = 4.135 \times 10^{-15} \, \mathrm{eV \cdot s}$ . This constant, like all constants, is provided on your equation sheet.

Instructor’s Note

We will see in a later chapter on matter waves, that this same relation works for electrons as well. Thus, the de Broglie relation

$p = \frac{h}{\lambda}$

is one of the fundamental principles for this unit! It connects the particle nature of matter ( $p$ is a particle property) and matter’s wave nature ( $\lambda$ is a wave property).

The Compton effect is the name given to the scattering of a photon by an electron shown in Figure 3. Energy and momentum are conserved, resulting in a reduction of both for the scattered photon. Studying this effect, Compton verified that photons have momentum. We can see that photon momentum is small, since p=h/λ, and h is very small. It is for this reason that we do not ordinarily observe photon momentum. Our mirrors do not recoil when light reflects from them (except perhaps in cartoons). Compton saw the effects of photon momentum because he was observing x rays, which have a small wavelength and a relatively large momentum, interacting with the lightest of particles, the electron. We will explore this particular phenomenon more in class.

Collision of an electron with a photon of energy E equal to h f is shown. The electron is represented as a spherical ball and the photon as an ellipse enclosing a wave. After collision the energy of the photon becomes E prime equal to h f prime and the final energy of an electron K E sub e is equal to E minus E prime. The direction of electron and photon before and after collision is represented by arrows. — **Figure 3:** The Compton effect is the name given to the scattering of a photon by an electron. Energy and momentum are conserved, resulting in a reduction of both for the scattered photon. Studying this effect, Compton verified that photons have momentum.

Electron and Photon Momentum Compared

(a) Calculate the momentum of a visible photon that has a wavelength of 500 nm. (b) Find the velocity of an electron having the same momentum.

Strategy

Finding the photon momentum is a straightforward application of its definition: $p = h/\lambda$ . Then, we use the formulas we know from 131 to find the electron’s momentum and velocity.

Solution for (a)

Photon momentum is given by the equation:

$p = h/\lambda$ .

Entering the given photon wavelength yields

$p = \frac{6.63 \times 10^{-34} \, \mathrm{J \cdot s}}{500 \times 10^{-9} \, \mathrm{m}} = 1.33 \times 10^{-27} \, \mathrm{kg \cdot m/s}$ .

Solution for (b)

Since this momentum is indeed small, we will use the classical expression $p=mv$ to find the velocity of an electron with this momentum. Solving for v and using the known value for the mass of an electron gives

$v = \frac{p}{m} = \frac{1.33 \times 10^{-27} \, \mathrm{kg \cdot m/s}}{9.11 \times 10^{-31} \, \mathrm{kg}} = 1460 \, \mathrm{m/s}$ .

Discussion

Photon momentum is indeed small. Even if we have huge numbers of them, the total momentum they carry is small. An electron with the same momentum has a 1460 m/s velocity, which is clearly nonrelativistic. A more massive particle with the same momentum would have an even smaller velocity. This is borne out by the fact that it takes far less energy to give an electron the same momentum as a photon. But on a quantum-mechanical scale, especially for high-energy photons interacting with small masses, photon momentum is significant. Even on a large scale, photon momentum can have an effect if there are enough of them and if there is nothing to prevent the slow recoil of matter. Comet tails are one example, but there are also proposals to build space sails that use huge low-mass mirrors (made of aluminized Mylar) to reflect sunlight. In the vacuum of space, the mirrors would gradually recoil and could actually take spacecraft from place to place in the solar system. (See Figure 4.)

(a) A payload having an umbrella-shaped solar sail attached to it is shown. The direction of movement of payload and direction of incident photons are shown using arrows. (b) A photograph of the top view of a silvery space sail. — **Figure 4:** (a) Space sails have been proposed that use the momentum of sunlight reflecting from gigantic low-mass sails to propel spacecraft about the solar system. A Russian test model of this (the Cosmos 1) was launched in 2005, but did not make it into orbit due to a rocket failure. (b) A U.S. version of this, labeled LightSail-1, is scheduled for trial launches in the first part of this decade. It will have a 40-m2 sail. (credit: Kim Newton/NASA)

Homework Problems

Problem 21: Find the momentum of a microwave photon.

Photon Momentum – Relationship to Energy

Photons, in addition to having energy, also have momentum. This is the part that tends to get folks, because in 131. we told you that momentum was mass times velocity which is mostly true. It’s true as long as you’re not going too fast, once you start getting close to the speed of light this will actually break down on you. You need a new expression. But as long as you’re going slow, this is fine. But clearly this does not work for photons because for photons mass is zero. Special relativity has an answer, it’s the momentum of a photon is the energy divided by the speed of light,

$p=\frac{E_\gamma}{c}$ or $E_\gamma = pc$ .

Instructor’s Note

If you look at the Unit I On-a-Page, you will see that this is one of the fundamental definitions of this unit: the definition of a photon’s momentum in terms of its energy

$p=\frac{E_\gamma}{c}$ .

A way to help keep all of these formula straight: if the formula contains a $c$ then it only applies to light, if the formula contains an $m$ , then it only applies to particles with mass (like electrons)!

From the fundamental principle of this unit, the de Broglie relation $p = \frac{h}{\lambda}$ , and this definition of a photon’s momentum in terms of its energy $p=\frac{E}{c}$ , we can derive a formula that was given to you in your chemistry classes. While I, in general, try to avoid derivations, I think this one is useful as it is short and shows you why what you learned in chemistry is the way it is. That is, after all, one of the motivations for this unit: why does chemistry work?

So we know, $p = \frac{h}{\lambda}$ and $p=\frac{E}{c}$ . Since both equations are equal to $p$ , we can set them equal to each other:

$\frac{h}{\lambda} = \frac{E_\gamma}{c}$

which, after some rearranging (move the $c$ over) we get the familiar

$E = \frac{hc}{\lambda}$ .

You can start with this equation that you know from chemistry. However, keep in mind that it is NOT a fundamental relationship: it comes from combining:

The fundamental principle of the de Broglie relation: 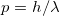$p = h/\lambda$ that connects the wave and particle natures for all matter.
The definition of a photon’s momentum in terms of its energy: 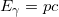$E_\gamma = pc$ , which is only specific to photons.

Therefore, the relationship $E = \frac{hc}{\lambda}$ only applies to photons. I have seen many students make mistakes of trying to apply it to electrons!

Compare the Energies of the Photon and Electron from the Last Example

What is the energy of the 500 nm photon, and how does it compare with the energy of the electron with the same momentum?

The electron:

There are two ways of approaching this problem.

1. Use the fact that we know the electron’s velocity to be $1460 \, \mathrm{m/s}$ , and the expression for kinetic energy from Physics 131: $K = \frac{1}{2} m v^2$ :

$K = \frac{1}{2} (9.11 \times 10^{-31} \, \mathrm{kg})(1460 \, \mathrm{m/s})^2$

$K = 9.64 \times 10^{-25} \, \mathrm{J} = 6.02 \times 10^{-6} \, \mathrm{eV}$

2. Directly use the fact that we already know the electron’s momentum from the previous problem $p = 1.33 \times 10^{-27} \, \mathrm{kg \cdot m/s}$ . Combine this knowledge and the idea of converting directly from momentum to energy for particles with mass using the formula derived in Some Energy-Related Ideas that Might be New: The Connection between Energy and Momentum:

$K = \frac{p^2}{2m}$

$K = \frac{(1.33 \times 10^{-27} \, \mathrm{kg \cdot m/s})^2}{2(9.11 \times 10^{-31} \, \mathrm{kg})} = 9.64 \times 10^{-25} \, \mathrm{J} = 6.02 \times 10^{-6} \, \mathrm{eV}$

Clearly, both approaches give the same response as they must.

The photon:

Again, there are two approaches:

1. Use the momentum of the photon to get the energy using $E_\gamma = pc$ :

$E_\gamma = pc$

$E_\gamma = ((1.33 \times 10^{-27} \, \mathrm{kg \cdot m/s})(3 \times 10^8 \, \mathrm{m/s})$

$E_\gamma = 3.99 \times 10^{-19} \, \mathrm{J} = 2.49 \, \mathrm{eV}$ .

Where eV are electron volts discussed in Units of Energy.

2. The second approach, is to use the wavelength, coupled with the expression we just derived / you learned in chemistry:

$E = \frac{hc}{\lambda}$

$E = \frac{(6.626 \times 10^{-34} \, \mathrm{J \cdot s})(3 \times 10^8 \, \mathrm{m/s})}{500 \times 10^{-9} \, \mathrm{m}}$

$E = 3.99 \times 10^{-19} \, \mathrm{J} = 2.49 \, \mathrm{eV}$ .

Again, both approaches give the same value, as they must.

Homework Problem

Problem 22: From momentum, calculate the wavelength and energy of a photon.

Photon Energies and the Electromagnetic Spectrum

A photon is a quantum of EM radiation whose momentum is related to its wavelength by $p = \frac{h}{\lambda}$ . Combined with the connection between a photon’s energy and momentum $E_\gamma = pc$ yields the energy-wavelength relationship $E = \frac{hc}{\lambda}$ .

All EM radiation is composed of photons. Figure 5 shows various divisions of the EM spectrum plotted against wavelength, frequency, and photon energy. Previously in this book, photon characteristics were alluded to in the discussion of some of the characteristics of UV, x rays, and γ-rays, the first of which start with frequencies just above violet in the visible spectrum. It was noted that these types of EM radiation have characteristics much different than visible light. We can now see that such properties arise because photon energy is larger at high frequencies.

The electromagnetic spectrum including energy — **Figure 5:** The EM spectrum, showing major categories as a function of photon energy in eV, as well as wavelength and frequency. Certain characteristics of EM radiation are directly attributable to photon energy alone.

Photons act as individual quanta and interact with individual electrons, atoms, molecules, and so on. The energy a photon carries is, thus, crucial to the effects it has. Table 1 lists representative submicroscopic energies in eV. When we compare photon energies from the EM spectrum in Figure 5 with energies in the table, we can see how effects vary with the type of EM radiation.

Table 1
Representative Energies for Submicroscopic Effects (Order of Magnitude Only)
Energy between outer electron shells in atoms	1 eV
Binding energy of a weakly bound molecule	1 eV
Energy of red light	2 eV
Binding energy of a tightly bound molecule	10 eV
Energy to ionize atom or molecule	10 to 1000 eV

Gamma rays

A form of nuclear and cosmic EM radiation, can have the highest frequencies and, hence, the highest photon energies in the EM spectrum. For example, a γ-ray photon with $\nu = 10^{21} \, \mathrm{Hz}$ has an energy $E=h \nu = 6.63 \times 10^{-13} \, \mathrm{J} = 4.14 \, \mathrm{MeV}$ . This is sufficient energy to ionize thousands of atoms and molecules, since only 10 to 1000 eV are needed per ionization. In fact, γ rays are one type of ionizing radiation, as are x rays and UV, because they produce ionization in materials that absorb them. Because so much ionization can be produced, a single γ-ray photon can cause significant damage to biological tissue, killing cells or damaging their ability to properly reproduce. When cell reproduction is disrupted, the result can be cancer, one of the known effects of exposure to ionizing radiation. Since cancer cells are rapidly reproducing, they are exceptionally sensitive to the disruption produced by ionizing radiation. This means that ionizing radiation has positive uses in cancer treatment as well as risks in producing cancer. However, the high photon energy also enables γ rays to penetrate materials, since a collision with a single atom or molecule is unlikely to absorb all the γ ray’s energy. This can make γ rays useful as a probe, and they are sometimes used in medical imaging.

X-rays

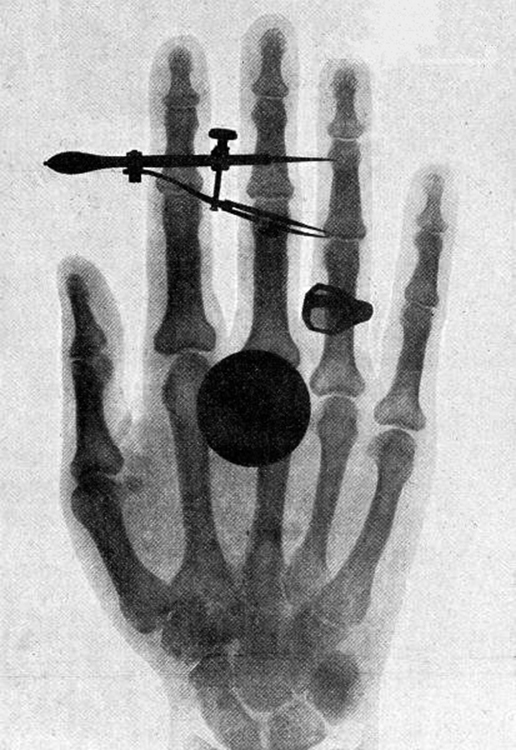
X-rays, as you can see in Figure 5, overlap with the low-frequency end of the γ ray range. Since x rays have energies of keV and up, individual x-ray photons also can produce large amounts of ionization. At lower photon energies, x rays are not as penetrating as γ rays and are slightly less hazardous. X-rays are ideal for medical imaging, their most common use, and a fact that was recognized immediately upon their discovery in 1895 by the German physicist W. C. Roentgen (1845–1923). (See Figure 6.) Within one year of their discovery, x rays (for a time called Roentgen rays) were used for medical diagnostics. Roentgen received the 1901 Nobel Prize for the discovery of x rays.

**Figure 6:** One of the first x-ray images, taken by Röentgen himself. The hand belongs to Bertha Röentgen, his wife. (credit: Wilhelm Conrad Röntgen, via Wikimedia Commons)

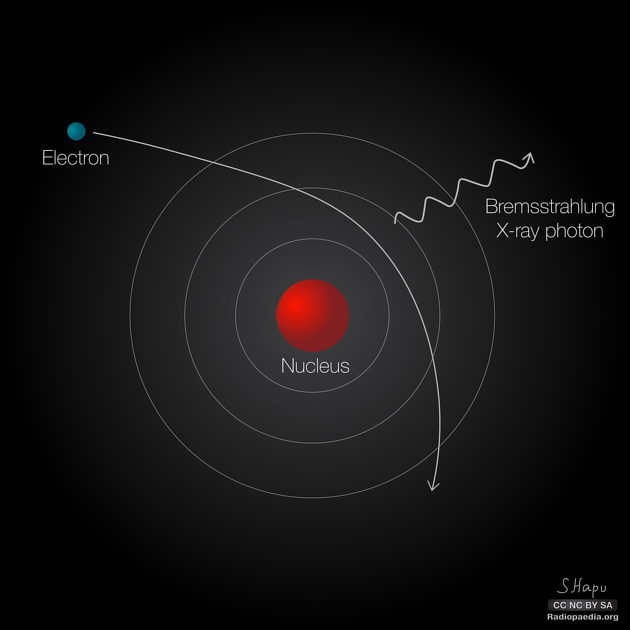
While γ rays originate in nuclear decay, x rays are produced by the process shown in Figure 7. Electrons ejected by thermal agitation from a hot filament in a vacuum tube are accelerated through a high voltage, gaining kinetic energy from the electrical potential energy. When they strike the anode, the electrons convert their kinetic energy to a variety of forms, including thermal energy. But since an accelerated charge radiates EM waves, and since the electrons act individually, photons are also produced. Some of these x-ray photons obtain the kinetic energy of the electron. The accelerated electrons originate at the cathode, so such a tube is called a cathode ray tube (CRT), and various versions of them are found in older TV and computer screens as well as in x-ray machines.

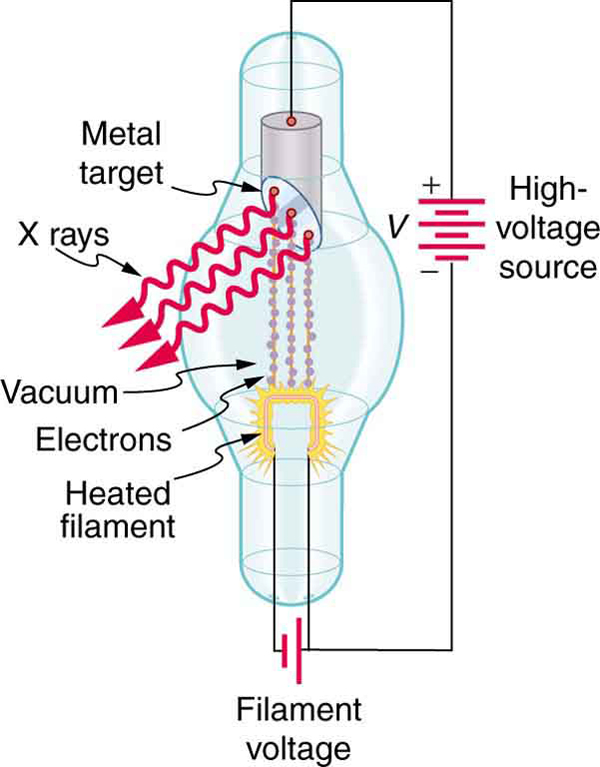
**Figure 7:** X rays are produced when energetic electrons strike the copper anode of this cathode ray tube (CRT). Electrons (shown here as separate particles) interact individually with the material they strike, sometimes producing photons of EM radiation.

Figure 8 shows the spectrum of x rays obtained from an x-ray tube. There are two distinct features to the spectrum. First, the smooth distribution results from electrons being decelerated in the anode material. A curve like this is obtained by detecting many photons, and it is apparent that the maximum energy is unlikely. This decelerating process produces radiation that is called bremsstrahlung (German for braking radiation). The second feature is the existence of sharp peaks in the spectrum; these are called characteristic x rays, since they are characteristic of the anode material. Characteristic x rays come from atomic excitations unique to a given type of anode material. They are akin to lines in atomic spectra, implying the energy levels of atoms are quantized.

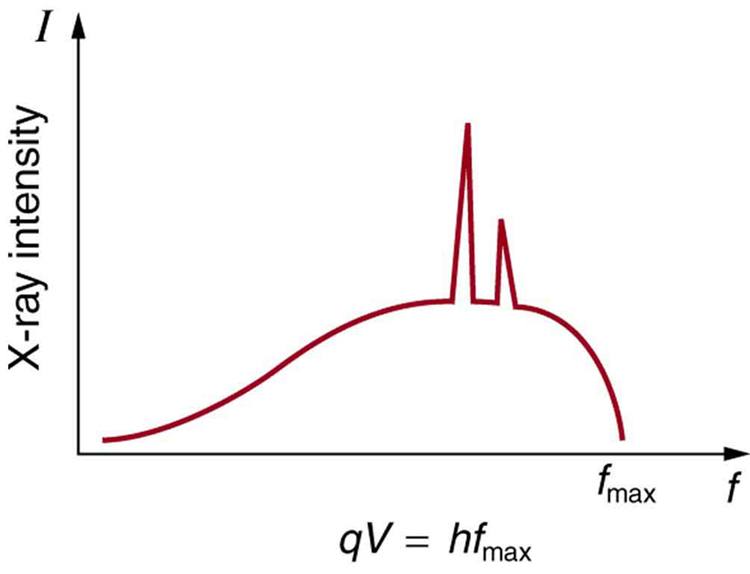
**Figure 8:** X-ray spectrum obtained when energetic electrons strike a material. The smooth part of the spectrum is bremsstrahlung, while the peaks are characteristic of the anode material. Both are atomic processes that produce energetic photons known as x-ray photons.

Connections: Conservation of Energy

Once again, we find that conservation of energy allows us to consider the initial and final forms that energy takes, without having to make detailed calculations of the intermediate steps.

Find the minimum wavelength of an x-ray photon produced by electrons accelerated through a potential energy difference of 50.0 keV in a CRT like the one in Figure 7.

Strategy

Electrons can give all of their kinetic energy to a single photon when they strike the anode of a CRT. The kinetic energy of the electron comes from electrical potential energy. Thus we can simply equate the maximum photon energy to the electrical potential energy

Solution

$\Delta E = Q + W$

$E_f - E_i = Q + W$

In the initial state, we have an electron with 50 keV of potential energy and no kinetic energy: $E_i = U_i = 50 \, \mathrm{keV}$ . At the end, all that energy is in the photon: $E_f = E_\gamma$ . No other energy enters or leaves the system (the photon and electron are everything we care about!), so $Q = W = 0$

$E_\gamma - U_i = 0$

$E_\gamma = U_i$

$\frac{hc}{\lambda} = U_i$

$\frac{1}{\lambda} = \frac{U_i}{hc}$

$\lambda = \frac{hc}{U_i}$

$\lambda = \frac{(6.626 \times 10^{-34} \, \mathrm{J \cdot s})(3 \times 10^8 \, \mathrm{m/s})}{(50 \times 10^3 \, \mathrm{eV}) \left( \frac{1.602 \times 10^{-19} \, \mathrm{J}}{\mathrm{eV}} \right)}$

$\lambda = 2.48 \times 10^{-11} \, \mathrm{m} = 0.025 \, \mathrm{nm}$

Ultraviolet Radiation

Ultraviolet radiation (approximately 4 eV to 300 eV) overlaps with the low end of the energy range of x rays, but UV is typically lower in energy. UV comes from the de-excitation of atoms that may be part of a hot solid or gas. These atoms can be given energy that they later release as UV by numerous processes, including electric discharge, nuclear explosion, thermal agitation, and exposure to x rays. A UV photon has sufficient energy to ionize atoms and molecules, which makes its effects different from those of visible light. UV thus has some of the same biological effects as γ-rays and x-rays. For example, it can cause skin cancer and is used as a sterilizer. The major difference is that several UV photons are required to disrupt cell reproduction or kill a bacterium, whereas single γ-ray and x-ray photons can do the same damage. But since UV does have the energy to alter molecules, it can do what visible light cannot. One of the beneficial aspects of UV is that it triggers the production of vitamin D in the skin, whereas visible light has insufficient energy per photon to alter the molecules that trigger this production. Infantile jaundice is treated by exposing the baby to UV (with eye protection), called phototherapy, the beneficial effects of which are thought to be related to its ability to help prevent the buildup of potentially toxic bilirubin in the blood.

Photon Energy and Effects for UV

Short-wavelength UV is sometimes called vacuum UV, because it is strongly absorbed by air and must be studied in a vacuum. Calculate the photon energy in eV for 100-nm vacuum UV, and estimate the number of molecules it could ionize or break apart.

Strategy

Using the equation $E= \frac{hc}{\lambda}$ and appropriate constants, we can find the photon energy and compare it with energy information in Table 1.

Solution

The energy of a photon is given by

$E= \frac{hc}{\lambda}$

Using hc=1240 eV⋅nm,

we find that

E=hc/λ=(1240 eV⋅nm)/100 nm=12.4 eV.

Discussion

According to Table 1, this photon energy might be able to ionize an atom or molecule, and it is about what is needed to break up a tightly bound molecule, since they are bound by approximately 10 eV. This photon energy could destroy about a dozen weakly bound molecules. Because of its high photon energy, UV disrupts atoms and molecules it interacts with. One good consequence is that all but the longest-wavelength UV is strongly absorbed and is easily blocked by sunglasses. In fact, most of the Sun’s UV is absorbed by a thin layer of ozone in the upper atmosphere, protecting sensitive organisms on Earth. Damage to our ozone layer by the addition of such chemicals as CFC’s has reduced this protection for us.

Visible Light

The range of photon energies for visible light from red to violet is 1.63 to 3.26 eV, respectively. These energies are on the order of those between outer electron shells in atoms and molecules. This means that these photons can be absorbed by atoms and molecules. A single photon can actually stimulate the retina, for example, by altering a receptor molecule that then triggers a nerve impulse. As reviewed from chemistry in a future chapter, photons can be absorbed or emitted only by atoms and molecules that have precisely the correct quantized energy step to do so. For example, if a red photon of frequency $\nu$ encounters a molecule that has an energy step, $\Delta E = h \nu$ , then the photon can be absorbed. Violet flowers absorb red and reflect violet; this implies there is no energy step between levels in the receptor molecule equal to the violet photon’s energy, but there is an energy step for the red.

There are some noticeable differences in the characteristics of light between the two ends of the visible spectrum that are due to photon energies. Red light has insufficient photon energy to expose most black-and-white film, and it is thus used to illuminate darkrooms where such film is developed. Since violet light has a higher photon energy, dyes that absorb violet tend to fade more quickly than those that do not. (See Figure 9.) Take a look at some faded color posters in a storefront some time, and you will notice that the blues and violets are the last to fade. This is because other dyes, such as red and green dyes, absorb blue and violet photons, the higher energies of which break up their weakly bound molecules. (Complex molecules such as those in dyes and DNA tend to be weakly bound.) Blue and violet dyes reflect those colors and, therefore, do not absorb these more energetic photons, thus suffering less molecular damage.

Photograph of a worn-out movie advertisement poster on a wall. — **Figure 9:** Why do the reds, yellows, and greens fade before the blues and violets when exposed to the Sun, as with this poster? The answer is related to photon energy. (credit: Deb Collins, Flickr)

Transparent materials, such as some glasses, do not absorb any visible light, because there is no energy step in the atoms or molecules that could absorb the light. Since individual photons interact with individual atoms, it is nearly impossible to have two photons absorbed simultaneously to reach a large energy step. Because of its lower photon energy, visible light can sometimes pass through many kilometers of a substance, while higher frequencies like UV, x-ray, and $γ$ rays are absorbed, because they have sufficient photon energy to ionize the material.

How Many Photons per Second Does a Typical Light Bulb Produce?

Assuming that 10.0% of a 100-W light bulb’s energy output is in the visible range (typical for incandescent bulbs) with an average wavelength of 580 nm, calculate the number of visible photons emitted per second.

Strategy

Power is energy per unit time, and so if we can find the energy per photon, we can determine the number of photons per second. This will best be done in Joules, since power is given in Watts, which are Joules per second.

Solution

The power in visible light production is 10.0% of 100 W, or 10.0 J/s. The energy of the average visible photon is found by substituting the given average wavelength into the formula

$E = \frac{hc}{\lambda}$

This produces

$E = \frac{ (6.63 \times 10^{-34} \, \mathrm{J \cdot s})(3.00 \times 10^8 \mathrm{m/s})}{580 \times 10^{-9} \, \mathrm{m}} = 3.43 \times 10^{-19} \, \mathrm{J}$ .

The number of visible photons per second is thus

$\frac{\mathrm{photon}}{\mathrm{s}} = \frac{10.0 \, \mathrm{J/s}}{3.43 \times 10^{-19} \, \mathrm{J/photon}}= 2.92 \times 10^{19} \, \mathrm{photon/s}$ .

Discussion

This incredible number of photons per second is verification that individual photons are insignificant in ordinary human experience. It is also a verification of the correspondence principle—on the macroscopic scale, quantization becomes essentially continuous or classical. Finally, there are so many photons emitted by a 100-W lightbulb that it can be seen by the unaided eye many kilometers away.

Lower Energy Photons

Infrared Radiation (IR)

Infrared radiation (IR) has even lower photon energies than visible light and cannot significantly alter atoms and molecules. IR can be absorbed and emitted by atoms and molecules, particularly between closely spaced states. IR is extremely strongly absorbed by water, for example, because water molecules have many states separated by energies on the order of $10^{–5} eV$ to $10^{–2} eV,$ well within the IR and microwave energy ranges. This is why in the IR range, skin is almost jet black, with an emissivity near 1—there are many states in water molecules in the skin that can absorb a large range of IR photon energies. Not all molecules have this property. Air, for example, is nearly transparent to many IR frequencies.

Microwaves

Microwaves are the highest frequencies that can be produced by electronic circuits, although they are also produced naturally. Thus microwaves are similar to IR but do not extend to as high frequencies. There are states in water and other molecules that have the same frequency and energy as microwaves, typically about $10^{–5} eV.$ This is one reason why food absorbs microwaves more strongly than many other materials, making microwave ovens an efficient way of putting energy directly into food.

Photon energies for both IR and microwaves are so low that huge numbers of photons are involved in any significant energy transfer by IR or microwaves (such as warming yourself with a heat lamp or cooking pizza in the microwave). Visible light, IR, microwaves, and all lower frequencies cannot produce ionization with single photons and do not ordinarily have the hazards of higher frequencies. When visible, IR, or microwave radiation is hazardous, such as the inducement of cataracts by microwaves, the hazard is due to huge numbers of photons acting together (not to an accumulation of photons, such as sterilization by weak UV). The negative effects of visible, IR, or microwave radiation can be thermal effects, which could be produced by any heat source. But one difference is that at very high intensity, strong electric and magnetic fields can be produced by photons acting together. Such electromagnetic fields (EMF) can actually ionize materials.

Misconception Alert: High-Voltage Power Lines

Although some people think that living near high-voltage power lines is hazardous to one’s health, ongoing studies of the transient field effects produced by these lines show their strengths to be insufficient to cause damage. Demographic studies also fail to show significant correlation of ill effects with high-voltage power lines. The American Physical Society issued a report over 10 years ago on power-line fields, which concluded that the scientific literature and reviews of panels show no consistent, significant link between cancer and power-line fields. They also felt that the “diversion of resources to eliminate a threat which has no persuasive scientific basis is disturbing.”

Lower Energy than Microwaves

It is virtually impossible to detect individual photons having frequencies below microwave frequencies, because of their low photon energy. But the photons are there. A continuous EM wave can be modeled as photons. At low frequencies, EM waves are generally treated as time- and position-varying electric and magnetic fields with no discernible quantization. This is another example of the correspondence principle in situations involving huge numbers of photons.

Homework Problems

Hint: Look carefully at the example above with the 100W light bulb!

Problem 23: An AM radio transmitter radiates some power at a given frequency. How many photons per second does the emitter emit?

Problem 24: If the brightness of a beam of light is increased, the ________ of the _____________ will also increase.

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Where Does Light Come From?

Properties of Light

The Main Parts of the Electromagnetic Spectrum

Introduction to the Photon

Photon Momentum – Relationship to Wavelength

Photon Momentum – Relationship to Energy

Photon Energies and the Electromagnetic Spectrum

Ionizing Radiation

Gamma rays

X-rays

Ultraviolet Radiation

Visible Light

Lower Energy Photons

Infrared Radiation (IR)

Microwaves

Lower Energy than Microwaves

License

Share This Book