22 Electric Fields
Introduction to Electric Field

Instructor’s Note
- Explain what a field is
- Explain how forces arise from objects interacting with field
- Justify the units of the electric field
For the past few units we have been really focusing on the ideas of light, now, everything we’ve been talking about in our units on geometric optics and physical optics applies to matter waves as well. We’ve just really been focusing on the applications to light. Now here in Unit 3, we will return two electrons, and these will be the focus of our attention for the next two units. Up to now, we’ve been ignoring the fact that electrons have charge, and we know that they do, so it’s time to fix that. By thinking about the charge attribute of electrons we will begin our study of the electric force.
To begin, I want to remind you from 131 that there are fundamentally only four forces: The strong nuclear force, which is responsible for holding all of the positively charged protons in the nucleus together. The electrical and magnetic forces, which we will see through this course are really two deeply connected sides of the same coin, and these are the ideas of opposite charges attract like charges repel and magnets.

Instructor’s Note
While these may seem like wildly different phenomena at first glance. We’ll see through this course that electricity and magnetism are deeply connected.
Next in strength we have the weak nuclear force responsible for radioactive decay, and then finally the gravitational force, which holds you to the Earth and holds the Earth in orbit around the Sun.
Gravity was talked about in some depth in Physics 131, whereas electricity and magnetism will consume our attention for the rest of 132. It’s worth pointing out that the idea of opposite charges attract and like charges repel is the fundamental origin of all of the other forces taught in these courses. For example, in 131, you discuss the normal force, when a physics book sits on a table you have the weight of the book, but you also have a normal force from the table on the book, which keeps it from falling through the table. This force is perpendicular, or normal, to the surface between the table in the book and really arises because of the electrons in the table repelling the electrons in the book.
Another force discussed in 131 is the idea of tension. For example, when a block is just hung by a string, you have the weight of the block being countered by the tension in the rope, but where does this tension ultimately come from? This tension comes from the atomic bonds which are fundamentally the electrical attraction between one molecule of rope and the next. Similarly, the spring force and Hooke’s law are a result of atomic bonds, which are electrical at the microscopic scale. Finally, the frictional forces arise from Van der Waals interactions between the molecules and different surfaces. Once again, you’re talking about the electrical interactions between atoms.
Before we begin with the electric field we’re going to explore everyone’s favorite number from Physics 131, this
![]()
that was used extensively in that course, and we’re going to deconstruct exactly what this number is. Gravity is a bit more familiar to us, as we experience it on a daily basis. And we will build up the idea of the electric field in parallel, using gravity as a crutch.

Instructor’s Note
It is important however to keep in mind that gravity and electricity are fundamentally different forces.
Absolutely everything in the universe experiences gravity. We saw in class, through our gravitational redshift of light, that even light experiences gravity. However only those objects with charges will experience electrical forces. Can you perhaps think of something that experiences gravity but not electricity? You would need something that has mass but not an electric charge.
Let’s begin thinking about gravity. We know that the force of gravity is what holds the moon in orbit around the Earth, but how does the moon know that the Earth is there? I mean the moon is ![]() meters away from the Earth. That’s a long way. How does the moon know that the Earth is even there? To simplify and bring it a little more down to Earth, no pun intended, we’re going to think about a ball. We all know that when I release a ball it falls due to the Earth’s gravity. We could ask the same question; how does the ball know that the Earth is there? They’re not in contact. Yes, the distances are a lot smaller, but they don’t touch each other. How does the ball know that the Earth is there?
meters away from the Earth. That’s a long way. How does the moon know that the Earth is even there? To simplify and bring it a little more down to Earth, no pun intended, we’re going to think about a ball. We all know that when I release a ball it falls due to the Earth’s gravity. We could ask the same question; how does the ball know that the Earth is there? They’re not in contact. Yes, the distances are a lot smaller, but they don’t touch each other. How does the ball know that the Earth is there?
The way that this is explained is that the Earth generates a gravitational field and this gravitational field is what the letter ![]() from Physics 131 represents, and the strength of that gravitational field is
from Physics 131 represents, and the strength of that gravitational field is ![]() Newton’s per kilogram. Now you might be used to thinking about it being meters per second squared but if you look a little bit at Newton’s second law,
Newton’s per kilogram. Now you might be used to thinking about it being meters per second squared but if you look a little bit at Newton’s second law, ![]() , you will see that meters per second squared and Newton’s per kilogram are equivalent units. We’re going to think in terms of Newton’s per kilogram, because it’s a more useful unit for our purposes right now.
, you will see that meters per second squared and Newton’s per kilogram are equivalent units. We’re going to think in terms of Newton’s per kilogram, because it’s a more useful unit for our purposes right now.
The Earth generates this gravitational field and it points straight down and it has a magnitude of ![]() Newton’s per kilogram. Now you will notice that the ball does actually touch the Earth’s gravitational field, it doesn’t touch the Earth, but it does touch this gravitational field. And through this contact the ball reacts to that field by feeling a gravitational force,
Newton’s per kilogram. Now you will notice that the ball does actually touch the Earth’s gravitational field, it doesn’t touch the Earth, but it does touch this gravitational field. And through this contact the ball reacts to that field by feeling a gravitational force, ![]() . The force is the mass of the ball,
. The force is the mass of the ball, ![]() , times the strength of the gravitational field,
, times the strength of the gravitational field, ![]() . That’s what gives rise to the force.
. That’s what gives rise to the force.
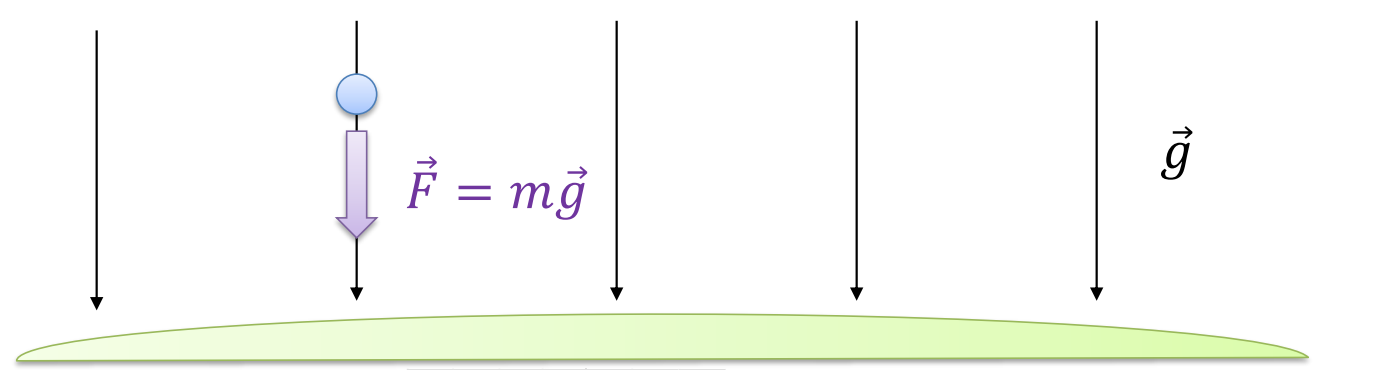
Now let’s return to these units for ![]() , these Newton’s per kilogram that you might not be used to thinking about. For every one kilogram of ball, the ball feels 9.8. Newton’s of force. That’s what
, these Newton’s per kilogram that you might not be used to thinking about. For every one kilogram of ball, the ball feels 9.8. Newton’s of force. That’s what ![]() means, a two-kilogram ball will feel 2 times 9.8 Newton’s of force. That’s why these units are somewhat useful for our purposes right now, is it tells us how many Newton’s of force we get for each kilogram of ball, that’s what 9.8 represents.
means, a two-kilogram ball will feel 2 times 9.8 Newton’s of force. That’s why these units are somewhat useful for our purposes right now, is it tells us how many Newton’s of force we get for each kilogram of ball, that’s what 9.8 represents.
Why did we introduce this middle step of a gravitational field that’s invisible and extends from the Earth? Why did we invent this? Why can’t we just say that something causes the ball to fall and the magnitude of the force is ![]() ? That’s what we did in 131.
? That’s what we did in 131.
Well the reason we invent this is because this field, while we cannot see, it is a fundamentally real object. It’s just as real as a ball. Yes, it’s invisible, but so are atoms, and you believe atoms are real so the field is a similar thing. It is fundamentally a real quantity, it contains energy, in fact we can think about the energy when we let the ball go. When the ball falls it gains kinetic energy, where does that energy come from? That energy comes from the gravitational field. This is a fundamentally different way of thinking a little more deeply about what gravity actually is and where this ![]() Newton’s per kilogram number comes from.
Newton’s per kilogram number comes from.
Now let’s return to the idea of electricity, the main focus of our course. How does the electron know the nucleus is there? We know that it’s the positively charged nucleus attracting the negatively charged electron that holds the atom together. But again, the nucleus and the electron do not touch, so how does the nucleus know that the electron is there? We’re going to add a proton to this situation for purposes of illustration, but the same argument can be made. How does this stray proton know that the nucleus is there?
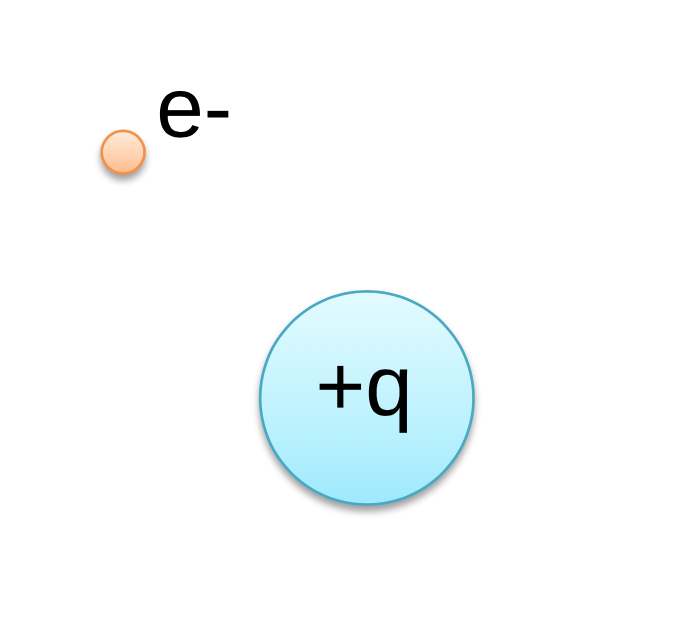
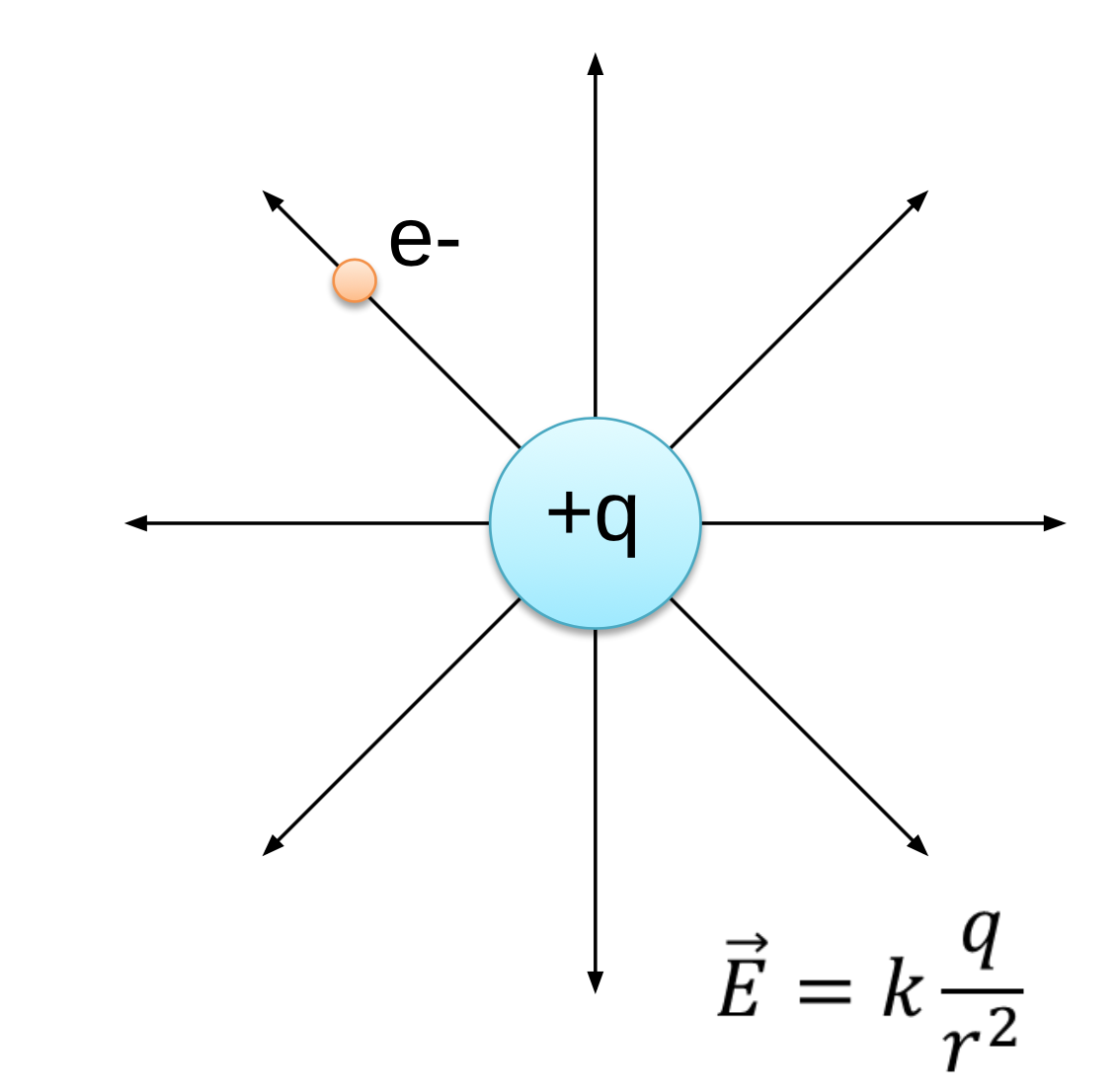
Well, we use the same sort of idea, the nucleus generates an electric field that we call ![]() and then the other charges, this electron and striped proton, respond to that field by feeling a force.
and then the other charges, this electron and striped proton, respond to that field by feeling a force.
The force felt by the electron is ![]() and, with analogy to gravity, where the force was the mass times the gravitational field, the force felt by these other charges is going to be the charge times the electric field. The stray proton feels a force
and, with analogy to gravity, where the force was the mass times the gravitational field, the force felt by these other charges is going to be the charge times the electric field. The stray proton feels a force ![]() , where
, where ![]() is the positive charge of proton, and similarly the electron also feels a force
is the positive charge of proton, and similarly the electron also feels a force ![]() , where now this
, where now this ![]() is the charge of the electron.
is the charge of the electron.
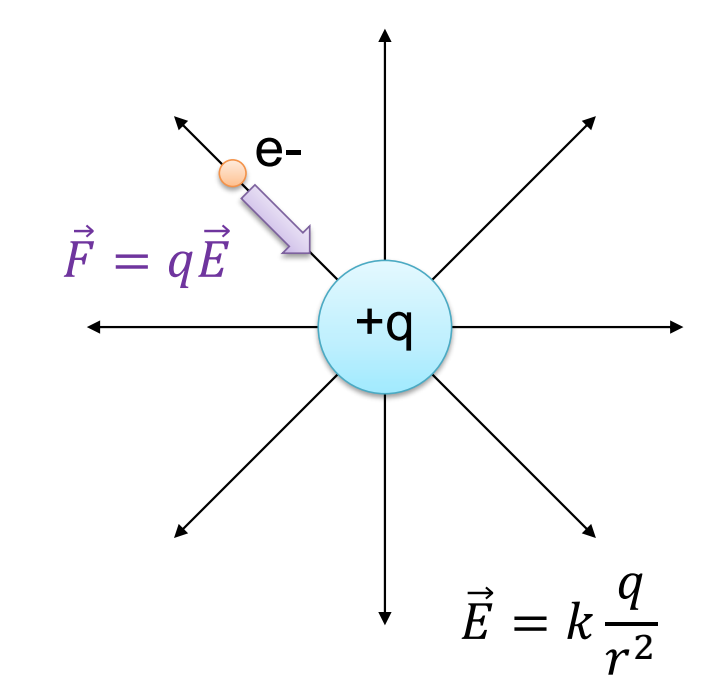
Now it’s worth noting that this expression gets the sign correct in the case of the proton. The charge is positive, and the force and the electric field are in the same direction. For the electron, the charge is negative and so the force and the electric field are in opposite directions, the force is inward, and the electric field is outwards. So, it’s important to keep in mind that this expression actually does get the signs correct, in fact so does our expression for gravity, mass is always positive and so the force of gravity is always in the same direction as the gravitational field. Once we know the forces we can then go on to calculate accelerations using Newton’s second law.
Let’s do some examples, we’ll do an example with gravity first, and then do one with electricity.
Gravitational Example
Let’s say we have a ![]() object with a charge of
object with a charge of ![]() and it’s sitting above the surface of the Moon where
and it’s sitting above the surface of the Moon where ![]() . Different planetary body different gravitational field. What is the acceleration of this five-kilogram object?
. Different planetary body different gravitational field. What is the acceleration of this five-kilogram object?
We begin by thinking about what force is acting, the weight force. We know that the weight force is the mass of the object times the gravitational field, in this case: ![]() times the
times the ![]() , giving us a weight force of
, giving us a weight force of ![]() .
.
Then we can move on to calculating the acceleration using Newton’s second law,
![]() .
.
The only force here is weight, the ![]() . We also know the mass of the ball
. We also know the mass of the ball ![]() , and we are left with the acceleration of
, and we are left with the acceleration of ![]() .
.

Instructor’s Note
Just as you might expect from 131 the acceleration and
![]()
are the same number. This results from the fact that both in the definition of the weight force and the definition of Newton’s second law are both dependent upon the mass of the object.
Electrical Example
Let’s go to electricity to see a case where it’s not always dependent upon mass.
Let’s have the same ![]() object with
object with ![]() of charge, only this time, it’s sitting in an electric field of
of charge, only this time, it’s sitting in an electric field of ![]() instead of a gravitational field of
instead of a gravitational field of ![]() . What is the acceleration in this case?
. What is the acceleration in this case?
Well the force at a play is now the electrical force which is going to be the electric charge times the electric field ![]() .
.
We know the charge is ![]() . We know the electric field is
. We know the electric field is ![]() , giving us an electric force of
, giving us an electric force of
![]() .
.
Now we move into calculating the acceleration, ![]() . Our force is
. Our force is ![]() , the electric force we just calculated. Our mass is
, the electric force we just calculated. Our mass is ![]() and so we get an acceleration of
and so we get an acceleration of
![]()
![]()
You’ll notice that in this case ![]() and
and ![]() are different: we have a
are different: we have a ![]() object with
object with ![]() of charge. The charge is what’s relevant for calculating the electric force, the mass is what’s relevant for calculating the acceleration, and since these are different the acceleration and the electric field are not the same number.
of charge. The charge is what’s relevant for calculating the electric force, the mass is what’s relevant for calculating the acceleration, and since these are different the acceleration and the electric field are not the same number.
This idea where the acceleration and the gravitational field are the same number is unique to gravity because both the force and Newton’s second law depend upon ![]() . This uniqueness, and thinking about it deeply, is what actually led Einstein to developing the general theory of relativity.
. This uniqueness, and thinking about it deeply, is what actually led Einstein to developing the general theory of relativity.

Instructor’s Note
I want you to work on visualizing these fields and thinking of interactions in terms of them.
The people who will be successful for the rest of this course will begin to really think about the fields as being real objects. These fields, gravitational fields, electric fields, magnetic fields, are truly present and they are everywhere around us.
This is how you “touch” things: the atoms in your finger never actually contact the atoms in the object you are touching. The charge in your finger generates an electric field, the charge in the wall interacts with that field and is repelled. That’s the origin of your sensation of pushing against the wall is through this intermediary of the electric field.


Instructor’s Note
Gravitational fields
- A distant object can interact with these fields and feel a force, an object with mass,
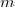 , in a gravitational field,
, in a gravitational field, 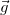 , feels a force,
, feels a force,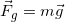 : mass times the field.
: mass times the field. - For gravity, the force
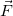 is always in the same direction as
is always in the same direction as 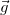 because mass is always positive.
because mass is always positive. - The units of
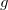 : we’re now going to think of them as Newton’s per kilogram.
: we’re now going to think of them as Newton’s per kilogram.
Electric fields
- An object with charge
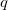 in electric field
in electric field 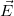 feels an electric force, charge times electric field,
feels an electric force, charge times electric field, 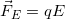 .
. - These parallels are what caused people to sometimes call mass gravitational charge, because mass is playing the same role for gravity as charge does for electricity.
- Unlike gravity, the force can be opposite the field because charge can be positive or negative, and just like the units of gravitational field are Newton’s per kilogram, the units of electric field are Newton’s per Coulomb.
Problem 6: Electrically neutral objects can exert a gravitational force on each other, but they cannot exert an electrical force on each other.
Problem 7: What is the magnitude of the force exerted on a 4.49 C charge by a 310.24 N/C electric field that points due east?
Problem 8: Find the direction and magnitude of an electric field that exerts a 9×10−17 N westward force on an electron.
Problem 9: Calculate the initial (from rest) acceleration of a proton in a 3.09×106 N/C electric field (such as created by a research Van de Graaff).
Problem 10: Suppose there is a single electron a set distance from a point charge Q, which quantities does the electric field experienced by the electron depend on?
Calculating an Electric Field from a Point Charge

Instructor’s Note
- Know that the quantity
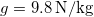 is a calculable quantity
is a calculable quantity - Be able to calculate the electric field from a given point charge.
In the last section, we discussed what electric fields are and how we visualize electrical forces in terms of electrical fields. In this section, we’re going to actually calculate them. Just as with the last section, we will be making use of gravity as an analogy.
Let’s begin by calculating fields and thinking in terms of gravity using our experience of Physics 131. Essentially the question we’re looking to answer is where does this ![]() come from?
come from?
The value ![]() is the strength of the gravitational field from the Earth at the surface of the Earth. If you are at the space station, which is just outside of the atmosphere, the value of
is the strength of the gravitational field from the Earth at the surface of the Earth. If you are at the space station, which is just outside of the atmosphere, the value of ![]() is a little bit smaller, it’s about
is a little bit smaller, it’s about ![]() . From this we can conclude that the strength of the gravitational field depends upon distance, the further you are from the planet, the weaker the gravitational field. On the moon on the other hand, the dominant gravitational field is not the gravitational field generated by the Earth, but the gravitational field generated by the moon and has a value of
. From this we can conclude that the strength of the gravitational field depends upon distance, the further you are from the planet, the weaker the gravitational field. On the moon on the other hand, the dominant gravitational field is not the gravitational field generated by the Earth, but the gravitational field generated by the moon and has a value of ![]() . In comparison, near the surface of the Sun, the dominant gravitational field is from the Sun and has a value of about
. In comparison, near the surface of the Sun, the dominant gravitational field is from the Sun and has a value of about ![]() . From this we can conclude that the strength of the gravitational field depends upon the mass of the object which is creating it. The moon is less massive than the Earth, so it generates a weaker gravitational field, the Sun is more massive than the Earth and generates a corresponding stronger gravitational field.
. From this we can conclude that the strength of the gravitational field depends upon the mass of the object which is creating it. The moon is less massive than the Earth, so it generates a weaker gravitational field, the Sun is more massive than the Earth and generates a corresponding stronger gravitational field.
It turns out that the strength of the gravitational field is actually calculable using the equation below.
![]()
Where ![]() is the mass of the object, which as we’ve already seen is one of the things that
is the mass of the object, which as we’ve already seen is one of the things that ![]() depends on, a more massive object will result in a larger gravitational field. It also depends upon the distance from the center,
depends on, a more massive object will result in a larger gravitational field. It also depends upon the distance from the center, ![]() , because as we’ve seen with a Space Station the further away we get, the smaller the strength of the gravitational field. And then this
, because as we’ve seen with a Space Station the further away we get, the smaller the strength of the gravitational field. And then this ![]() quantity is a constant of the universe, like the speed of light is a constant of the universe, and the value of this
quantity is a constant of the universe, like the speed of light is a constant of the universe, and the value of this ![]() constant is
constant is ![]() .
.

Instructor’s Note
You don’t actually need to know this expression for the gravitational field, I’m just using it to sort of build up an analogy because we’re more familiar with gravity.
But now let’s look at that analogy and think about calculating electric fields. Just as with gravitational fields, the strength of the electric field depends upon three things. The first being the amount of source, in this case the amount of charge that’s generating the electric field, not the amount of mass, and we indicate the amount of charge with the letter ![]() . Just as with gravitational fields, electric fields also decrease with distance from the center of the charge, and finally there is also a constant, this
. Just as with gravitational fields, electric fields also decrease with distance from the center of the charge, and finally there is also a constant, this ![]() constant
constant ![]() . When you go to write the formula for the electric field, it’s very similar to the formula for the strength of the gravitational field. Gravitational field was some constant mass over distance squared, electrical field is some constant charge over distance squared.
. When you go to write the formula for the electric field, it’s very similar to the formula for the strength of the gravitational field. Gravitational field was some constant mass over distance squared, electrical field is some constant charge over distance squared.
![]()

Instructor’s Note
I will ask you to use this particular equation.

Instructor’s Note
While the formula for gravitational fields and electric fields appear very similar, again I want to stress that you should keep in mind that electric fields and gravitational fields are completely different things, electric fields transmit electrical forces which act on anything with charge, gravitational fields act on anything with mass. An object with a mass and a charge will generate both a gravitational field and an electrical field.

Instructor’s Note
In class and in all of our examples I will use
![]()
and the reason for this is it will be easier in the long run when we talk about materials and light waves thinking in terms of
![]()
will be much more straightforward.
However, both ![]() and
and ![]() are on your equation sheet, in fact we have already seen the constant
are on your equation sheet, in fact we have already seen the constant ![]()
in one of our equations, the equation relating the amplitude of light to the intensity of light![]() , that’s the same
, that’s the same ![]() . And in fact, looking ahead, this
. And in fact, looking ahead, this ![]() in this equation stands for electric field. This is already starting to tell us something, that electric fields and light are going to be deeply connected in some interesting way that we’ll talk about in our last unit.
in this equation stands for electric field. This is already starting to tell us something, that electric fields and light are going to be deeply connected in some interesting way that we’ll talk about in our last unit.
Let’s move on and actually try to use this expression for calculating the electric fields and forces.
What is the strength of an electric field generated by an oxygen nucleus, which has ![]() protons in it, at a point
protons in it, at a point ![]() a distance of
a distance of ![]() ?
?
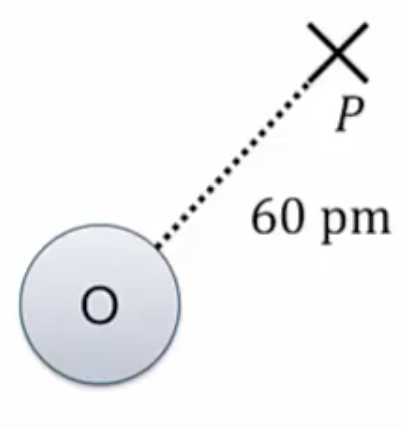
There is absolutely nothing currently at the point ![]() . We’re going to ignore the effects of all the surrounding electrons and just think about the nucleus for the moment. We begin with our definition for the strength of the electric field. It is the charges within the nucleus that are generating this field, and inside the nucleus we have
. We’re going to ignore the effects of all the surrounding electrons and just think about the nucleus for the moment. We begin with our definition for the strength of the electric field. It is the charges within the nucleus that are generating this field, and inside the nucleus we have ![]() protons, so we have
protons, so we have ![]() times the charge on each proton, giving us a total charge of
times the charge on each proton, giving us a total charge of ![]() . We also know that
. We also know that ![]() from the problem. When we plug in all of our numbers into the equation above we get an electric field of
from the problem. When we plug in all of our numbers into the equation above we get an electric field of ![]() .
.
Think about this for a second, the strength of the gravitational field generated by the entire Earth is essentially ![]() ! The electric fields inside of an atom are much larger. Since we know that the nucleus is positively charged we know that the electric field will point away from the source.
! The electric fields inside of an atom are much larger. Since we know that the nucleus is positively charged we know that the electric field will point away from the source.

Instructor’s Note
It’s worth pointing out that this field is a real thing and exists regardless if there is something to experience it at ![]() or not. The oxygen nucleus will generate a field that surrounds it which at point
or not. The oxygen nucleus will generate a field that surrounds it which at point ![]() has this value, respective of if there is actually an object at point
has this value, respective of if there is actually an object at point ![]() .
.
Now let’s see what happens when we put an object at point 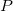
We’re going to go and add an electron at the point we’ve been talking about.
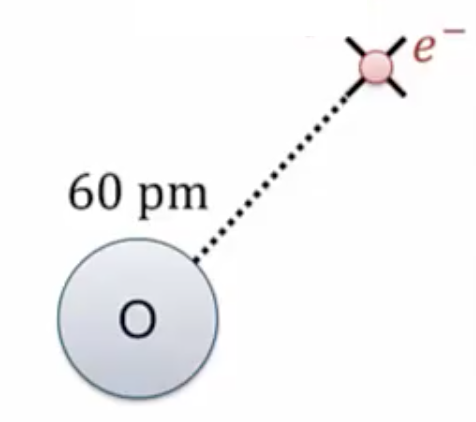
We know the strength of the electric field ![]() , calculated in the last part, we know that the electron will feel a force
, calculated in the last part, we know that the electron will feel a force
![]()
as discussed in a previous section, and we know the charge of the electron is ![]() . Substituting that charge and our value for electric field we get a force of
. Substituting that charge and our value for electric field we get a force of ![]() where the negative sign means that the force is opposite the electric field.
where the negative sign means that the force is opposite the electric field.
Then we can finally move on to calculating acceleration. We begin with Newton’s second law
![]()
The only force present on this particular electron is the electrical force, ![]() . We know the mass of the electron from our equation sheet 9.11×10-31 kilograms, and then we solve for the acceleration and we get an enormous value,
. We know the mass of the electron from our equation sheet 9.11×10-31 kilograms, and then we solve for the acceleration and we get an enormous value, ![]() . Remember for comparison, accelerations in your everyday life are 10 meters per second squared, and at an acceleration of about 80 meters per second squared you’re blacking out. This electron is accelerating with an astronomically large acceleration.
. Remember for comparison, accelerations in your everyday life are 10 meters per second squared, and at an acceleration of about 80 meters per second squared you’re blacking out. This electron is accelerating with an astronomically large acceleration.

Instructor’s Note
In Summary:
- The electric field from a point charge can be calculated by this
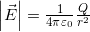 , which depends upon the charge, making the field make sense and the distance from the charge to the point of interest,
, which depends upon the charge, making the field make sense and the distance from the charge to the point of interest,  .
. - It also depends upon this constant
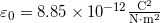 .
. - This field exists regardless if there is something there to feel it or not and the forces and fields in electricity we’ve already seen in the few examples are much bigger than gravitational forces.
- As sort of a reference point say you have two electrons, the electrical repulsion between the two electrons is
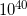 times larger than their gravitational attraction
times larger than their gravitational attraction
Problem 11: Calculate the magnitude of the electric field 8.41 m from a point charge of 8.92 mC (such as found on the terminal of a Van de Graaff).
Problem 12: What magnitude point charge creates a 15947.46 N/C electric field at a distance of 0.513 m? How large is the field at 18.85 m?
Visualizing Electric Fields
Drawings using lines to represent electric fields around charged objects are very useful in visualizing field strength and direction. Since the electric field has both magnitude and direction, it is a vector. Like all vectors, the electric field can be represented by an arrow that has length proportional to its magnitude and that points in the correct direction. (We have used arrows extensively to represent force vectors, for example.)
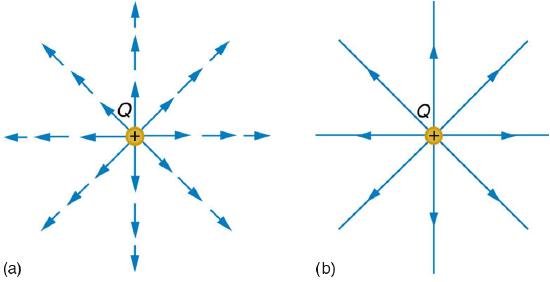
Figure 6 shows two pictorial representations of the same electric field created by a positive point charge Q. Figure 6b shows the standard representation using continuous lines. Figure 6a shows numerous individual arrows with each arrow representing the force on a test charge q. Field lines are essentially a map of infinitesimal force vectors.
In part a, electric field lines emanating from the charge Q are shown by the vector arrows pointing outward in every direction of two dimensional space. In part b, electric field lines emanating from the charge Q are shown by the vector arrows pointing outward in every direction of two dimensional space.
Note that the electric field is defined for a positive test charge q, so that the field lines point away from a positive charge and toward a negative charge. (See Figure 7.) The electric field strength is exactly proportional to the number of field lines per unit area, since the magnitude of the electric field for a point charge is ![]() and area is proportional to r2. This pictorial representation, in which field lines represent the direction and their closeness (that is, their areal density or the number of lines crossing a unit area) represents strength, is used for all fields: electrostatic, gravitational, magnetic, and others.
and area is proportional to r2. This pictorial representation, in which field lines represent the direction and their closeness (that is, their areal density or the number of lines crossing a unit area) represents strength, is used for all fields: electrostatic, gravitational, magnetic, and others.
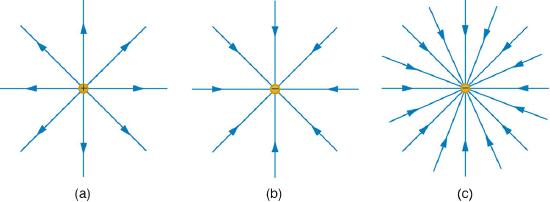
In part a, electric field lines emanating from a positive charge is shown by the vector arrows in all direction of two dimensional space and the density of these field lines is less. In part b, electric field lines entering the negative charge is shown by the vector arrows coming from all direction of two dimensional space and the density of these field lines is less. In part c, electric field lines entering the negative charge is shown by the vector arrows coming from all direction of two dimensional space and the density of these field lines is large.
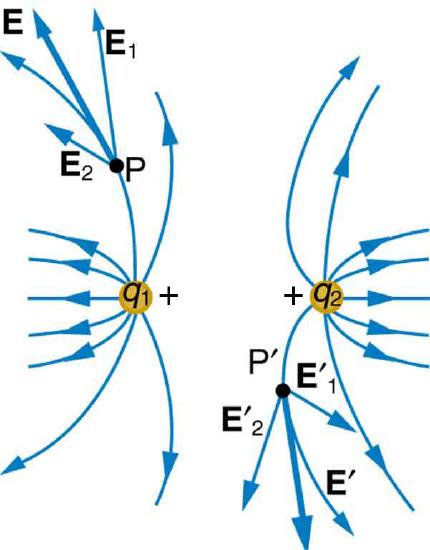
In many situations, there are multiple charges. The total electric field created by multiple charges is the vector sum of the individual fields created by each charge. Figure 10 shows how the electric field from two point charges can be drawn by finding the total field at representative points and drawing electric field lines consistent with those points. While the electric fields from multiple charges are more complex than those of single charges, some simple features are easily noticed. For example, the field is weaker between like charges, as shown by the lines being farther apart in that region. (This is because the fields from each charge point in opposite directions.) (See Figure 10 and Figure 11 (a).) Furthermore, at a great distance from two like charges, the field becomes identical to the field from a single, larger charge.
Two charges q one and q two are placed at a distance and their field lines shown by curved arrows move away from each other. At a point P on the field lines emanating from q one, the resultant electric field is represented by a vector arrow tangent to the curve representing this field line. A point P prime on a field line emanating from the charge q two and the resultant electric field is represented by a vector arrow tangent to the curve representing this field line.
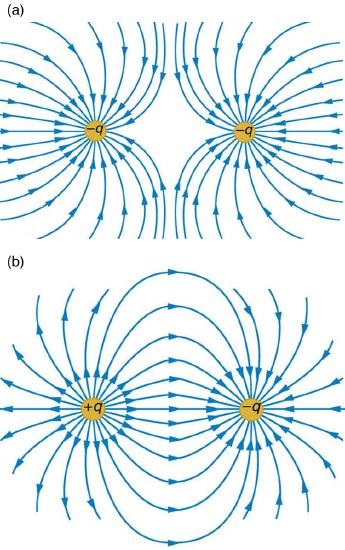
In part a, two negative charges of magnitude minus q are placed at some distance. Their field lines are represented by curved arrows terminating into the negative charges. The curves are divergent. In part b, two charges are placed at a distance where one is positive labeled as plus q and other is negative labeled as minus q. The field lines represented by curved arrows start from the positive charge and end at the negative charge. The curves are convergent.
We use electric field lines to visualize and analyze electric fields (the lines are a pictorial tool, not a physical entity in themselves). The properties of electric field lines for any charge distribution can be summarized as follows:
- Field lines must begin on positive charges and terminate on negative charges, or at infinity in the hypothetical case of isolated charges.
- The number of field lines leaving a positive charge or entering a negative charge is proportional to the magnitude of the charge.
- The strength of the field is proportional to the closeness of the field lines—more precisely, it is proportional to the number of lines per unit area perpendicular to the lines.
- The direction of the electric field is tangent to the field line at any point in space.
- Field lines can never cross.
The last property means that the field is unique at any point. The field line represents the direction of the field; so if they crossed, the field would have two directions at that location (an impossibility if the field is unique).

Instructor’s Notes
I will expect you to know these five rules.

