Basics of Particles

Roger Hinrichs; Paul Peter Urone; Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; Richard Langley; Julianne Zedalis; John Eggebrecht; E.F. Redish

3 Basics of Particles

What is a Particle?

What is a ? The simplest image of a particle is probably just a ball. What properties apply to all particles? We talked about particles a lot in Physics 131 in the point mass approximation, but it’s probably best that we flush out our definitions.

In its most generic sense, a particle is a chunk of stuff. It exists in a particular place and at a particular time and a particle doesn’t go around corners. If I throw a ball at a door, it’ll either go through the door or bounce back, it won’t curve around it. Particles can, but do not necessarily have to, have mass, we will talk about a massless particle in a later section. But all particles can be thought of as having momentum, that quantity from 131 of mass times velocity. Particles can also be thought of as having energy.

Instructor’s Note

In summary, you need to know that particles can be thought of as balls with defined position and speed and are characterized by:

Their energy $E$
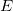
Their momentum $\vec{p}$
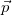
How many of them there are $N$

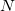
Linear Momentum and Force (Review from Physics 131)

This material is review from physics 131, but we will use these ideas in this unit, so here is a short refresher.

Instructor’s Note

You quiz will cover:

Calculate the momentum for any object
Recall that momentum is a vector
From the change in momentum, compute the average force

The scientific definition of linear momentum is consistent with most people’s intuitive understanding of momentum: a large, fast-moving object has greater momentum than a smaller, slower object. Linear momentum is defined as the product of a system’s mass multiplied by its velocity. In symbols, linear momentum is expressed as

$\vec{p}=m\vec{v}$ .

Momentum is directly proportional to the object’s mass and also its velocity. Thus the greater an object’s mass or the greater its velocity, the greater its momentum. Momentum p is a vector having the same direction as the velocity v. The SI unit for momentum is kg⋅m/s.

Example Calculating Momentum: A Football Player and a Football

(a) Calculate the momentum of a 110-kg football player running at 8.00 m/s.

(b) Compare the player’s momentum with the momentum of a hard-thrown 0.410-kg football that has a speed of 25.0 m/s.

Strategy

No information is given regarding direction, and so we can calculate only the magnitude of the momentum, p. In both parts of this example, the magnitude of momentum can be calculated directly from the definition of momentum given in the equation, which becomes

$p=mv$

when only magnitudes are considered.

Solution for (a)

To determine the momentum of the player, substitute the known values for the player’s mass and speed into the equation.

$p_{\mathrm{player}} = (110 \, \mathrm{kg}) (8.00 \, \mathrm{m/s}) =880 \, \mathrm{kg\cdot m/s}$

Solution for (b)

To determine the momentum of the ball, substitute the known values for the ball’s mass and speed into the equation.

$p_{\mathrm{ball}} = (0.410 \, \mathrm{kg})(25.0 \, \mathrm{m/s}) = 10.3 \, \mathrm{kg \cdot m/s}$

The ratio of the player’s momentum to that of the ball is

$\frac{p_{\mathrm{player}}}{p_{\mathrm{ball}}} = \frac{880}{10.3} = 85.9.$

Discussion

Although the ball has greater velocity, the player has a much greater mass. Thus the momentum of the player is much greater than the momentum of the football, as you might guess. As a result, the player’s motion is only slightly affected if he catches the ball.

Instructor’s Note

The example above is representative of what you will be asked to do on your homework and quizzes.

Homework

Problem 4: Compare the momenta of elephants, humans, and tranquilizer darts!

Momentum and Newton’s 2nd Law (Optional)

All you need to know from this section is the definition of momentum. The following connection to Newton’s 2nd Law is just to help you put this info into context.

The importance of momentum, unlike the importance of energy, was recognized early in the development of classical physics. Momentum was deemed so important that it was called the “quantity of motion.” Newton actually stated his second law of motion in terms of momentum: The net external force equals the change in momentum of a system divided by the time over which it changes. Using symbols, this law is

$\sum \vec{F} = \frac{\Delta \vec{p}}{ \Delta t}$ ,

where $\sum \vec{F}$ is the net external force, $\Delta \vec{p}$ is the change in momentum, and $\Delta t$ is the change in time.

Newton’s 2nd Law in Terms of Momentum

The net external force equals the change in momentum of a system divided by the time over which it changes.

$\sum \vec{F} = \frac{\Delta \vec{p}}{ \Delta t}$ ,

Making Connections: Force and Momentum

Force and momentum are intimately related. Force acting over time can change momentum, and Newton’s second law of motion, can be stated in its most broadly applicable form in terms of momentum. Momentum continues to be a key concept in the study of atomic and subatomic particles in quantum mechanics.

This statement of Newton’s second law of motion includes the more familiar $\sum \vec{F} = m \vec{a}$ as a special case. We can derive this form as follows. First, note that the change in momentum $\Delta p$ is given by

$\Delta p= \Delta (mv)$ .

If the mass of the system is constant, then

$\Delta (mv)=m \Delta v$ .

So that for constant mass, Newton’s second law of motion becomes

$\sum \vec{F} = \frac{\Delta \vec{p}}{\Delta t} =m \frac{\Delta \vec{v}}{ \Delta t}$ .

Because

$\frac{\Delta \vec{v}}{ \Delta t} = \vec{a}$ ,

we get the familiar equation

$\sum \vec{F} = m \vec{a}$

when the mass of the system is constant.

Newton’s second law of motion stated in terms of momentum is more generally applicable because it can be applied to systems where the mass is changing, such as rockets, as well as to systems of constant mass. We will consider systems with varying mass in some detail; however, the relationship between momentum and force remains useful when mass is constant, such as in the following example.

Example Calculating Force: Venus Williams’ Racquet

During the 2007 French Open, Venus Williams hit the fastest recorded serve in a premier women’s match, reaching a speed of 58 m/s (209 km/h). What is the average force exerted on the 0.057-kg tennis ball by Venus Williams’ racquet, assuming that the ball’s speed just after impact is 58 m/s, that the initial horizontal component of the velocity before impact is negligible, and that the ball remained in contact with the racquet for 5.0 ms (milliseconds)?

Strategy

This problem involves only one dimension because the ball starts from having no horizontal velocity component before impact. Newton’s second law stated in terms of momentum is then written as

$\sum F = \frac{ \Delta p}{ \Delta t }$ .

As noted above, when mass is constant, the change in momentum is given by

$\Delta p=m \Delta v=m(v_f−v_i)$ .

In this example, the velocity just after impact and the change in time are given; thus, once $\Delta p$ is calculated,

$\sum F= \frac{\Delta p}{ \Delta t}$

can be used to find the force.

Solution

To determine the change in momentum, substitute the values for the initial and final velocities into the equation above.

$\Delta p = m(v_f-v_i)(0.057 \, \mathrm{kg})(58 \, \mathrm{m/s} - 0 \, \mathrm{m/s}) = 3.306 \, \mathrm{kg \cdot m/s} \approx 3.3 \, \mathrm{kg \cdot m/s}$

Now the magnitude of the net external force can determined by using $\sum F= \frac{\Delta p}{ \Delta t}$ :

$\sum F= \frac{\Delta p}{ \Delta t} = \frac{3.306 \, \mathrm{kg \cdot m/s}}{5.0 \times 10^{−3} \, \mathrm{s}} = 661 \, \mathrm{N} \approx 660 \, \mathrm{N}$ ,

where we have retained only two significant figures in the final step.

Discussion

This quantity was the average force exerted by Venus Williams’ racquet on the tennis ball during its brief impact (note that the ball also experienced the 0.56-N force of gravity, but that force was not due to the racquet). This problem could also be solved by first finding the acceleration and then using $\sum \vec{F} =m \vec{a}$ , but one additional step would be required compared with the strategy used in this example.

Chapter Summary

Linear momentum (momentum for brevity) is defined as the product of a system’s mass multiplied by its velocity. In symbols, linear momentum 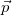$\vec{p}$ is defined to be 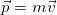$\vec{p}=m\vec{v}$ , where 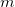$m$ is the mass of the system and 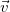$\vec{v}$ is its velocity.
The SI unit for momentum is kg⋅m/s.
Newton’s second law of motion in terms of momentum states that the net external force equals the change in momentum of a system divided by the time over which it changes. In symbols, Newton’s second law of motion is defined to be 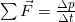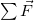$\sum \vec{F} =\frac{\Delta p}{\Delta t}$ , $\sum \vec{F}$ the net external force, 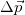$\Delta \vec{p}$ is the change in momentum, and 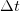$\Delta t$ is the change time.

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

What is a Particle?

Linear Momentum and Force (Review from Physics 131)

Momentum and Newton’s 2nd Law (Optional)

Chapter Summary

License

Share This Book