Unit I On-a-Page
Principles and Definitions
If you have had Dr. Toggerson or Dr. Bourgeois for Physics 131, you are familiar with a distinction made between principles and definitions. The are the fundamental rules of the Universe that describe how things work. Concepts which are , on the other hand, simply describe a quantity. For example,
is the definition of momentum for a massive particle; this equation offers no deep foundational insights on how the universe works. We physicists simply noted that the quantity 
came up a lot and we gave it a name 
. In order to describe how the Universe works, principles will often involve multiple definitions. Note, sometimes a principle or definition has an equation, other times it is just stated in words! This connects to Physics Goals 1 and 2 for this course.
To help get those of you who may not be used to this distinction acquainted and to help organize the huge amount of factual information in this particular unit, I will list the principles for this unit. You can quickly see how short this list is.
Principles for this Unit
Basic Properties of Light
- Light in a vacuum always travels at the speed of light
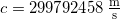
Basic Properties of Waves
- Fundamental connection between
, 
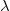, and wave speed 
: 
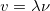
- The
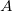is independent of frequency
Basics of Energy
- Energy is conserved. The change in
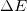is caused by the exchange of energy through 
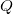and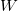 
: 
.
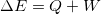Wave Particle Duality
- You can convert from the wave picture to the particle picture through the de Broglie relation:
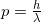where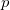 
is the momentum of the particle.
In chemistry, you probably saw the conversion between energy and wavelength for photons done through the equation 
. We will NOT be considering that as a principle to begin analyses / solving problems. The reason is that, in chemistry, you only considered converting between energy and wavelength for photons. We want to think about BOTH photons AND electrons. It turns out, that ONLY works for photons, while 
works for both photons and electrons! Thus we consider 
to be our principle. Many students get tripped up by applying to electrons. Don’t fall into this trap!- The probability of finding a particle in a given location is proportional to the square of the amplitude
.
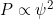- Increase amplitude by 3, probability goes up by 9.
- For light, we represent the amplitude not by 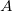but by
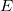. This is NOT the energy (confusing I know, but it is what it is). We will see why we use 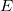later in the semester.
Standing Waves
- The wave must “fit” in the box or on the ring. For a box, this means that the box must be an integer number of 1/2 wavelengths
.
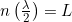Instructor’s Note
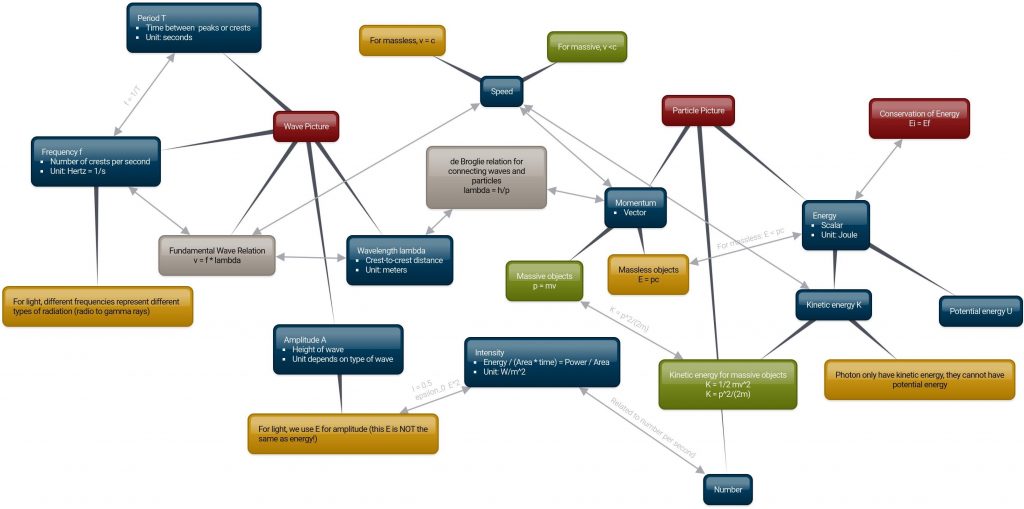
The ideas in this unit can be connected in many different ways. One possible useful way to organize such information is in a “concept map” like the one shown below. The map is also available at this link.
In this map:
- UMass maroon bubbles are big ideas
- Yellow bubbles apply to massless particles like light
- Green bubbles apply to massive particles like electrons
I would recommend printing a copy for use in class!
A fundamental relationship that describes how the Universe works. These are the fundamental truths of Nature. When writing a principle as an equation, the "=" is translated as "causes." For example, Newton's 2nd Law, F = ma, a force F causes an object m to accelerate (change its speed or direction) a. These principles are where we begin our analyses.
An equation representing a common quantity. This equation does not elucidate a fundamental truth of the Universe, it just defines an idea. For example, velocity = distance / time. There are no fundamental truths here, that is just the definition of velocity.
The distance from one point in a wave to the same point on the next wave: for example, crest-to-crest. This is a distance measured in meters.
The number of wave crests passing a point per second. The unit is 1/s or, equivalently, Hertz Hz.
The frequency will be 1 divided by the period T.
The size of the wave. For a physical wave like a water wave, this will be the actual height in meters. For a sound wave (a pressure wave in the air) this will be in units of pressure Pa.
From physics 131: The ability of an object to do work. I.e. its capability to exert a force for a distance. Whether that ability is realized is not relevant.
Energy comes, ultimately, in only two types: kinetic and potential. Kinetic energy is the capability to do work due to motion; thermal energy due to temperature, is at a fundamental level, kinetic energy due to molecular motion. Potential energy is the energy due to the relative positions of two objects: gravitational potential energy arises from the relative positions of an object and the Earth. "What is the gravitational potential energy of the ball?" is, technically, a meaningless question. The question only has relevance when considered in conjunction with the fact that the Earth exists.
The transfer of energy through microscopic collisions: fast moving (high-temperature) atoms colliding with slow moving (low-temperature) atoms results in the movement of energy from hot-to-cold.
Relevant to this course, the collisions could also be with photons.
The exchange of energy through the application of a force through some distance.
