10 Fundamentals of “Particle in a Box”

Boxes and Electrons in Atoms: The Essential Questions

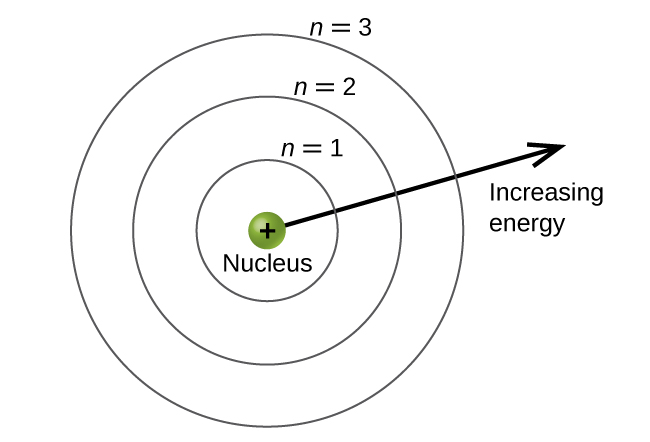
Our goal for this unit is to understand why electrons in atoms exist in discrete energy levels; you probably know from chemistry that they do. Typically, these discrete energy levels are depicted as in the figure below. The question we want to answer is, “WHY?” Why do electrons only have specific energies?

electrons in discrete energy levels
Electrons in atoms exist in discrete energy levels. Different shells are numbered by principal quantum numbers. Figure 6.19 in OpenStax Chemistry 2e.

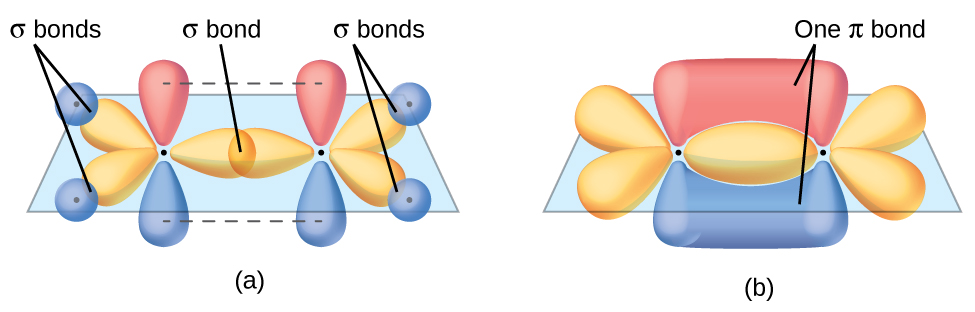
You have also probably been exposed in chemistry class to molecular orbital shapes like the one below. Again, we want to know “WHY?” Why do the orbitals for electrons in such molecules have these shapes? Can we predict what the orbitals will look like for different energy levels?

Hybridization of atomic orbitals into molecular orbitals.
In the ethene molecule, C2H4, there are (a) five σ bonds. One C–C σ bond results from overlap of sp2 hybrid orbitals on the carbon atom with one sp2 hybrid orbital on the other carbon atom. Four C–H bonds result from the overlap between the C atoms’ sp2 orbitals with s orbitals on the hydrogen atoms. (b) The π bond is formed by the side-by-side overlap of the two unhybridized p orbitals in the two carbon atoms. The two lobes of the π bond are above and below the plane of the σ system. Figure 8.23 in OpenStax Chemistry 2e.

To explore both of these sets of questions, we will investigate a simpler situation: what happens when you put an electron in a simple box. A box may not seem to have much in common with an atom at first glance, but we will see in class how these two situations are related.

Instructor’s Notes

What I want you to take away from this reading, are the specifics details of the box we will consider and how this impacts the particle-as-wave. These ideas will be the context of your homework problems and your in-class quiz. We will then use this model to understand why electrons have discrete energy levels and how we can predict the shapes of molecular orbitals.

The particulars of our box model

The following text is available as both video and text. The content is the same. Feel free to engage however suits you best.

 

Why do electrons in atoms have energy levels? You know they do from chemistry, right? Electrons exist in discrete energy levels. Why? To answer this we’re going to be physicists and do something simple and stupid first: we’re going to put a particle in a box. I know you’re thinking that sounds dumb, but it works! So, we’re going to put a particle in a box. In fact, we’re going to put it in a very special box:

  1. the box has only one dimension to it – it has a length 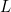L . The electron can only move along the box – it it can’t move in any other direction.
  2. the electron cannot got through the walls of the box – it cannot drill through them.

For those of you thinking this is unrealistic and goofy, long carbon chains act like this. Beta-carotene, those electrons act like they’re in a box very very well. Similarly, 1-3 butadiene, propene, etc.: for all of these, the electron in a box is a very good model.

The fact that the particle cannot drill through the walls tells us that the amplitude of the wave associated with the particle \psi must go to zero at the ends. As we will see in class, the amplitude \psi is related to the probability of finding the particle at a given spot. Since the electron cannot go through the walls, the amplitude must be zero at the ends. The result is a so-called standing wave just like the one on the string in the figure below: it is waving up and down, but goes to zero on both ends.

Possible standing waves on a string
For a string fixed on both ends, only certain waves, so-called standing waves, are possible as the wave must be zero on the ends. Figure 6.7 from OpenStax Chemistry 2e.

 

Examples

 

 

Key Takeaways

The key elements of our box model that I want you to take away are:

  • The box is one-dimensional: it has only a length 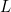L and no other dimensions.
    • Consequently, a particle in the box can only move along its length.
  • The walls of the box are such that the contained particle cannot “drill through” the walls.
    • Consequently, the amplitude 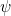\psi of the wave-aspect of the particle must be zero at both ends.
  • The waves on a string are a good way to visualize this.
  • While such a box may seem silly, it is a good model for many long organic molecules.

Homework Problems

Problem 28: Which graphs are allowed for a particle in a box.

 

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book