6 Basics of Waves

What is a Wave?

Now, we have talked about particles. What about waves? Before we start talking about waves, it’s probably best to give a few different examples of waves. If I ask you to think of a wave, the first thing that probably would come to most of your minds is a water wave, but we could also have waves on a string, or even sound waves. The most generic picture that a lot of you have is probably some sort of sine or cosine shape traveling along, but this is not representative of all waves, and we want our definition to be in terms of properties that apply to every possible wave that we can think of.

Let’s go through a few questions and develop a definition of a wave.

Does the wave actually have to go anywhere? Does a wave travel? No. Sure, most waves go somewhere; water waves travel across an ocean, for example. But think of a guitar string, when you pluck it, certainly the string waves back and forth, but the string doesn’t go anywhere. The wave stands on the string, which is called a standing wave. So, traveling cannot be part of our definition of a wave.

Does a wave have to be a repeating pattern? Again, not really. Although this image might be the one that comes to mind when I say the word ‘wave,’ remember that we can have just a single pulse going back and forth on a string.

Does the wave have to have up-and-down motion? Well again, no. The standard picture of a wave that you have in your head might look like Figure 1, but I could also send a compression wave down the slinky, like in Figure 2, where the links of the slinky move back and forth in the same direction as the wave’s motion.

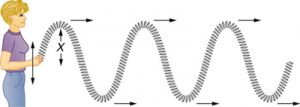
A transverse wave moving up and down perpendicular to the wave's motion on the slinky.
Figure 1. A wave can go up and down – a transverse wave. This is probably what you are picturing when I say wave.
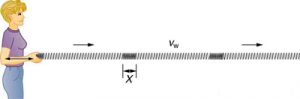
A compression or longitudinal wave down a slinky
Figure 2. A wave can go down the slinky as a compression – or longitudinal – wave.

Now, we need a little bit of terminology. Waves that do wiggle perpendicular to the direction of motion of the wave are called transverse waves. These are the waves that you probably have in mind, and these are the ones that we’re mostly going to be interested in.

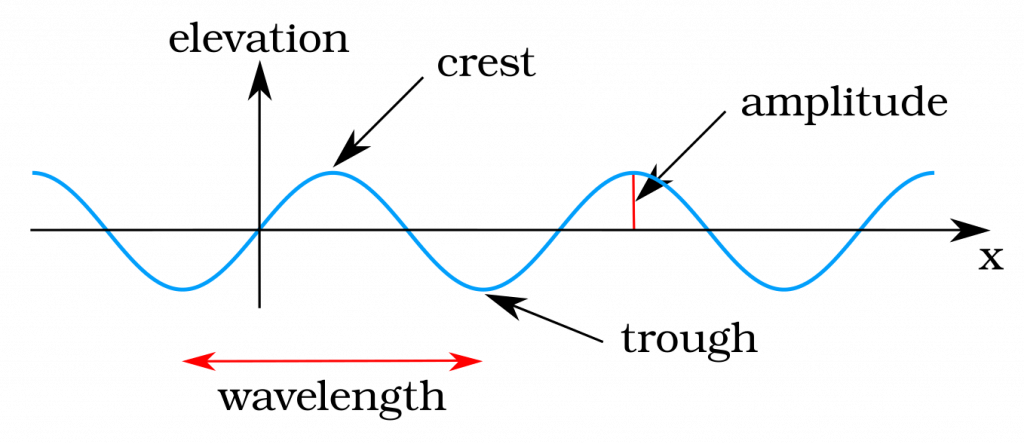
The basic terminology of transverse waves, which we’ll introduce some more later, is that waves have a peak and a trough, and then the distance from the zero line to either a peak or a trough is called the amplitude.

Figure 3. The parts of a wave from Kraaiennest, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons

What other properties of a wave could we perhaps use? Can a wave bend around corners? We know that particles don’t bend around corners, so what about waves? Well, it turns out that waves do bend around corners. Think of a water wave; it spreads out, bending around the corner.

Waves can bend around corners. Here we see water waves bending around the corners of a jetty.
Figure 4. Waves can bend around corners. Here we see water waves bending around the corners of a jetty. From Dmitris1, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

I go and just hit the water with a single stick, and we see waves coming out in all directions, radiating away from the spot where the dripping water from the bamboo trough hits the water, as shown in Figure 5 below.

Water dripping from a trough creates circular waves in still water.
Figure 5. Water dripping from a trough creates circular waves in still water. From https://www.pickpik.com/bamboo-water-liquid-nature-well-shallow-71547

 

Things get a little bit more interesting, however, if we have two sources of waves going at the same time next to each other, like so. Now, we get two waves, each radiating out from its source. In some places, the waves line up peak to peak or trough to trough, and add up, resulting in a larger wave at that point, as visible below. This is called constructive interference.

Constructive interference comes when waves line up peak to peak.
Figure 6. Constructive interference comes when waves line up peak to peak. This image is from Pixabay and was published prior to July 2017 under the Creative Commons CC0 1.0 Universal Public Domain Dedication license https://web.archive.org/web/20161229043156/https://pixabay.com/en/service/terms/ . In July 2017, Pixabay switched the old sitewide license for all uploads from Creative Commons CC0 to a custom license arrangement that does not meet the Creative Commons CC0 1.0 Universal Public Domain Dedication license terms.

In other places, the peak of one wave meets the trough of the other, resulting in some cancellation as visible below. This is called destructive interference.

Destructive interference comes when waves line up peak to trough.
Figure 7. Destructive interference comes when waves line up peak to trough. This image is from Pixabay and was published prior to July 2017 under the Creative Commons CC0 1.0 Universal Public Domain Dedication license https://web.archive.org/web/20161229043156/ https://pixabay.com/en/service/terms/. In July 2017, Pixabay switched the old sitewide license for all uploads from Creative Commons CC0 to a custom license arrangement that does not meet the Creative Commons CC0 1.0 Universal Public Domain Dedication license terms.

This interference phenomenon, where waves add in some places and cancel in others, is a characteristic property of waves.

So, what is a wave? Well, a wave is a disturbance that can, but doesn’t necessarily have to, travel, or it can just store energy and momentum. A traveling wave will carry energy from one position to another, think of the water wave that carries energy as it moves across the ocean and also momentum, as that wave hits you, you feel the momentum of the wave. For a standing wave, that energy is just being stored. When I pluck a guitar string, the energy is just being stored in the string and then ultimately releases as the sound that we hear. A wave need not necessarily repeat; we can have simple pulse waves. But, a wave can bend around corners, and waves of the same kind can interact with each other or with themselves, adding in some places and canceling in other places, through this idea of interference. These are the fundamental characteristics of waves. They don’t exist at a particular place; they sort of spread out over a couple of different places, and they can carry energy and momentum while bending around corners and interacting with themselves or other waves of the same kind.

Instructor’s Notes

 

To Summarize:

  • Particles are localized in space; they don’t bend around corners, but can carry energy and momentum.
  • Waves, on the other hand, are spread out in space; they are some kind of disturbance that can transfer or store energy and momentum.
  • However, waves, unlike particles, can bend around corners; waves can also interact with themselves or other waves of the same kind through this phenomenon of interference.

Period and Frequency in Oscillations

Close-up of a vibrating guitar string
Figure 8. The strings on this guitar vibrate at regular time intervals. (credit: JAR)

When you pluck a guitar string, the resulting sound has a steady tone and lasts a long time. Each successive vibration of the string takes the same time as the previous one. We define periodic motion to be a motion that repeats itself at regular time intervals, such as exhibited by the guitar string or by an object on a spring moving up and down. The time to complete one oscillation remains constant and is called the period 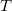T. Its units are usually seconds, but may be any convenient unit of time. The word period refers to the time for some event, whether repetitive or not, but we shall be primarily interested in periodic motion, which is by definition repetitive.

A concept closely related to period is the frequency of an event. For example, if you get a paycheck twice a month, the frequency of payment is 2 per month, and the period between checks is half a month. Frequency \nu is defined to be the number of events per unit time. For periodic motion, frequency is the number of oscillations per unit time. The relationship between frequency and period is

\nu = \frac{1}{T} .

 

The SI unit for frequency is the cycle per second, which is defined to be a hertz (Hz):

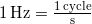1 \, \mathrm{Hz} = \frac{1 \, \mathrm{cycle}}{\mathrm{s}} or 1 \, \mathrm{Hz} = \frac{1}{s}

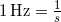
A cycle is one complete oscillation. Note that a vibration can be a single or multiple event, whereas oscillations are usually repetitive for a significant number of cycles.

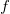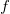A Venn-diagram showing the different sciencesThe different sciences use different symbols for frequency. If you have seen waves in a physics course before, they probably used the symbol f. However, in your chemistry classes, you probably used \nu. Both are in use and mean the same quantity. We will, in general, stick to using the \nu you used in chemistry, but don’t worry if you see an f used somewhere in your homework or in the text, it means the same quantity.

Fun with the history of science, different disciplines discovered the same quantity and gave it different names!

Determine the Frequency of Two Oscillations: Medical Ultrasound and the Period of Middle C

We can use the formulas presented in this module to determine both the frequency based on known oscillations and the oscillation based on a known frequency. Let’s try one example of each.

(a) A medical imaging device produces ultrasound by oscillating with a period of 0.400 µs. What is the frequency of this oscillation?

(b) The frequency of middle C on a typical musical instrument is 264 Hz. What is the time for one complete oscillation?

Strategy

Both questions (a) and (b) can be answered using the relationship between period and frequency. In question (a), the period 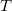T is given and we are asked to find frequency \nu. In question (b), the frequency \nu is given and we are asked to find the period T.

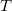Solution (a):

Substitute 0.400μs for T in 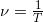\nu = \frac{1}{T} :

\nu = \frac{1}{T} = \frac{1}{0.400×10^{−6} \, \mathrm{s}} .

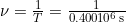Solve to find

\nu = 2.50×10^6 \, \mathrm{Hz}

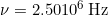
Discussion (a):

The frequency of sound found in (a) is much higher than the highest frequency that humans can hear and, therefore, is called ultrasound. Appropriate oscillations at this frequency generate ultrasound used for noninvasive medical diagnoses, such as observations of a fetus in the womb.

 

Solution (b):

Identify the known values:

The time for one complete oscillation is the period T:

\nu = \frac{1}{T} .

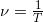Solve for T:

T = \frac{1}{\nu} .

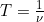Substitute the given value for the frequency into the resulting expression:

T = \frac{1}{264\, \mathrm{Hz}}

T = 3.79×10^{−3} \, \mathrm{s}=3.79 \, \mathrm{ms} .

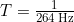
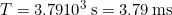Discussion (b)

The period found in (b) is the time per cycle, but this value is often quoted as simply the time in convenient units (ms or milliseconds in this case).

Everyday Periods and Frequencies

Identify an event in your life (such as receiving a paycheck) that occurs regularly. Identify both the period and frequency of this event.

Solution

I visit my parents for dinner every other Sunday. The frequency of my visits is 26 per calendar year. The period is two weeks.

Section Summary

  • Periodic motion is a repetitious oscillation.
  • The time for one oscillation is the period T.
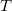  • The number of oscillations per unit time is the frequency \nu (or sometimes f).
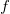  • These quantities are related by \nu = \frac{1}{T} .

Homework

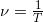Problem 11: What is the frequency of a stroboscope?

If you are curious about what a stroboscope is, check out The Stroboscope Wikipedia page.

Detailed description of a wave

Let’s begin by thinking about the one thing we have already figured out, which is that light has some wave-like properties. In the figure below, we have a wave, and we can talk about the wavelength, 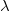\lambda, which is the distance from one point on the wave through the same point, as shown in Figure 9. Wavelength could be from peak to peak, from zero to zero, or from trough to trough. All those distances are the same, and the wavelength is measured in meters.

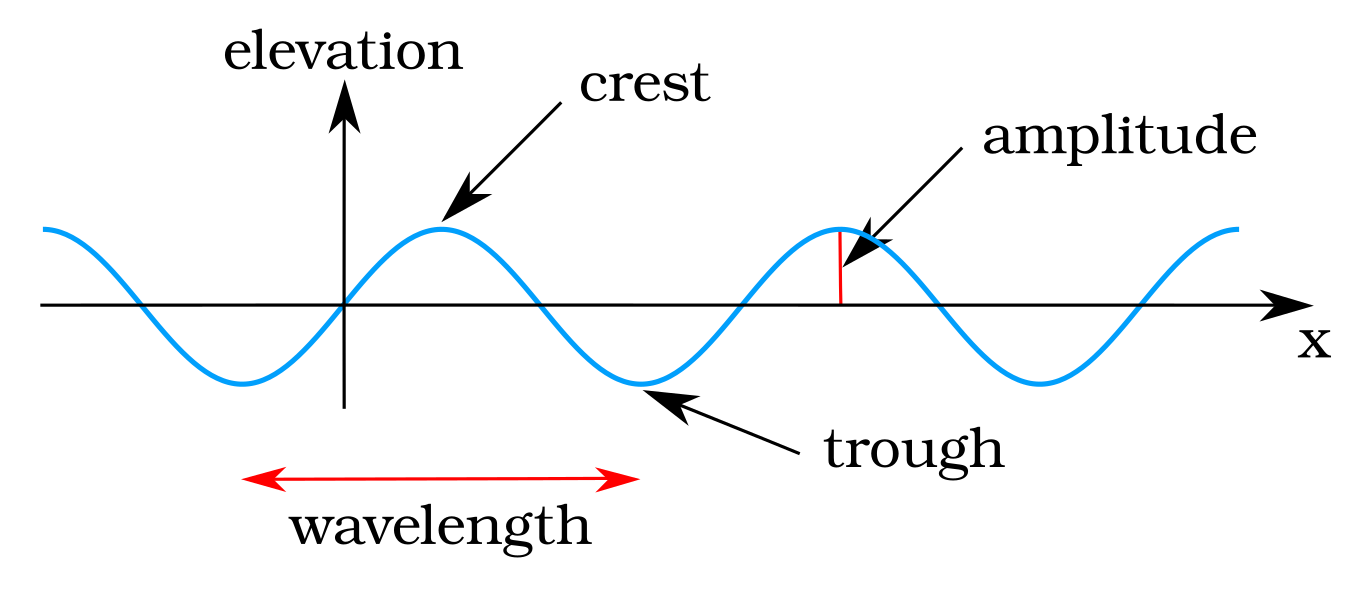
The parts of a wave.
Figure 9. The parts of a wave from Kraaiennest, CC BY-SA 3.0, via Wikimedia Commons

We also have the idea of the amplitude 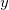y in the figure. The difference from either peak to the middle average or from trough to the middle average is what we call the amplitude.

In addition to wavelength and amplitude, we can also talk about how long it takes for a point to go up and down. Think about one point on the wave, bouncing up and down. We can talk about how long it takes for that point on the wave to go from trough to peak to trough; the amount of time it takes is called the period, 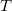T, and, as discussed in the last section, will be measured in seconds.

For this class, we will work in SI, International System of Units; we will not work in what I call barbaric units, there shall be no inches. Meters, kilograms, and seconds will be the norm. On the Moodle page, there’s a document of math I expect you to know, it’s things like trigonometry and area of a circle, but I also expect you to know the SI prefixes Nano – Giga. I will not give you these, and on an exam, if you come to the TAs and ask how big a micrometer is, we’re going to have to say “Tough cookie, that’s something you were supposed to know.”

The period is the time it takes for a point on the wave to go up and down, measured in seconds, but I can also count how many times that point oscillates in one second. I could ask, How many oscillations per second does this point on this wave make? That quantity, again looking back to the last section, is known as the frequency \nu and its value is

\nu = \frac{1}{T} ,

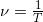the unit of frequency is how many per second or one over seconds, which is called Hertz: Hz.

We will use these basic terms for all of the waves we discuss: electrons and light. We know that wavelength is measured in meters, and we know that frequency is in Hertz, or 1 over seconds, so 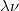\lambda \nu will be meters over seconds, which is a velocity. What’s the only velocity that we could have? The speed of the wave is the only speed we could talk about, so we have the speed of the wave as

v = \lambda \nu

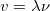
Exploring v = λν

If we know that the speed of a wave is fixed, for example, light travels at a fixed speed, then if the frequency goes up, what’s the wavelength going to do?

Solution:

We know that

v = \lambda \nu .

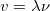The speed is fixed; if the frequency goes up, and 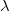\lambda times \nu has to be the same thing, then that is going to tell me that the wavelength must go down.

Discussion:

This question is based on mathematical reasoning using symbols, not numbers. Remember, one of the goals for this course was working in symbols and not numbers, so here’s an example of that.

Homework

Problem 12: Label the parts of a wave.

Problem 13: If the frequency of a wave is changed, which of the other properties must also change, assuming the speed of the wave remains fixed?

Problem 14: Speed, wavelength, and frequency for sound.

Energy in Waves: Intensity

Instructor’s Notes

 

The key takeaways that you will be potentially quizzed on are:

  • Intensity is power per area: 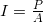I = \frac{P}{A} with units W/m2
  • The intensity is related to the square of the amplitude I \propto A^2

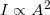
The energy effects of a wave depend on time as well as amplitude. For example, the longer deep-heat ultrasound is applied, the more energy it transfers. Waves can also be concentrated or spread out. Sunlight, for example, can be focused to burn wood. Earthquakes spread out, so they do less damage the farther they get from the source. In both cases, changing the area the waves cover has important effects. All these pertinent factors are included in the definition of intensity 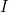I as power per unit area:

I = \frac{P}{A}

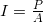
where 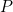P is the power carried by the wave through area 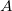A . The definition of intensity is valid for any energy in transit, including that carried by waves. The SI unit for intensity is watts per square meter (W/m2). For example, infrared and visible energy from the Sun impinge on Earth at an intensity of 1300 W/m2 just above the atmosphere.

Calculating intensity and power: How much energy is in a ray of sunlight?

The average intensity of sunlight on Earth’s surface is about 700 W/m2.

(a) Calculate the amount of energy that falls on a solar collector having an area of 0.500m2 in 4 hours.

(b) What intensity would such sunlight have if concentrated by a magnifying glass onto an area 200 times smaller than its own?

Strategy (a)

Because power is energy per unit time or

P = E/t

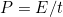
the definition of intensity can be written as

I = \frac{P}{A} = \frac{E}{t A}

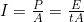
and this equation can be solved for E with the given information.

Solution (a)

  1. Begin with the equation that states the definition of intensity:
    I = \frac{P}{A}
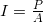
  2. Replace
    P with its equivalent E/t: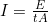
    I = \frac{E}{tA}
  3. Solve for E:
    E = I A t
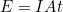
  4. Substitute known values into the equation:
    E = (700 \, \mathrm{W/m^2} )(0.5 \, \mathrm{m^2})(4 \, \mathrm{hr} \times 3600 \, \mathrm{s/hr})
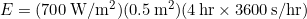
  5. Calculate to find E:
    E = 5.04 \times 10^6 \, \mathrm{J} = 5.04 \, \mathrm{MJ}

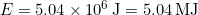
Discussion (a)

The energy falling on the solar collector in 4 hours is enough to be useful—for example, for heating a significant amount of water.

Strategy (b)

Taking a ratio of new intensity to old intensity and using primes for the new quantities, we will find that it depends on the ratio of the areas. All other quantities will cancel.

Solution (b)

  1. Take the ratio of intensities, which yields:
    \frac{I'}{I} = \frac{P'/A'}{P/A} = \frac{A}{A'}
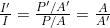
    The powers cancel because, as the source is always the sun, the power (energy per time) is the same: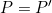 P = P'
  2. Identify the knowns:
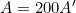    A = 200 A' as the area of the magnifying glass is 200x smaller.
    \frac{I}{I'} = \frac{200 A'}{A'} = 200
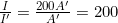
  3. Substitute known quantities:
    I' = 200 I
    I = 200 (700 \, \mathrm{W/m^2}
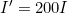
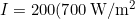
  4. Calculate to find:
    I' = 1.40 \times 10^5 \, \mathrm{W/m^2}

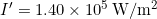
Discussion (b)

Decreasing the area increases the intensity considerably. The intensity of the concentrated sunlight could even start a fire.

Determine the combined intensity of two waves: Perfect constructive interference

If two identical waves, each having an intensity of 1.00 W/m2, line up perfectly peak-to-peak, what is the intensity of the resulting wave?

Strategy

If two waves, which have equal amplitudes 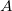A , line up exactly, the resulting wave has an amplitude of 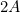2A . Because a wave’s intensity is proportional to amplitude squared, the intensity of the resulting wave is 4 times as great as that of the individual waves.

Solution

  1. Recall that intensity is proportional to amplitude squared.
  2. Calculate the new amplitude:
    I' \propto {A'}^2
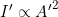
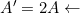    A' = 2A \leftarrow The new amplitude is twice the original
    I' \propto {2A}^2 = 4A
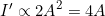
  3. Recall that the intensity of the old amplitude was: I \propto A^2
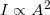
  4. Take the ratio of new intensity to the old intensity. This gives:
    \frac{I'}{I} = \frac{4A}{A} = 4
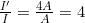
  5. Calculate to find I'
    I' = 4 I
    I' = 4 (1 \, \mathrm{W/m^2} = 4 \, \mathrm{W/m^2}

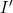
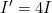
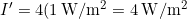
Discussion

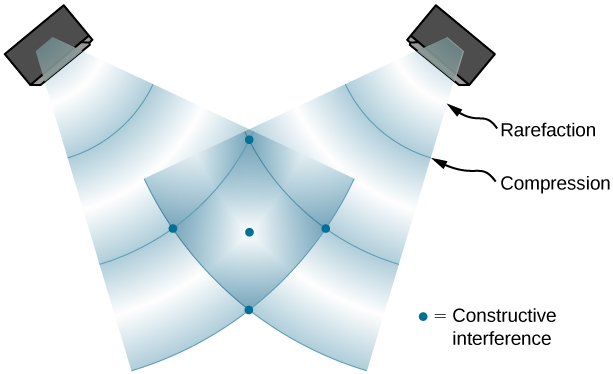
The intensity goes up by a factor of 4 when the amplitude doubles. This answer is a little disquieting. The two individual waves each have intensities of I.00 W/m2, yet their sum has an intensity of 4.00 W/m2, which may appear to violate conservation of energy. This violation, of course, cannot happen. What does happen is intriguing. The area over which the intensity is 4.00 W/m2 is much less than the area covered by the two waves before they interfered. For each spot where the waves line up peak-to-peak, there is somewhere else where they line up peak-to-trough and cancel. For example, if we have two stereo speakers putting out I.00 W/m2 each, there will be places in the room where the intensity is 4.00 W/m2 and other places where the intensity is zero, and other places where the intensity is in between. Figure 10 shows what this interference might look like.

The sound from two speakers adds constructively in some regions, yielding louder sound, and destructively in others yielding a quieter sound.
Figure 10. The sound from two speakers adds constructively in some regions, yielding louder sound, and destructively in others, yielding a quieter sound. From OpenStax University Physics, CC BY 4.0 https://creativecommons.org/licenses/by/4.0, via Wikimedia Commons.

Homework

Problem 15: How long to collect a certain amount of sunlight?

Problem 16: What is the power output of an ultrasound machine for a given intensity and area?

 

 

License

Icon for the Creative Commons Attribution 4.0 International License

Physics 132: What is an Electron? What is Light? by Roger Hinrichs, Paul Peter Urone, Paul Flowers, Edward J. Neth, William R. Robinson, Klaus Theopold, Richard Langley, Julianne Zedalis, John Eggebrecht, and E.F. Redish is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book