Unit I On-a-Page
Principles and Definitions
If you have had Dr. Toggerson or Dr. Bourgeois for Physics 131, you are familiar with a distinction made between principles and definitions. The are the fundamental rules of the Universe that describe how things work. Concepts which are , on the other hand, simply describe a quantity. For example,
![]()
is the definition of momentum for a massive particle; this equation offers no deep foundational insights into how the universe works. We physicists simply noted that the quantity ![]() came up a lot, and we gave it a name
came up a lot, and we gave it a name ![]() . In order to describe how the Universe works, principles often involve multiple definitions. Note that sometimes a principle or definition has an equation, while other times it is just stated in words! This point connects to Physics Goals 1 and 2 for this course.
. In order to describe how the Universe works, principles often involve multiple definitions. Note that sometimes a principle or definition has an equation, while other times it is just stated in words! This point connects to Physics Goals 1 and 2 for this course.
To help acquaint those of you who may not be used to this distinction and to help organize the huge amount of factual information in this particular unit, I will list the principles for this unit. You can quickly see how short this list is.
Principles for This Unit
- “Waves are shy” – Quantum objects like light and electrons exist/propagate as waves. They only really behave in a particle-like manner when they interact/are observed.
- Since quantum objects exhibit both wave and particle properties, we need to be able to move back and forth between the two pictures – As you can see in the table below, both waves and particles have two independent properties. The goal is to move between them.
Wave Properties Particle Properties Amplitude 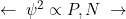
Probability of being at a location / Number of particles Wavelength 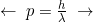
Momentum - A confined wave must “fit in the box” – Thus, we must have an integer number of half-waves. For a nice symmetrical box, or box-like molecule, the wave will evenly fit in the box
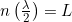 . However, even in situations such as atoms where the electron is more strongly attracted to the nucleus, we will have an integer number of half waves.
. However, even in situations such as atoms where the electron is more strongly attracted to the nucleus, we will have an integer number of half waves. - Energy must be conserved
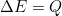
Other Basic Properties You Should Know
- The SI prefixes from nano- (n) to Giga- (G)
- Light in a vacuum always travels at the speed of light
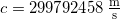
- The
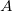 is independent of wavelength
is independent of wavelength 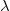
- Free electrons have zero potential energy; all bound electrons, having lower energy than this, have negative potential energy.
 In chemistry, you probably saw the conversion between energy and wavelength for photons done through the equation
In chemistry, you probably saw the conversion between energy and wavelength for photons done through the equation

Instructor’s Note
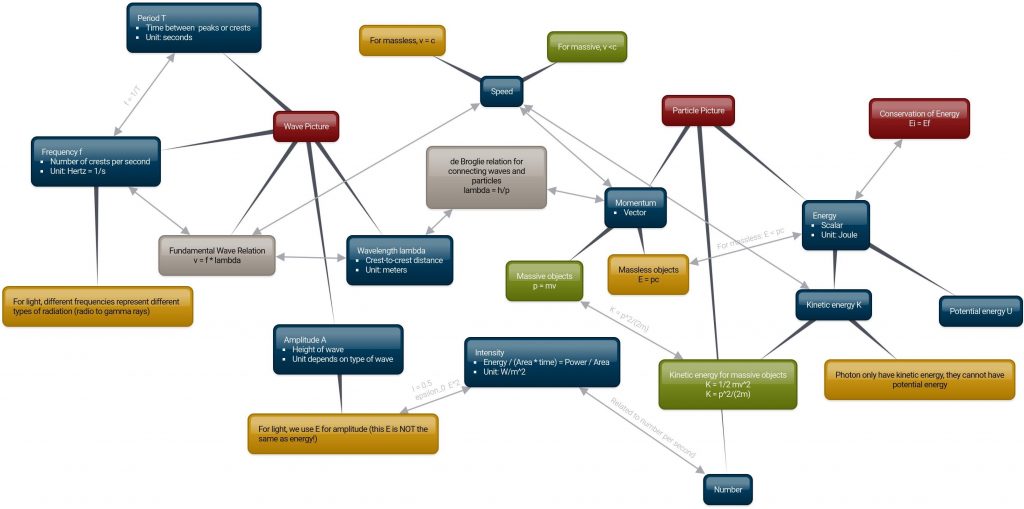
The ideas in this unit can be connected in many different ways. One possible useful way to organize such information is in a “concept map” like the one shown below. The map is also available at this link.
In this map:
- UMass maroon bubbles are big ideas.
- Yellow bubbles apply to massless particles, such as light.
- Green bubbles apply to massive particles, such as electrons.
I recommend printing a copy for use in class!
A fundamental relationship that describes how the Universe works. These are the fundamental truths of Nature. When writing a principle as an equation, the "=" is translated as "causes." For example, Newton's 2nd Law, F = ma, a force F causes an object m to accelerate (change its speed or direction) a. These principles are where we begin our analyses.
An equation representing a common quantity. This equation does not elucidate a fundamental truth of the Universe, it just defines an idea. For example, velocity = distance / time. There are no fundamental truths here, that is just the definition of velocity.
The size of the wave. For a physical wave like a water wave, this will be the actual height in meters. For a sound wave (a pressure wave in the air) this will be in units of pressure Pa.

