24 Time, Velocity, and Speed
OpenStax and Brokk Toggerson
Summary
- Explain the relationship between instantaneous velocity, average velocity, instantaneous speed, average speed, displacement, and time.
- Determine the direction of velocity from the direction of an object’s motion.
- Calculate velocity and speed given initial position, initial position, final position, and final time.

There is more to motion than distance and displacement. Questions such as, “How long does a foot race take?” and “What was the runner’s speed?” cannot be answered without an understanding of other concepts. In this section we add definitions of time, velocity, and speed to expand our description of motion.
Velocity
Your notion of velocity is probably the same as its scientific definition. You know that if you have a large displacement in a small amount of time you have a large velocity, and that velocity has units of distance divided by time, such as miles per hour or kilometers per hour.
Key Takeaways – Velocity
Velocity is displacement (change in position) divided by the time of travel,
![]() .
.
where ![]() is the velocity in the
is the velocity in the ![]() -direction (we will talk more about different directions later!),
-direction (we will talk more about different directions later!), ![]() is the change in position (or displacement), and
is the change in position (or displacement), and ![]() and
and ![]() are the final and beginning positions at times
are the final and beginning positions at times ![]() and
and ![]() , respectively. If the starting time
, respectively. If the starting time ![]() is taken to be zero, then the velocity is simply
is taken to be zero, then the velocity is simply
Notice that this definition indicates that velocity is a vector because displacement is a vector. It has both magnitude and direction. The SI unit for velocity is meters per second or m/s, but many other units, such as km/h, mi/h (also written as mph), and cm/s, are in common use. Suppose, for example, an airplane passenger took 5 seconds to move −4 m (the negative sign indicates that displacement is toward the back of the plane). His average velocity would be
The minus sign indicates the average velocity is also toward the rear of the plane.
The average velocity of an object does not tell us anything about what happens to it between the starting point and ending point, however. For example, we cannot tell from average velocity whether the airplane passenger stops momentarily or backs up before he goes to the back of the plane. To get more details, we must consider smaller segments of the trip over smaller time intervals.
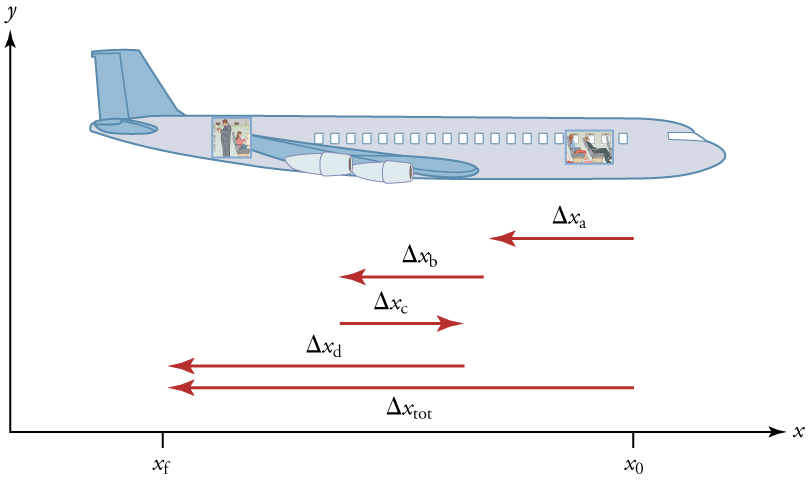
The smaller the time intervals considered in a motion, the more detailed the information. When we carry this process to its logical conclusion, we are left with an infinitesimally small interval. Over such an interval, the average velocity becomes the instantaneous velocity or the velocity at a specific instant. A car’s speedometer, for example, shows the magnitude (but not the direction) of the instantaneous velocity of the car. (Police give tickets based on instantaneous velocity, but when calculating how long it will take to get from one place to another on a road trip, you need to use average velocity.) Instantaneous velocity ![]() is the average velocity at a specific instant in time (or over an infinitesimally small time interval).
is the average velocity at a specific instant in time (or over an infinitesimally small time interval).
Mathematically, finding instantaneous velocity, ![]() , at a precise instant
, at a precise instant ![]() can involve taking a limit, a calculus operation beyond the scope of this text. However, under many circumstances, we can find precise values for instantaneous velocity without calculus.
can involve taking a limit, a calculus operation beyond the scope of this text. However, under many circumstances, we can find precise values for instantaneous velocity without calculus.
Direction of Velocity
One point touched upon above, but not fully expressed concerns the direction of velocity. We see that velocity has a direction. In one dimension, this direction can be expressed with a simple positive or negative sign, but it will be more complex if the motion is in two or three dimensions. Is there a shortcut for figuring out the directions? Yes!
Speed
In everyday language, most people use the terms “speed” and “velocity” interchangeably. In physics, however, they do not have the same meaning and they are distinct concepts. One major difference is that speed has no direction. Thus speed is a scalar. Just as we need to distinguish between instantaneous velocity and average velocity, we also need to distinguish between instantaneous speed and average speed.
Instantaneous speed is the magnitude of instantaneous velocity. For example, suppose the airplane passenger at one instant had an instantaneous velocity of −3.0 m/s (the minus meaning toward the rear of the plane). At that same time his instantaneous speed was 3.0 m/s. Or suppose that at one time during a shopping trip your instantaneous velocity is 40 km/h due north. Your instantaneous speed at that instant would be 40 km/h—the same magnitude but without a direction. A
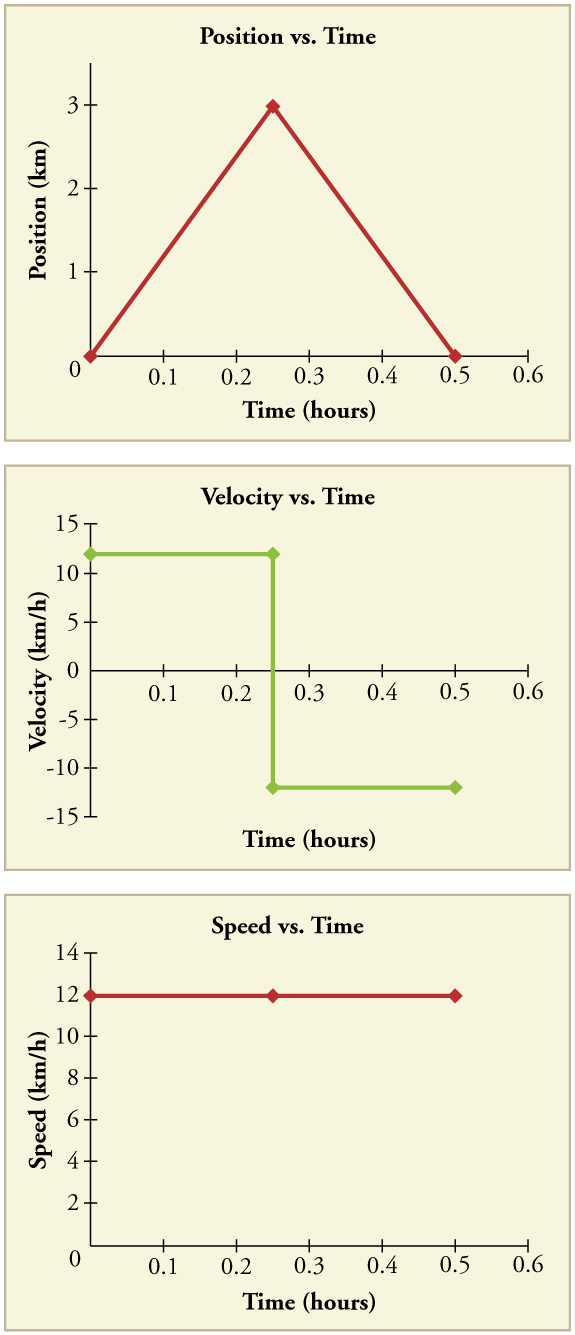
Another way of visualizing the motion of an object is to use a graph. A plot of position or of velocity as a function of time can be very useful. For example, for this trip to the store, the position, velocity, and speed-vs.-time graphs are displayed in Figure 4. (Note that these graphs depict a very simplified model of the trip. We are assuming that speed is constant during the trip, which is unrealistic given that we’ll probably stop at the store. But for simplicity’s sake, we will model it with no stops or changes in speed. We are also assuming that the route between the store and the house is a perfectly straight line.)
Touchstone Values of Velocity
If you have spent much time driving, you probably have a good sense of speeds between about 10 and 70 miles per hour. But what are these in meters per second? What do we mean when we say that something is moving at 10 m/s? To get a better sense of what these values really mean, below is a table of some reference points for velocity that we expect you to have memorized:
| Quantity | Typical Approximate Speeds |
| An amoeba | |
| 1 mile per hour | |
| 1 kilometer per hour | |
| Walking speed | |
| Bicycling speed | |
| Fastest 100m running pace | |
| Highway speeds (60 mi/hr = 100 kph) | |
| Jet airplane | |
| Speed of sound | |
| Speed of light |
Section Summary
- Time is measured in terms of change, and its SI unit is the second (s). Elapsed time for an event is
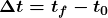
where
 is the final time and
is the final time and  is the initial time. The initial time is often taken to be zero, as if measured with a stopwatch; the elapsed time is then just
is the initial time. The initial time is often taken to be zero, as if measured with a stopwatch; the elapsed time is then just 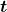 .
. - Average velocity
 is defined as displacement divided by the travel time. In symbols, average velocity is
is defined as displacement divided by the travel time. In symbols, average velocity is
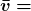
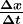

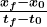 .
. - The SI unit for velocity is m/s.
- Velocity is a vector and thus has a direction.
- Instantaneous velocity
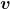 is the velocity at a specific instant or the average velocity for an infinitesimal interval.
is the velocity at a specific instant or the average velocity for an infinitesimal interval. - Instantaneous speed is the magnitude of the instantaneous velocity.
- Instantaneous speed is a scalar quantity, as it has no direction specified.
Homework
9. Touchstone values of speed.
10. Direction of velocity for cars moving around a circle.
11. Speeds of cars on a coordinate system.
12. Driving from the university home.
13. Highway velocities using the kilometer markers.
15. Velocity of a cyclist.

