23 Displacement

OpenStax

If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a white board or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved, or has been displaced.

Key Takeaways – Displacement

Displacement is the change in position of an object:

\boldsymbol{\Delta{x}=x_f-x_0}

where\boldsymbol{\Delta{x}}is displacement,\boldsymbol{x_f}is the final position, and\boldsymbol{x_0}is the initial position.

Since displacement has both a size (how far you moved) and a direction (the direction in which you moved) it is called a quantity: we need to specify both to get a full picture.

 

In this text the upper case Greek letter\boldsymbol{\Delta} (delta) always means “change in” whatever quantity follows it; thus, \boldsymbol{\Delta{x}} means change in position. Always solve for displacement by subtracting initial position \boldsymbol{x_0}from final\boldsymbol{x_f}.

Note that the SI unit for displacement is the meter (m), but sometimes kilometers, miles, feet, and other units of length are used. Keep in mind that when units other than the meter are used in a problem, you may need to convert them into meters to complete the calculation.

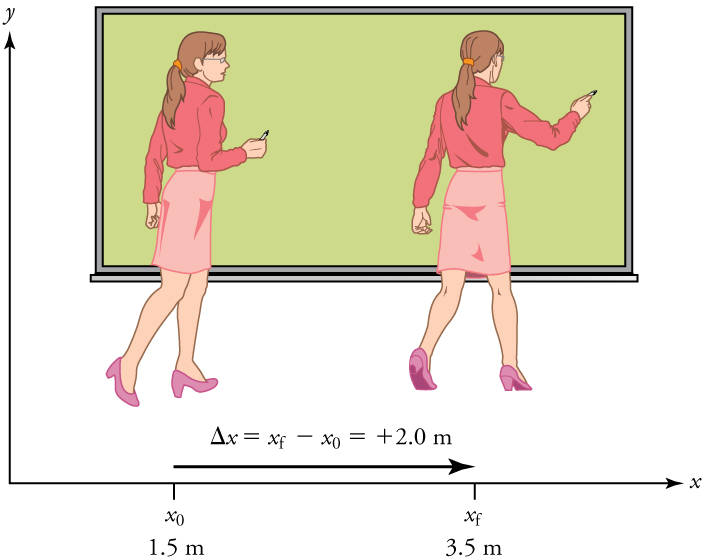
The initial and final position of a professor as she moves to the right while writing on a whiteboard. Her initial position is 1 point 5 meters. Her final position is 3 point 5 meters. Her displacement is given by the equation delta x equals x sub f minus x sub 0 equals 2 point 0 meters.
Figure 2. A professor paces left and right while lecturing. Her position relative to Earth is given by x. The +2.0 m displacement of the professor relative to Earth is represented by an arrow pointing to the right.
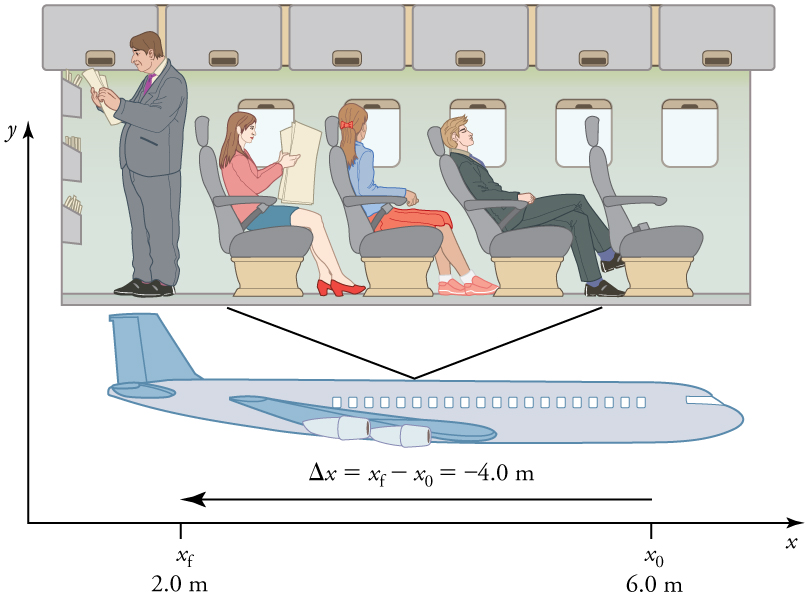
View of an airplane with an inset of the passengers sitting inside. A passenger has just moved from his seat and is now standing in the back. His initial position was 6 point 0 meters. His final position is 2 point 0 meters. His displacement is given by the equation delta x equals x sub f minus x sub 0 equals 4 point zero meters.
Figure 3. A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by x. The -4.0-m displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far) in Figure 2.

 

Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction). The professor’s initial position is \boldsymbol{x_0=1.5\textbf{ m}} and her final position is \boldsymbol{x_f=3.5\textbf{ m}}. Thus her displacement is

\boldsymbol{\Delta{x}=x_f-x_0=3.5\textbf{ m}-1.5\textbf{ m} =+2.0\textbf{ m}}.

In this coordinate system, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger’s initial position is\boldsymbol{x_0=6.0\textbf{ m}}and his final position is\boldsymbol{x_f=2.0\textbf{ m}}, so his displacement is

\boldsymbol{\Delta{x}=x_f-x_0=2.0\textbf{ m}-6.0\textbf{ m}=-4.0\textbf{ m}}.

His displacement is negative because his motion is toward the rear of the plane, or in the negative x direction in our coordinate system.

Quantities which have both a magnitude (size) and a direction, such as displacement, are called .

 Section Summary

  • Kinematics is the study of motion without considering its causes. In this chapter, it is limited to motion along a straight line, called one-dimensional motion.
  • Displacement is the change in position of an object.
  • In symbols, displacement\boldsymbol{\Delta{x}}is defined to be

\boldsymbol{\Delta{x} =x_f -x_0}

where\boldsymbol{x_0}is the initial position and\boldsymbol{x_f}is the final position. In this text, the Greek letter\boldsymbol{\Delta}(delta) always means “change in” what ever quantity follows it. The SI unit for displacement is the meter (m). Displacement has a direction as well as a magnitude.

  • When you start a problem, assign which direction will be positive.
  • Distance is the magnitude of displacement between two positions.

License

Icon for the Creative Commons Attribution 4.0 International License

Displacement by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book