17 Potential Energy
Brokk Toggerson
Gravitational Potential Energy
Learning Objectives
By the end of this section, you should be able to..
- Define potential energy.
- Recall the importance of a system to potential energy.
- List the properties on which gravitational potential energy depends.
Which is Most Important for Gravitational Potential Energy: Mass, Height, or the Planet’s Gravity?
In the video above, we saw that gravitational potential energy depends on three different quantities:
- The mass of the object in question.
- The height at which it exists.
- The strength of gravity on the relevant planet.
However, which of these factors is the most important? We saw, for example, that in kinetic energy speed was more important than mass. What about in the case of gravitational potential energy? Experiments show that these three factors all contribute equally: mass, height, and gravitational strength are all of equal importance to the gravitational potential energy of an object-planet system.
Example: Comparing Gravitational Potential Energy on the Earth and the Moon
Problem:
Which system of block and Earth has more gravitational potential energy:
- A 5 kg block 1m above the surface of the Earth
- A 10kg block 1m above the surface of the Moon (the gravity on the Moon is 1/6 that of Earth).
Solution:
The block near the surface of the Earth will have more potential energy. While the block on the Moon is twice as heavy, the gravity on the Moon is 1/6 that of Earth. The doubling of mass does not make up for the factor of 6 difference in the gravity.
Mass, gravity, and height all matter equally to gravitational potential energy.
Example: Changes in Gravitational Potential Energy
Problem:
A rocket, initially 1m above the ground, goes up an additional 100m. In the process, it loses a lot of mass due to the burning of fuel. In fact, at the peak of its flight, 100m above the ground, it is only 1% of its original mass.
How much has the gravitational potential energy of the rocket-Earth system changed?
Solution:
The gravitational potential energy hasn’t changed! The height has increased by a factor of 100, causing the gravitational potential energy to increase. However, the mass has gone down by the same factor of 100, causing the gravitational potential energy to decrease. Since height and mass are equally important, this increase and decrease cancel each other out yielding no change in gravitational potential energy.
Key Takeaways
- Potential energy is the capability to do work due to the relative positions of objects within a system.
- “It takes two to tango” – you need a system of at least two objects for potential energy to be present.
- Gravitational potential energy is the capacity to do work arising from the position of an object near another.
- The gravitational potential energy depends on three things equally:
- The mass of the object.
- The height.
- The strength of the gravity on planet where the object is located.
Potential Energy of Springs (Elastic Potential Energy)
Learning Objectives
By the end of this section, you should be able to…
- List a few different physical systems which can be modeled by a spring.
- Define the system under which the potential energy of a spring makes sense as a concept.
- List the properties on which the potential energy of a spring depends and rank the importance.
Which is Most Important for Elastic Potential Energy?
In the video above, we saw that elastic potential energy depends on two things:
- The amount the spring is either stretched or compressed. It doesn’t matter if the spring is stretched or compressed, the change in potential energy is the same.
- The stiffness of the spring (the so-called spring constant) which is different for each spring and usually must be measured as it cannot generally be determined from more underlying principles.
Which of these is more important? Experimentation shows that the amount of compression/stretch is more important than the stiffness of the spring just like how for kinetic energy speed is more important than mass.
Example: Compression vs. Stretching
Problem:
Consider two identical springs. One is stretched 4 cm. The other is compressed 4 cm. Which has more potential energy?
Solution:
The two springs have the same potential energy. They have the same stiffness (spring constant) on account of being identical and they are both deformed the same amount, 4cm. The only difference is that one is compressed and the other is stretched. However, as we saw in the video, the amount of potential energy does not depend on if the spring is stretched or compressed, only the amount by which it is deformed.
Example: : Comparing Two Springs
Problem:
Imagine the two springs from the video:
- The yellow plastic spring.
- The metal spring.
Now, assume that the metal spring is twice as stiff as the plastic one. If the plastic one is stretched twice as far as the metal one, which will have the most potential energy?
Solution:
The plastic spring will have more potential energy. While the metal spring is stiffer, the plastic spring has been stretched further. As mentioned above, the amount of deformation (stretching or compressing) has more impact than the stiffness of the spring. Thus the factor of 2 in stretch matters more than the factor of 2 in stiffness.
Key Takeaways
- The relevant system for the potential energy of a spring is the spring and whatever is pushing/pulling against it.
- The potential energy of a spring depends on:
- The stiffness of the spring in question – this varies from spring to spring and must be measured.
- How far the spring is deformed (stretched or compressed).
- It doesn’t matter if the spring is stretched or compressed, the result is the same.
- The amount of deformation of the spring is more important than the stiffness.
Where is Potential Energy Zero? (And Does It Matter?)
Learning Objectives
By the end of this section, you should be able to…
- Describe the freedom associated with a potential energy of zero.
- Recall that only the change in potential energy is a physically relevant quantity.
- Recall, and explain why, negative potential energies are possible.
In the above two types of potential energy, there seem to be logical configurations of the system with zero potential energy:
- A ball sitting on the ground would seem to have zero gravitational potential energy.
- An un-deformed spring would seem to have zero elastic potential energy.
However, as is usual in science, we need to question these assumptions! Do these “obvious” configurations that “seem to clearly” not have potential energy actually not have any potential energy? Are there other ways to think about these configurations which provide some additional insight?
The Ball Sitting on the Ground
The Problem
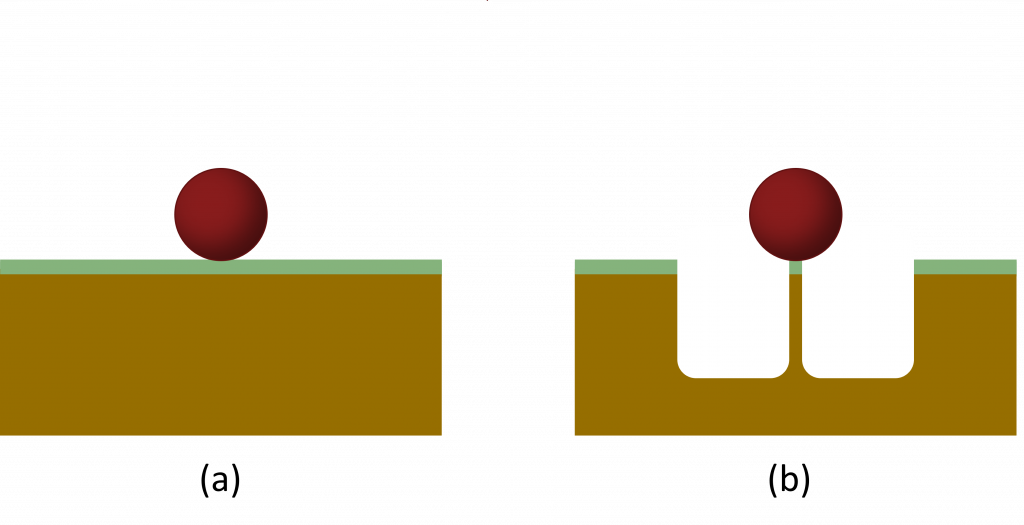
Imagine a ball sitting on the ground as in the left image below. Following the discussion about gravitational potential energy above, we would expect this ball-Earth system to have zero potential energy. The height of the ball is zero after all!
However, now imagine that we dug a hole under the ball using a pole or something to keep the ball where it is, similar to that shown in the right picture. The ball has not moved, but it seems to now have a height as it is some distance above the floor of the hole! How do we reconcile this? The ball didn’t move, we just changed the configuration around it, and yet it went from a situation with seemingly zero height (and therefore no gravitational potential energy) to a state where it does have a height/potential energy.
The Solution
The simplest solution to this problem is to say that since the height of the ball did not change, neither did its potential energy. The height and the potential energy of the ball are zero both before and after the hole is dug. Essentially, we choose the ground level in (a) in the picture above to be a height of zero. Thus, we also choose the gravitational potential energy to be zero at ground level.
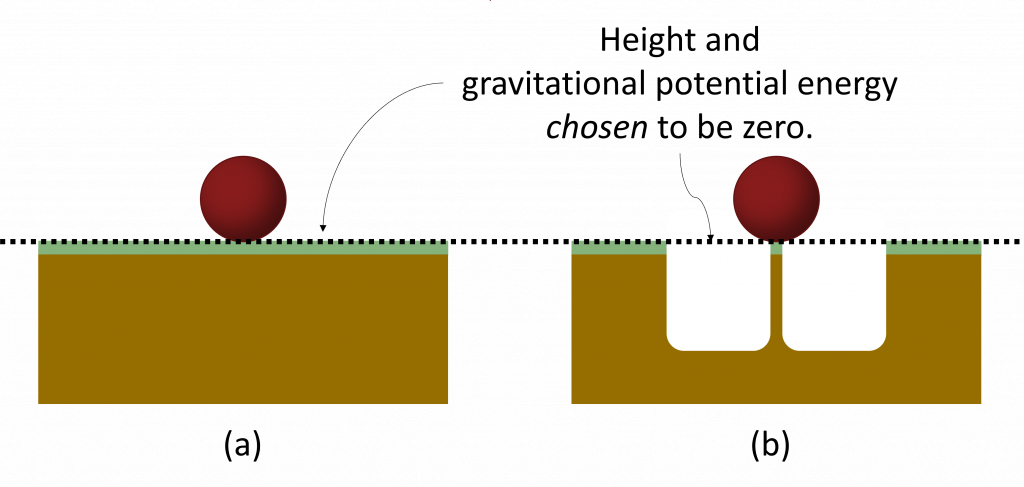
Consequences – What if the ball in (b) falls off its post? What will the potential energy be then?
If the ball falls off its post, as shown below, then it will fall below the height where we chose height and potential energy to be zero. In this case, the potential energy of the ball-Earth system will be less than zero: i.e., the potential energy will be negative. This may seem odd at first, the concept of negative potential energy, but I would ask you to, again, challenge your assumptions and preconceptions. Why can potential energy not be negative? If you think deeply, you will see that there is nothing which forbids a negative potential energy. Thus, we should, in the absence of evidence forbidding it, accept the concept as allowed.
Example: Possible Values of Potential Energy
Problem:
You are standing on the ground. What is the sign (negative, zero, or positive) of the you-Earth system’s gravitational potential energy?
Solution:
Your gravitational potential energy could be any of these: positive, negative or zero; It depends on where we have defined the potential energy to be zero! You might intuitively think that, “if I am on the ground, then, by definition, I could not exert a push or pull by falling. Thus, my potential energy must be zero.” However, this reasoning ignores the possibility of a hole being dug underneath you like in the example above.
- If the ground is chosen to be a height of zero, then, since you are on the ground, and the gravitational potential energy is also zero.
- If the center of the Earth, for example, is chosen to be zero, then you have a height of about 6,378 km. There would also be a positive potential energy associated with that height.
- If, on the other hand, the people on the International Space Station (ISS) were doing the choosing, they might choose their position to be zero height. In this case, your height would be -400 km (yes, that is a negative sign out front!). If your height is negative, then the potential energy of the you-Earth system is negative.
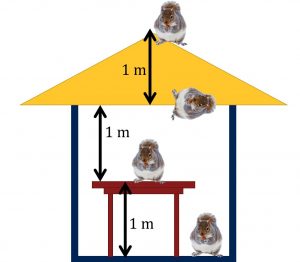
Example: The Potential Energy of a Squirrel
Problem:
Imagine a squirrel sitting on a table that is 
high. Let’s choose the zero of height (and therefore of gravitational potential energy) to be the ceiling, an additional above the table’s surface. With this choice, the potential energy of the gift is 
.
What is the potential energy of the gift-Earth system if the squirrel is:
- Stuck to the ceiling.
- On the roof 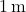above the ceiling.
- On the floor.
Solution:
a. The squirrel is stuck to the ceiling.
In this case, the squirrel has zero height according to our choice. We chose the height to be zero on the ceiling. Thus, the Earth-squirrel system has zero potential energy at this point.
b. The squirrel is on the roof, above the ceiling.
In this case, the squirrel is above the ceiling. Since the zero is defined as the ceiling, the squirrel on the roof has positive height and, therefore, the squirrel-Earth system has positive potential energy. How much? Well, if the Earth-squirrel system has 
of potential energy when the squirrel is below the ceiling then it must have 
when the squirrel is above the ceiling; everything is the same: the mass of the squirrel, the gravity of the planet, and the height. The only thing that has changed is the height which just switched sign (it went from 
to 
).
c. The squirrel is on the floor.
If this case, the squirrel is still below the ceiling and therefore the Earth-squirrel system must have negative potential energy. Since the height is twice the original height, the potential energy should also double to 
.
Chemical Potential Energy and the Choice of Where Potential Energy is Zero
The following video is from https://www.nagwa.com/en/videos/674175783851/. You can also click that link to watch it there with subtitles.
Some Sample Bond Energies[1]
| Single Bonds | Multiple Bonds | ||||||
|---|---|---|---|---|---|---|---|
| H—H |
432
|
N—H |
391
|
I—I |
149
|
C = C |
614
|
| H—F |
565
|
N—N |
160
|
I—Cl |
208
|
C ≡ C |
839
|
| H—Cl |
427
|
N—F |
272
|
I—Br |
175
|
O = O |
495
|
| H—Br |
363
|
N—Cl |
200
|
C = O* |
745
|
||
| H—I |
295
|
N—Br |
243
|
S—H |
347
|
C ≡ O |
1072
|
| N—O |
201
|
S—F |
327
|
N = O |
607
|
||
| C—H |
413
|
O—H |
467
|
S—Cl |
253
|
N = N |
418
|
| C—C |
347
|
O—O |
146
|
S—Br |
218
|
N ≡ N |
941
|
| C—N |
305
|
O—F |
190
|
S—S |
266
|
C ≡ N |
891
|
| C—O |
358
|
O—Cl |
203
|
C = N |
615
|
||
| C—F |
485
|
O—I |
234
|
Si—Si |
340
|
||
| C—Cl |
339
|
Si—H |
393
|
||||
| C—Br |
276
|
F—F |
154
|
Si—C |
360
|
||
| C—I |
240
|
F—Cl |
253
|
Si—O |
452
|
||
| C—S |
259
|
F—Br |
237
|
||||
| Cl—Cl |
239
|
||||||
| Cl—Br |
218
|
||||||
| Br—Br |
193
|
||||||
Example: kJ/mol to eV/molecule
Problem:
As described in the video, chemists usually express the potential energy of bonds as kJ/mol as that is the more useful context for the lab. Physicists, however, are usually interested in single atoms (so we can apply the laws of physics to them).
What is the energy in a single C-C bond?
Solution:
We see that C-C has a bonding energy of 347 kJ/mol from the table above. Let’s convert that to eV/atom:
![\[\left( 347 \, \mathrm{kJ/mol} \right) \times \left( \frac{1 \, \mathrm{mol}}{6.022 \times 10^{23} \, \mathrm{molecules}} \right) \times \left( \frac{1000 \, \mathrm{J}}{\rm kJ} \right) \times \left( \frac{ 1 \, \mathrm{eV}}{1.602 \times 10^{-19} \, \mathrm{J}} \right) = 3.59 \, \mathrm{eV}\]](http://openbooks.library.umass.edu/toggerson-131/wp-content/ql-cache/quicklatex.com-a9aeadd774ed0704150f4febd2c502c8_l3.png "Rendered by QuickLaTeX.com")
This value makes sense from our Energy Touchstone Values which says that covalent bonds are in the eV range (this is why I asked you to memorize them!).
Example: Which Has More Potential Energy
Problem:
Which of these molecules has a higher potential energy, H-H or H-F? Recall that 5 > 0 > -5.
Solution:
The H-H molecule has a higher potential energy. As we see in the table above, the H-H bond requires 432 kJ/mol to break apart while the H-F bond requires 565 kJ/mol. Thus, a mole of H-H has -432 kJ of potential energy. In contrast, a mole of H-F has -565 kJ of potential energy, and -432 > -565.
Key Takeaways
For chemical potential energy:
- The potential energy is due to the relative positions of different atoms within a compound.
- The potential energy is generally considered to be negative:
- Atoms infinitely far apart are generally chosen to have zero potential energy.
- Thus, atoms that are bound must have less energy than that ⇒ negative.
- We often express this as kJ/mol though it can be converted to eV/molecule.
What About the Zero of the Elastic Potential Energy of Springs?
In the case of springs, we mentioned in the video above that the amount of potential energy in a spring depends on how much it is deformed: stretched or compressed. An implication of this is that the potential energy of an undeformed spring should have zero potential energy. However, we have just said that I get to choose where potential energy is zero. How do these two facts agree? The answer is that we could define a relaxed spring to have some potential energy. All deformations would then simply be above and beyond this baseline. The examples below will hopefully illustrate this point.
Example: Adding a Baseline Energy to a Spring
Problem:
Imagine a spring which gains 10 J of energy when it is compressed 10cm.
How much potential energy would this spring have if we stretched it 10cm and choose:
- The relaxed spring to have zero potential energy (the usual choice).
- The relaxed spring to have 2 kJ of potential energy.
Solution:
a. If the relaxed spring has zero potential energy:
In this case we are back to our original discussion of springs: the amount of potential energy is the same for a spring stretched 10cm as it is for a spring compressed 10cm. Thus, the stretched spring has 10 J of energy.
b. If the relaxed spring is chosen to have 2 kJ of potential energy:
In this case, the stretching of the spring adds 10 J of energy just as above. However, this is 10J relative to the relaxed state which we have just chosen to be 2kJ. Thus, the total potential energy in this case would be 10 J + 2 kJ = 2010 J of energy.
Key Takeaways
For springs
- We usually choose the relaxed state of the spring to have zero potential energy.
- This is a choice, however, we could make other choices, where the relaxed state has some positive (or negative!) potential energy. Any energy added by deforming the spring would then add to this baseline.
Homework
- Highest to lowest gravitational potential energy.
- Highest to lowest elastic/spring potential energy.
- Potential energy ranking of molecule bonds.
- Not potential energy.
- Potential energy examples; kinetic energy examples (first part of the question).
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Chemical_Bonding/Fundamentals_of_Chemical_Bonding/Bond_Energies ↵
