A First Example to Understand Tension

Brokk Toggerson

To explore this tension, let’s consider a crate suspended above the ground, held up by a rope.

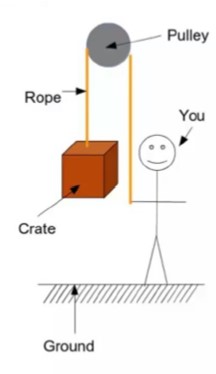
This rope goes over a pulley to you at the other end of the rope. Now, it may be obvious to you the answer to the question “what holds up the stationary crate?”. Well, the rope does, but we want to explore this situation using our physics language.

Let’s consider this situation from a physics perspective. What do we know about the crate? Well, we know that the crate is stationary. The fact that the crate is stationary means that the velocity isn’t changing with respect to time. In other words, there is no net acceleration. By Newton’s second law, no net acceleration implies that there is zero net force, a fact which we can write mathematically like this.

When considering forces in physics, it’s often helpful to draw free body diagrams. Here’s one for this example:

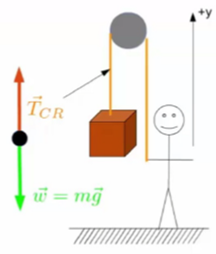
We’ll model the crate as a black dot. What else do we know about this problem? Well, we’ve already determined that the net force has to be zero, which means that there must be some other force pointing in opposition to the force of the weight. By vector addition, if the weight points down and the net force is zero, then this other force must point up. This force is due to the tension within the rope, and so we call it the tension force, and it acts on the crate from the rope. Now let’s apply Newton’s second law to this situation. Remember, the crate is stationary, so there’s no acceleration. We’ll start by just stating Newton’s second law mathematically, the sum of the forces is equal to the mass times the acceleration. The forces in this case include the tension on the crate from the rope and the weight. We’ve already determined that the acceleration must be zero because the crate is stationary. Now, both the tension and the weight force are vectors. Since we’re adding them up, we need to break them into components.

In order to break them into components, we need to establish a coordinate system. We define the y-direction to be positive going up. With this convention, the tension on the crate from the rope is positive, and the weight is negative. Doing the algebra gives us the tension on the crate from the rope is equal to the weight. Would this equality between the tension and the rope and the weight of the box be true if the box were accelerating? No. Why not? Because this equality between the tension in the way only arose because we set the acceleration equal to 0 here in the second step. If that was not true then the tension would not be equal to the weight. What about you on the other end of the rope? How hard do you have to pull down? One property of ropes that we will make extensive use of in this class is that the tension in a rope is the same everywhere. What do I mean by this? Well, we solve for the tension over here where the crate is connected to the rope. By analyzing this part of the system, we can conclude that the tension on the crate from the rope was equal to the weight of the crate.

The fact that the tension must be the same everywhere in the rope means that the tension in the rope where it meets the hand is also equal to the weight. Therefore, the rope is pulling up on my hand with the tension force equal to the weight of the crate which means that if I want everything to stay stationary I have to pull down with a force equal to the weight of the crate to keep everything in place. This should be in conjunction with your everyday experience, where to lift a box using any type of pulley, you’ve got to pull down with at least the weight of the box. The pulley makes it easier because you’re pulling down using your weight to help lift the box as opposed lifting it.

More on Tension

OpenStax

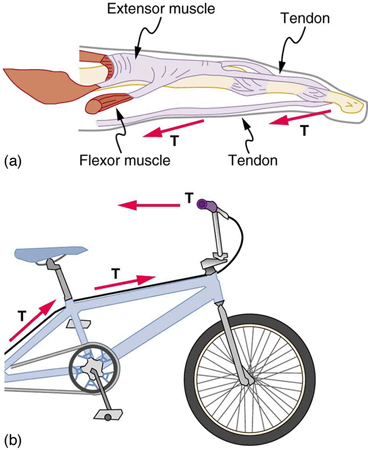
A tension is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable. The word “tension” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons. Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: “You can’t push a rope.” The tension force pulls outward along the two ends of a rope.

Flexible connectors are often used to transmit forces around corners, such as in a hospital traction system, a finger joint, or a bicycle brake cable. If there is no friction, the tension is transmitted undiminished. Only its direction changes, and it is always parallel to the flexible connector. This is illustrated in the figure below (a) and (b).