Dimensions: Space and Time

Brokk Toggerson; OpenStax

22 Dimensions: Space and Time

Brokk Toggerson and OpenStax

Dimensions of Space

The concept of dimensions are used a lot in fiction. Usually they refer to some sort of alternate reality with magical rules or something to that effect. However, what really are dimensions?

A dimension is simply a direction in which you can move. There are three spatial dimensions that we observe in our Universe:

Left/right – Usually called the 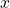$x$ -direction.
Up/down – Usually called the 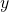$y$ -direction.
Front/back – Usually called the $z$ -direction.

Most of the time in this class, we will be restricted to looking only at motion in two-dimensions: left/right and up/down. However, there are situations, particularly in 132, where you will need to take all three dimensions into account.

If you want to learn more about dimensions, watch this famous video version of the novel Flatland. This is obviously not important for this class, but you might find it interesting!

Time

Every measurement of time involves measuring a change in some physical quantity. It may be a number on a digital clock, a heartbeat, or the position of the Sun in the sky. In physics, the definition of time is simple—time is change, or the interval over which change occurs. It is impossible to know that time has passed unless something changes.

The amount of time or change is calibrated by comparison with a standard. The SI unit for time is the second, abbreviated s. We might, for example, observe that a certain pendulum makes one full swing every 0.75 s. We could then use the pendulum to measure time by counting its swings or, of course, by connecting the pendulum to a clock mechanism that registers time on a dial. This allows us to not only measure the amount of time, but also to determine a sequence of events.

How does time relate to motion? We are usually interested in elapsed time for a particular motion, such as how long it takes an airplane passenger to get from his seat to the back of the plane. To find elapsed time, we note the time at the beginning and end of the motion and subtract the two. For example, a lecture may start at 11:00 A.M. and end at 11:50 A.M., so that the elapsed time would be 50 min. Elapsed time $\boldsymbol{\Delta{t}}$ is the difference between the ending time and beginning time,

$\boldsymbol{\Delta{t}=t_f-t_0}$ ,

where $\boldsymbol{\Delta{t}}$ is the change in time or elapsed time, $\boldsymbol{t_f}$ is the time at the end of the motion, and $\boldsymbol{t_0}$ is the time at the beginning of the motion. (As usual, the delta symbol, $\boldsymbol{\Delta}$ , means the change in the quantity that follows it.)

Life is simpler if the beginning time $\boldsymbol{t_0}$ is taken to be zero, as when we use a stopwatch. If we were using a stopwatch, it would simply read zero at the start of the lecture and 50 min at the end. If $\boldsymbol{t_0=0}$ , then $\boldsymbol{\Delta{t}=t_f\equiv{t}}$ .

In this text, for simplicity’s sake,

motion starts at time equal to zero $\boldsymbol{(t_0=0)}$
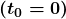
the symbol t is used for elapsed time unless otherwise specified $\boldsymbol{(\Delta{x}=t_f\equiv{t})}$

Time is also often considered a dimension in physics. However, it is a bit different as we can only move in one direction in time: from past to future. Thus, physicists will often say we live in 3+1 dimensions. We get to define where $t =0$ .

Measuring Dimensions – Space

Three people cycling along a canal. The blurred buildings in the background convey a sense of motion of the cyclists. — **Figure 1.** These cyclists in Vietnam can be described by their position relative to buildings and a canal. Their motion can be described by their change in position, or displacement, in the frame of reference. (credit: Suzan Black, Fotopedia).

Position

In order to describe the motion of an object, you must first be able to describe its position—where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of an object as it relates to stationary objects in that reference frame. For example, a rocket launch would be described in terms of the position of the rocket with respect to the Earth as a whole, while a professor’s position could be described in terms of where she is in relation to the nearby white board. (See Figure 2.) In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame. (See Figure 3.)

More on Coordinate Systems

Homework

7. Think about the positions for these cars.

8. How does the positions in different coordinate systems compare?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics 131: What Is Physics? by Brokk Toggerson and OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.