3 Probability, Means, and Standard Deviations
Brokk Toggerson
Let’s begin by giving a little bit more thought to the idea of probability that you’ve explored in some of your readings. The probability of an event is the fraction of time it occurs if the process is repeated an infinite number of times. For a coin, for example, if we flip it fair coin an infinite number of times we expect that one half of them will be heads. Similarly, for a dice, we expect that if we roll it an infinite number of times, one-sixth of the rolls will be a two. Colloquially, the higher the probability, the more likely an outcome is to occur.
If one event does not affect the next, then we say that the events are independent. In this course, we will only be dealing with independent mutually exclusive events. Let’s begin by thinking about an example of interpreting the idea of probability. Say you roll a fair dice. What is the probability that you will roll a six? Well, of course the answer is one out of six. If you were to roll the dice an infinite number of times that, you would observe that one sixth of the rolls would in fact be a six. Now, let’s say you have rolled a dice three times, and the result of each roll has been a six, i.e. you have rolled three sixes in a row. What is the probability that your next roll will also be a six? Well, the answer to this is still 1/6th. Each roll is independent of the previous, so your probability of the next roll being a six is still one out of six, regardless of what has happened in the past. Dice don’t have memory, they don’t remember, so the odds of your next roll being a six are one out of six.
Now with this idea of probability, let’s move on to thinking about how to calculate means of events with differing probabilities. Consider the following set of measurements for the height of the library, as measured, in meters:
88, 87, 88, 90, 90, 88, 85
We know how to calculate the average of a set of numbers; you add up all the numbers and then divide by the number of measurements. In this example, we would add up 88, 87, 88, 90, 90, 88, and 85 and divide by 7, to get an average of 88, but we see in this data set that each result appears to not be equally probable. 88 occurs three-sevenths of the time, and 90 occurs two sevenths of the time. Well, we can deal with this as we just did by adding all the numbers up and counting 88 three times, or we can readjust our definition of average to include the idea of probability:
![]()
[1]
In this new definition, we don’t just add up the events, we add up the probability multiplied by the value. So, we take each value multiplied by the probability, and then add to get the mean. In this example, we say that the probability of 88 is three out of seven, so we multiply 88 and 3/7. The probability of 90 is two out of seven, and so we multiply 88 by 2/7. 87 and 85 both have probabilities of one over seven, and so we multiply 87 and 85 by 1/7. If you churn this out in your calculator, you will see that you get the exact same result of 88. So, clearly these two methods yield the same result, however, the second is more powerful if we don’t know the full data, but, say, only know the probabilities of different outcomes.
Now let’s move on to thinking about calculating standard deviations of events with different probabilities. Here in this table, we have some data
| Value |
Probability |
|---|---|
| 2 | 0.2 |
| 4 | 0.4 |
| 6 | 0.1 |
| 8 | 0.3 |
What is the standard deviation of these data? Well, in our formula for mean, all we did was we change the 1/N to the probability of a given event. You would do the same thing for standard deviation. You do the same thing for standard deviation; instead of multiplying by 1/N out front, you bring it inside the sum, N multiplied by the probability. So now, this equation says take each event, subtract the mean, square it, multiply by the probability, and add them all up, and that will give you the standard deviation squared. Let’s test this formula using these data. We would begin by calculating the mean itself, because the mean is an element of calculating the standard deviation. So, to calculate the mean, we say the mean is the sum of the probability of an event multiplied by the value. In this case, let’s carry out this calculation for these data.
![]()
Evaluating this expression gives us a mean of 5.
So, now that we have a mean, we can proceed to calculating the standard deviation. The way I’m going to do this is I’m going to add a column to my table, ![]() minus the average, or
minus the average, or ![]() , for each value.
, for each value.
| Value |
Probability |
|
|---|---|---|
| 2 | 0.2 | -3 |
| 4 | 0.4 | -1 |
| 6 | 0.1 | 1 |
| 8 | 0.3 | 3 |
In our definition of standard deviation, we care about this value squared, so, let’s continue and add yet another column, squaring, which will get rid of the negatives:
| Value |
Probability |
||
|---|---|---|---|
| 2 | 0.2 | -3 | 9 |
| 4 | 0.4 | -1 | 1 |
| 6 | 0.1 | 1 | 1 |
| 8 | 0.3 | 3 | 9 |
Now we want to multiply each value of x minus mu squared by the probability. So, I’m going to add yet another column, probability times ![]() .
.
| Value |
Probability |
|||
|---|---|---|---|---|
| 2 | 0.2 | -3 | 9 | 1.8 |
| 4 | 0.4 | -1 | 1 | 0.4 |
| 6 | 0.1 | 1 | 1 | 0.1 |
| 8 | 0.3 | 3 | 9 | 2.7 |
Adding these numbers up as instructed gets me a standard deviation squared of 5; turns out that for this data set, the standard deviation squared, and the average are the same. That will not generally be true. I get the standard deviation itself by taking the square root of the standard deviation squared, giving me a standard deviation of 2.24.
In Summary
The probability is the frequency something occurs after an infinite number of trials, and colloquially, we say that the
higher the probability, the more likely a given event is to occur. With this idea of probability, we can adjust our definitions of mean
and standard deviation by swapping out the 1/N out front, and instead multiplying inside the sum by the probability of each
occurrence.
- Some folks use
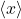 and some use
and some use 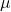 . You need to be comfortable with either. ↵
. You need to be comfortable with either. ↵

