30 Adding Vectors Analytically
OpenStax and Heath Hatch
Learning Objectives
This material is presented both as videos by Heath Hatch and with the relevant OpenStax textbook. Either method is fine. Regardless, by the end of this section, you should be able to:
- Understand the rules of vector addition and subtraction using analytical methods.
- Apply analytical methods to determine the magnitude and direction of a resultant vector.
Adding Vectors Using Analytical Methods
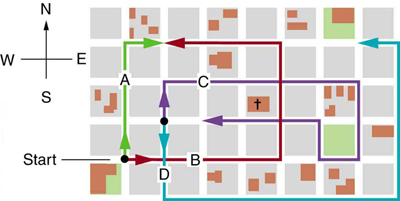
To see how to add vectors using perpendicular components, consider Figure 5, in which the vectors ![]() and
and ![]() are added to produce the resultant
are added to produce the resultant ![]()
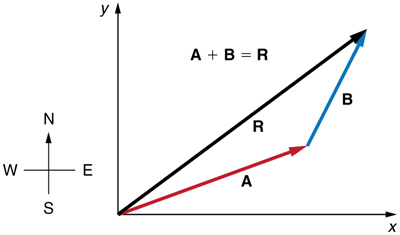
If ![]() and
and ![]() represent two legs of a walk (two displacements), then
represent two legs of a walk (two displacements), then ![]() is the total displacement. The person taking the walk ends up at the tip of
is the total displacement. The person taking the walk ends up at the tip of ![]() There are many ways to arrive at the same point. In particular, the person could have walked first in the x-direction and then in the y-direction. Those paths are the x– and y-components of the resultant,
There are many ways to arrive at the same point. In particular, the person could have walked first in the x-direction and then in the y-direction. Those paths are the x– and y-components of the resultant, ![]() and
and ![]() If we know
If we know ![]() and
and ![]() we can find
we can find ![]() and
and ![]() using the equations
using the equations ![]() and
and ![]() When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.
When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.
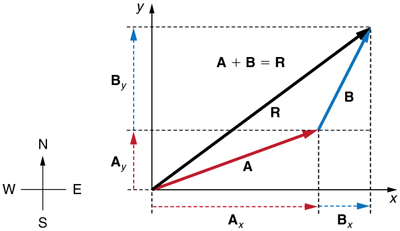
Step 1. Identify the x- and y-axes that will be used in the problem. Then, find the components of each vector to be added along the chosen perpendicular axes. Use the equations ![]() and
and ![]() to find the components. In Figure 6, these components are
to find the components. In Figure 6, these components are ![]() and
and ![]() The angles that vectors
The angles that vectors ![]() and
and ![]() make with the x-axis are
make with the x-axis are ![]() and
and ![]() respectively.
respectively.
Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis. That is, as shown in Figure 7,
and
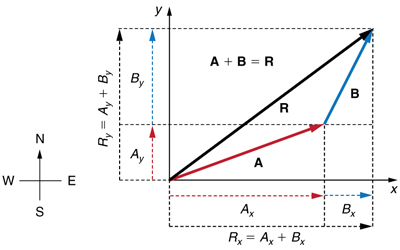
Components along the same axis, say the x-axis, are vectors along the same line and, thus, can be added to one another like ordinary numbers. The same is true for components along the y-axis. (For example, a 9-block eastward walk could be taken in two legs, the first 3 blocks east and the second 6 blocks east, for a total of 9, because they are along the same direction.) So resolving vectors into components along common axes makes it easier to add them. Now that the components of ![]() are known, its magnitude and direction can be found.
are known, its magnitude and direction can be found.
Step 3. To get the magnitude ![]() of the resultant, use the Pythagorean theorem:
of the resultant, use the Pythagorean theorem:
Step 4. To get the direction of the resultant:
The following example illustrates this technique for adding vectors using perpendicular components.
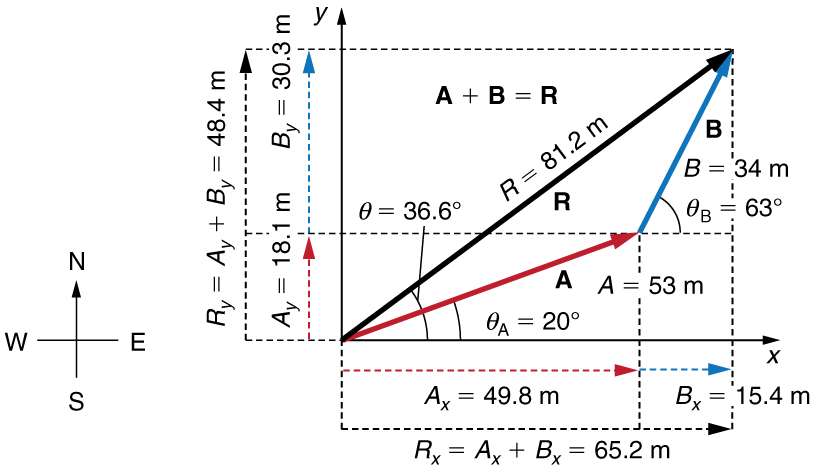
Example 1: Adding Vectors Using Analytical Methods
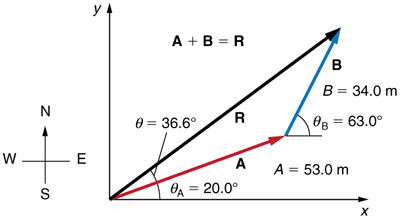
Add the vector ![]() to the vector
to the vector ![]() shown in Figure 8, using perpendicular components along the x– and y-axes. The x– and y-axes are along the east–west and north–south directions, respectively. Vector
shown in Figure 8, using perpendicular components along the x– and y-axes. The x– and y-axes are along the east–west and north–south directions, respectively. Vector ![]() represents the first leg of a walk in which a person walks
represents the first leg of a walk in which a person walks ![]() in a direction
in a direction ![]() north of east. Vector
north of east. Vector ![]() represents the second leg, a displacement of
represents the second leg, a displacement of ![]() a direction
a direction ![]() north of east.
north of east.
Strategy
The components of ![]() and
and ![]() along the x– and y-axes represent walking due east and due north to get to the same ending point. Once found, they are combined to produce the resultant.
along the x– and y-axes represent walking due east and due north to get to the same ending point. Once found, they are combined to produce the resultant.
Solution
Following the method outlined above, we first find the components of ![]() and
and ![]() along the x– and y-axes. Note that
along the x– and y-axes. Note that ![]() and
and ![]() We find the x-components by using
We find the x-components by using ![]() which gives
which gives
and
Similarly, the y-components are found using ![]()
and
The x– and y-components of the resultant are thus
and
Now we can find the magnitude of the resultant by using the Pythagorean theorem:
so that
Finally, we find the direction of the resultant:
Thus,
Discussion
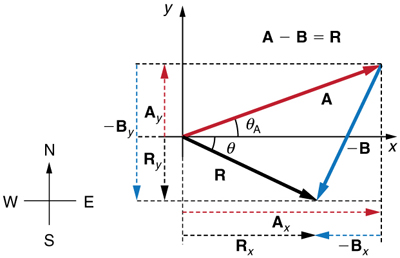
This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.
Subtraction of vectors is accomplished by the addition of a negative vector. That is, ![]() Thus, the method for the subtraction of vectors using perpendicular components is identical to that for addition. The components of
Thus, the method for the subtraction of vectors using perpendicular components is identical to that for addition. The components of ![]() are the negatives of the components of
are the negatives of the components of ![]() The x– and y-components of the resultant
The x– and y-components of the resultant ![]() are thus
are thus
and
and the rest of the method outlined above is identical to that for addition. (See Figure 10.)
Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another. The next module, Chapter 3.4 Projectile Motion, is one of many in which using perpendicular components helps make the picture clear and simplifies the physics.
PHET EXPLORATIONS: VECTOR ADDITION
Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.

Summary
- The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector.
- The steps to add vectors
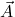 and
and 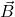 using the analytical method are as follows:
using the analytical method are as follows:
Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations
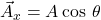
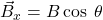
and
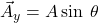
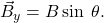
Step 2: Add the horizontal and vertical components of each vector to determine the components
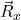 and
and  of the resultant vector,
of the resultant vector, 
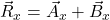
and
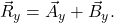
Step 3: Use the Pythagorean theorem to determine the magnitude,
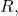 of the resultant vector
of the resultant vector 

Step 4: Use a trigonometric identity to determine the direction,
 of
of 
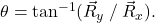
Conceptual Questions
1: Suppose you add two vectors ![]() and
and ![]() What relative direction between them produces the resultant with the greatest magnitude? What is the maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?
What relative direction between them produces the resultant with the greatest magnitude? What is the maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?
2: Give an example of a nonzero vector that has a component of zero.
3: Explain why a vector cannot have a component greater than its own magnitude.
4: If the vectors ![]() and
and ![]() are perpendicular, what is the component of
are perpendicular, what is the component of ![]() along the direction of
along the direction of ![]() What is the component of
What is the component of ![]() along the direction of
along the direction of ![]()
Problems & Exercises
1: Find the following for path C in Figure 12: (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
2: Find the following for path D in Figure 12: (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
3: Solve the following problem using analytical techniques: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements ![]() and
and ![]() as in Figure 14, then this problem asks you to find their sum
as in Figure 14, then this problem asks you to find their sum ![]()
Note that you can also solve this graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.
4: Repeat Exercise 4 using analytical techniques, but reverse the order of the two legs of the walk and show that you get the same final result. (This problem shows that adding them in reverse order gives the same result—that is, ![]() Discuss how taking another path to reach the same point might help to overcome an obstacle blocking you other path.
Discuss how taking another path to reach the same point might help to overcome an obstacle blocking you other path.
5: Do Exercise 4 again using analytical techniques and change the second leg of the walk to ![]() straight south. (This is equivalent to subtracting
straight south. (This is equivalent to subtracting ![]() from
from ![]() —that is, finding
—that is, finding ![]() (b) Repeat again, but now you first walk
(b) Repeat again, but now you first walk ![]() north and then
north and then ![]() east. (This is equivalent to subtract
east. (This is equivalent to subtract ![]() from
from ![]() —that is, to find
—that is, to find ![]() Is that consistent with your result?)
Is that consistent with your result?)
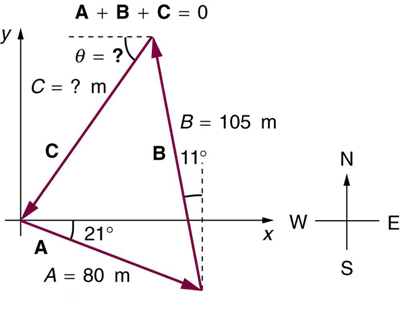
6: A new landowner has a triangular piece of flat land she wishes to fence. Starting at the west corner, she measures the first side to be 80.0 m long and the next to be 105 m. These sides are represented as displacement vectors ![]() from
from ![]() in Figure 15. She then correctly calculates the length and orientation of the third side
in Figure 15. She then correctly calculates the length and orientation of the third side ![]() What is her result?
What is her result?
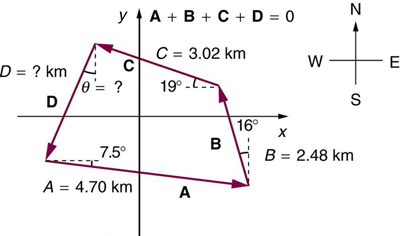
7: A farmer wants to fence off his four-sided plot of flat land. He measures the first three sides, shown as ![]() and
and ![]() in Figure 16, and then correctly calculates the length and orientation of the fourth side
in Figure 16, and then correctly calculates the length and orientation of the fourth side ![]()
What is his result?
8: In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines: ![]() north of west; then
north of west; then ![]() south of east; then
south of east; then ![]() south of west; then
south of west; then ![]() straight east; then
straight east; then ![]() east of north; then
east of north; then ![]() south of west; and finally
south of west; and finally ![]() north of east. What is his final position relative to the island?
north of east. What is his final position relative to the island?
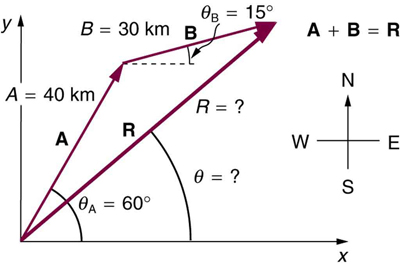
9: Suppose a pilot flies ![]() in a direction
in a direction ![]() north of east and then flies
north of east and then flies ![]() in a direction
in a direction ![]() north of east as shown in Figure 17. Find her total distance
north of east as shown in Figure 17. Find her total distance ![]() from the starting point and the direction
from the starting point and the direction ![]() of the straight-line path to the final position. Discuss qualitatively how this flight would be altered by a wind from the north and how the effect of the wind would depend on both wind speed and the speed of the plane relative to the air mass.
of the straight-line path to the final position. Discuss qualitatively how this flight would be altered by a wind from the north and how the effect of the wind would depend on both wind speed and the speed of the plane relative to the air mass.
Glossary
- analytical method
- the method of determining the magnitude and direction of a resultant vector using the Pythagorean theorem and trigonometric identities
Solutions
Problems & Exercises
1:
(a) 1.56 km
(b) 120 m east
4:
30.8 m, 35.8 west of north
5:
(a) ![]() south of west
south of west
(b) ![]() north of east
north of east
8:
![]() south of east
south of east

