34 Newton’s Second Law of Motion: Concept of a System

OpenStax

Summary

  • Define net force, external force, and system.
  • Understand Newton’s second law of motion.
  • Apply Newton’s second law to determine the weight of an object.

Newton’s second law of motion is closely related to Newton’s first law of motion. It mathematically states the cause and effect relationship between force and changes in motion. Newton’s second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force. Before we can write down Newton’s second law as a simple equation giving the exact relationship of force, mass, and acceleration, we need to sharpen some ideas that have already been mentioned.

First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is an acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes acceleration.

Another question immediately arises. What do we mean by an external force? An intuitive notion of external is correct—an external force acts from outside the system of interest. For example, in Figure 1(a) the system of interest is the wagon plus the child in it. The two forces exerted by the other children are external forces. An internal force acts between elements of the system. Again looking at Figure 1(a), the force the child in the wagon exerts to hang onto the wagon is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law. (The internal forces actually cancel, as we shall see in the next section.) You must define the boundaries of the system before you can determine which forces are external. Sometimes the system is obvious, whereas other times identifying the boundaries of a system is more subtle. The concept of a system is fundamental to many areas of physics, as is the correct application of Newton’s laws. This concept will be revisited many times on our journey through physics.

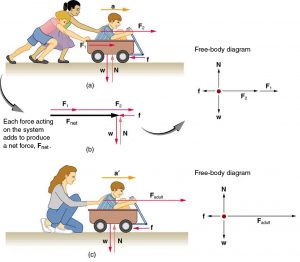
(a) A boy in a wagon is pushed by two girls toward the right. The force on the boy is represented by vector F one toward the right, and the force on the wagon is represented by vector F two in the same direction. Acceleration a is shown by a vector a toward the right and a friction force f is acting in the opposite direction, represented by a vector pointing toward the left. The weight W of the wagon is shown by a vector acting downward, and the normal force acting upward on the wagon is represented by a vector N. A free-body diagram is also shown, with F one and F two represented by arrows in the same direction toward the right and f represented by an arrow toward the left, so the resultant force F net is represented by an arrow toward the right. W is represented by an arrow downward and N is represented by an arrow upward; both the arrows have same length. (b) A boy in a wagon is pushed by a woman with a force F adult, represented by an arrow pointing toward the right. A vector a-prime, represented by an arrow, depicts acceleration toward the right. Friction force, represented by a vector f, acts toward the left. The weight of the wagon W is shown by a vector pointing downward, and the Normal force, represented by a vector N having same length as W, acts upward. A free-body diagram for this situation shows force F represented by an arrow pointing to the right having a large length; a friction force vector represented by an arrow f pointing left has a small length. The weight W is represented by an arrow pointing downward, and the normal force N, is represented by an arrow pointing upward, having the same length as W.
Figure 1. Different forces exerted on the same mass produce different accelerations. (a) Two children push a wagon with a child in it. Arrows representing all external forces are shown. The system of interest is the wagon and its rider. The weight w of the system and the support of the ground N are also shown for completeness and are assumed to cancel. The vector f represents the friction acting on the wagon, and it acts to the left, opposing the motion of the wagon. (b) All of the external forces acting on the system add together to produce a net force, Fnet. The free-body diagram shows all of the forces acting on the system of interest. The dot represents the center of mass of the system. Each force vector extends from this dot. Because there are two forces acting to the right, we draw the vectors collinearly. (c) A larger net external force produces a larger acceleration (a’>a) when an adult pushes the child.

Now, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net (total) external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure 1. In part (a), a smaller force causes a smaller acceleration than the larger force illustrated in part (c). For completeness, the vertical forces are also shown; they are assumed to cancel since there is no acceleration in the vertical direction. The vertical forces are the weight\textbf{w}and the support of the ground\textbf{N},and the horizontal force\textbf{f}represents the force of friction. These will be discussed in more detail in later sections. For now, we will define friction as a force that opposes the motion past each other of objects that are touching. Figure 1(b) shows how vectors representing the external forces add together to produce a net force,\textbf{F}_{\textbf{net}}.

To obtain an equation for Newton’s second law, we first write the relationship of acceleration and net external force as the proportionality

\boldsymbol{\textbf{a}\propto\textbf{F}_{\textbf{net}}},

where the symbol\boldsymbol{\propto}means “proportional to,” and\textbf{F}_{\textbf{net}}is the net external force. (The net external force is the vector sum of all external forces and can be determined graphically, using the head-to-tail method, or analytically, using components as discussed in prior chapters.) This proportionality states what we have said in words—acceleration is directly proportional to the net external force. Once the system of interest is chosen, it is important to identify the external forces and ignore the internal ones. It is a tremendous simplification not to have to consider the numerous internal forces acting between objects within the system, such as muscular forces within the child’s body, let alone the myriad of forces between atoms in the objects, but by doing so, we can easily solve some very complex problems with only minimal error due to our simplification

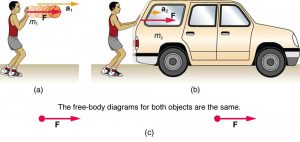
Now, it also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. And indeed, as illustrated in Figure 2, the same net external force applied to a car produces a much smaller acceleration than when applied to a basketball. The proportionality is written as

\boldsymbol{\textbf{a}\:\propto}[latex size=”2″]\boldsymbol{\frac{1}{m}}[/latex]

where\boldsymbol{m}is the mass of the system. Experiments have shown that acceleration is exactly inversely proportional to mass, just as it is exactly linearly proportional to the net external force.

 

(a) A basketball player pushes the ball with the force shown by a vector F toward the right and an acceleration a-one represented by an arrow toward the right. M sub one is the mass of the ball. (b) The same basketball player is pushing a car with the same force, represented by the vector F towards the right, resulting in an acceleration shown by a vector a toward the right. The mass of the car is m sub two. The acceleration in the second case, a sub two, is represented by a shorter arrow than in the first case, a sub one.
Figure 2. The same force exerted on systems of different masses produces different accelerations. (a) A basketball player pushes on a basketball to make a pass. (The effect of gravity on the ball is ignored.) (b) The same player exerts an identical force on a stalled SUV and produces a far smaller acceleration (even if friction is negligible). (c) The free-body diagrams are identical, permitting direct comparison of the two situations. A series of patterns for the free-body diagram will emerge as you do more problems.

It has been found that the acceleration of an object depends only on the net external force and the mass of the object.

Example

Which statement is correct? (a) Net force causes motion. (b) Net force causes change in motion. Explain your answer and give an example.

Solution:

Net force causes change in motion. If I have constant motion, then the net force is in fact zero.

Example

Describe a situation in which the net external force on a system is not zero, yet its speed remains constant.

Solution:

A ball on a string being swung in a circle. The speed is constant, but the velocity vector is constantly changing as the direction changes.

Example

A system can have a nonzero velocity while the net external force on it is zero. Describe such a situation.

Solution:

Any situation where an object has a constant velocity will meet this requirement. For example, a person pushing a block at constant speed across the floor.

Example

A rock is thrown straight up. What is the net external force acting on the rock when it is at the top of its trajectory?

Solution:

At the top of the flight, there is still an acceleration, so there must still be a net force. In this case, the force is the force of gravity.

Example

If the acceleration of a system is zero, are no external forces acting on it?

Solution:

If the acceleration is zero, all we know is that the net force is zero: the total of all forces added vectorally is zero. Thinking again of a person pushing a box across the floor at constant speed, there are two forces acting horizontally: the push forwards and the friction backwards. Since the velocity is constant, we know that the acceleration is zero, and therefore these two forces must be in balance.

Example

If a constant, nonzero force is applied to an object, what can you say about the velocity and acceleration of the object?

Solution:

If there is a net non-zero force, then there must be acceleration, which means that the velocity must change: the object must speed up, slow down, or change direction.

 

Homework

15. Elevator going up a shaft.

16. Woman pushing a box across a floor.

 

License

Icon for the Creative Commons Attribution 4.0 International License

Newton’s Second Law of Motion: Concept of a System by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book