Appendix I: Identify Terms, Coefficients, and Like Terms

OpenStax

Identify Terms, Coefficients, and Like Terms

Algebraic expressions are made up of terms. A term is a constant or the product of a constant and one or more variables. Some examples of terms are 7,y,5{x}^{2},9a,\text{and}\phantom{\rule{0.2em}{0ex}}13xy.

The constant that multiplies the variable(s) in a term is called the coefficient. We can think of the coefficient as the number in front of the variable. The coefficient of the term 3x is 3. When we write x, the coefficient is 1, since x=1\cdot x. The table below gives the coefficients for each of the terms in the left column.

Term Coefficient
7 7
9a 9
y 1
5{x}^{2} 5

An algebraic expression may consist of one or more terms added or subtracted. In this chapter, we will only work with terms that are added together. The table below gives some examples of algebraic expressions with various numbers of terms. Notice that we include the operation before a term with it.

Expression Terms
7 7
y y
x+7 x,7
2x+7y+4 2x,7y,4
3{x}^{2}+4{x}^{2}+5y+3 3{x}^{2},4{x}^{2},5y,3

EXAMPLE 7

Identify each term in the expression 9b+15{x}^{2}+a+6. Then identify the coefficient of each term.

Solution

The expression has four terms. They are 9b,15{x}^{2},a, and 6.

The coefficient of 9b is 9.

The coefficient of 15{x}^{2} is 15.

Remember that if no number is written before a variable, the coefficient is 1. So the coefficient of a is 1.

The coefficient of a constant is the constant, so the coefficient of 6 is 6.

TRY IT 7.1

Identify all terms in the given expression, and their coefficients:

4x+3b+2

Show Answer

The terms are 4x, 3b, and 2. The coefficients are 4, 3, and 2

TRY IT 7.2

Identify all terms in the given expression, and their coefficients:

9a+13{a}^{2}+{a}^{3}

Show Answer

The terms are 9a, 13a2, and a3, The coefficients are 9, 13, and 1

Some terms share common traits. Look at the following terms. Which ones seem to have traits in common?

5x,7,{n}^{2},4,3x,9{n}^{2}

Which of these terms are like terms?

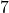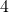  • The terms 7 and 4 are both constant terms.
  • The terms 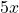5x and 3x are both terms with x.
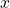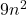  • The terms {n}^{2} and 9{n}^{2} both have {n}^{2}.

Terms are called like terms if they have the same variables and exponents. All constant terms are also like terms. So among the terms 5x,7,{n}^{2},4,3x,9{n}^{2},

7\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}4\phantom{\rule{0.2em}{0ex}}\text{are like terms.}
5x\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}3x\phantom{\rule{0.2em}{0ex}}\text{are like terms.}
{n}^{2}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}9{n}^{2}\phantom{\rule{0.2em}{0ex}}\text{are like terms.}

Like Terms

Terms that are either constants or have the same variables with the same exponents are like terms.

EXAMPLE 8

Identify the like terms:

  1. \phantom{\rule{0.2em}{0ex}}{y}^{3},7{x}^{2},14,23,4{y}^{3},9x,5{x}^{2}
  2. \phantom{\rule{0.2em}{0ex}}4{x}^{2}+2x+5{x}^{2}+6x+40x+8xy
Solution

a. \phantom{\rule{0.2em}{0ex}}{y}^{3},7{x}^{2},14,23,4{y}^{3},9x,5{x}^{2}

Look at the variables and exponents. The expression contains {y}^{3},{x}^{2},x, and constants.

The terms {y}^{3} and 4{y}^{3} are like terms because they both have {y}^{3}.

The terms 7{x}^{2} and 5{x}^{2} are like terms because they both have {x}^{2}.

The terms 14 and 23 are like terms because they are both constants.

The term 9x does not have any like terms in this list since no other terms have the variable x raised to the power of 1.

b. \phantom{\rule{0.2em}{0ex}}4{x}^{2}+2x+5{x}^{2}+6x+40x+8xy

Look at the variables and exponents. The expression contains the terms 4{x}^{2},2x,5{x}^{2},6x,40x,\text{and}\phantom{\rule{0.2em}{0ex}}8xy

The terms 4{x}^{2} and 5{x}^{2} are like terms because they both have {x}^{2}.

The terms 2x,6x,\text{and}\phantom{\rule{0.2em}{0ex}}40x are like terms because they all have x.

The term 8xy has no like terms in the given expression because no other terms contain the two variables xy.

TRY IT 8.1

Identify the like terms in the list or the expression:

9,2{x}^{3},{y}^{2},8{x}^{3},15,9y,11{y}^{2}

Show Answer

9, 15; 2x3 and 8x3, y2, and 11y2

TRY IT 8.2

Identify the like terms in the list or the expression:

4{x}^{3}+8{x}^{2}+19+3{x}^{2}+24+6{x}^{3}

Show Answer

4x3 and 6x3; 8x2 and 3x2; 19 and 24

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics 131: What Is Physics? by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book