Appendix T: Fundamental Relationships from Geometry

OpenStax

Appendix T: Fundamental Relationships from Geometry

OpenStax

This chapter is from 9.4, 9.5, and 9.6 in OpenStax PreAlgebra 2e.

Rectangles

A rectangle has four sides and four right angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length $L$ and the adjacent side as the width, $W$ . See the figure below

A rectangle is shown. Each angle is marked with a square. The top and bottom are labeled L, the sides are labeled W. — A rectangle has four sides, and four right angles. The sides are labeled L for length and W for width.

The perimeter, $P$ of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk

$P = L+W+L+W$

or

$P = 2L + 2W$ .

What about the area of a rectangle? Consider the rug shown below: it is 2 feet long by 3 feet wide, and its area is 6 square feet. Since $A=2 \cdot 3$ , we see that the area, $A$ , is the length, $L$ , times the width, $W$ , so the area of a rectangle is

$A=LW$ .

The area of this rectangular rug is 6 square feet, its length times its width.

Properties of Rectangles

Rectangles have four sides and four right $(90°)$ angles.
The lengths of opposite sides are equal.
The perimeter, 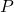$P$ of a rectangle is the sum of twice the length and twice the width: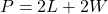 $P = 2L + 2W$
The area, 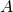$A$ of a rectangle is the length times the width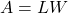 $A = LW$

Triangles

We now know how to find the area of a rectangle. We can use this fact to help us visualize the formula for the area of a triangle. In the rectangle below, we’ve labeled the length $b$ and the width $h$ so it’s area is $bh$ .

A rectangle is shown. The side is labeled h and the bottom is labeled b. The center says A equals bh. — The area of a rectangle is the base, b, times the height, h.

We can divide this rectangle into two triangles as shown below. Triangles that are congruent have identical side lengths and angles, and so their areas are equal. The area of each triangle is one-half the area of the rectangle, or $\frac{1}{2} bh$ . This example helps us see why the formula for the area of a triangle is $A = \frac{1}{2} bh$ .

A rectangle is shown. A diagonal line is drawn from the upper left corner to the bottom right corner. The side of the rectangle is labeled h and the bottom is labeled b. Each triangle says one-half bh. To the right of the rectangle, it says “Area of each triangle,” and shows the equation A equals one-half bh. — A rectangle can be divided into two triangles of equal area. The area of each triangle is one-half the area of the rectangle.

The formula for the area of a triangle is $A = \frac{1}{2} bh$ where $b$ is the base and $h$ is the height.

To find the area of the triangle, you need to know its base and height. The base is the length of one side of the triangle, usually the side at the bottom. The height is the length of the line that connects the base to the opposite vertex, and makes a $90°$ angle with the base. The figure below shows three triangles with the base and height of each marked.

The height h of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a 90° angle with the base.

Triangle Properties

For any triangle $\triangle ABC$ , the sum of the measures of the angles is 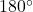$180^\circ$ : $\angle A + \angle B + \angle C = 180^\circ$ .
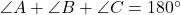The perimeter of a triangle is the sum of the lengths of the sides. $P=a+b+c$
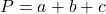
The area of a triangle is one-half the base, b, times the height, h. $A=\frac{1}{2}bh$

A triangle is shown. The vertices are labeled A, B, and C. The sides are labeled a, b, and c. There is a vertical dotted line from vertex B at the top of the triangle to the base of the triangle, meeting the base at a right angle. The dotted line is labeled h.

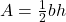
Circles

Properties of Circles

A circle showing the radius and diameter

$r$ is the length of the radius: the distance from the center to the edge of the circle.
$d$ is the length of the diameter: the distance across the circle through the center 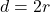$d=2r$
Circumference is the perimeter of a circle. The formula for circumference is $C=2 \pi r$
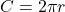
The formula for area of a circle is $A=\pi r^2$

Surface Areas and Volumes

Rectangular Solids

Volume

A cheer-leading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See the figure below). The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.

This is an image of a wooden crate. — This wooden crate is in the shape of a rectangular solid.

Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown below has length $4$ units, width $2$ units, and height $3$ units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.

A rectangular solid is shown. Each layer is composed of 8 cubes, measuring 2 by 4. The top layer is pink. The middle layer is orange. The bottom layer is green. Beside this is an image of the top layer that says “The top layer has 8 cubic units.” The orange layer is shown and says “The middle layer has 8 cubic units.” The green layer is shown and says, “The bottom layer has 8 cubic units.” — Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 4 by 2 by 3 rectangular solid has 24 cubic units.

Altogether there are $24$ cubic units. Notice that $24$ is the $length \times width \times height .$

The top line says V equals L times W times H. Beneath the V is 24, beneath the equal sign is another equal sign, beneath the L is a 4, beneath the W is a 2, beneath the H is a 3.

The volume, $V$ of any rectangular solid is the product of the length, width, and height.

$V = LWH$

We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, $B$ is equal to $length \times width .$

$B = LW$

We can substitute $B$ for $LW$ in the volume formula to get another form of the volume formula.

The top line says V equals red L times red W times H. Below this is V equals red parentheses L times W times H. Below this is V equals red capital B times h.

We now have another version of the volume formula for rectangular solids. Let’s see how this works with the $4 \times 2 \times 3$ rectangular solid we started with An image of a rectangular solid is shown. It is made up of cubes. It is labeled as 2 by 4 by 3. Beside the solid is V equals Bh. Below this is V equals Base times height. Below Base is parentheses 4 times 2. The next line says V equals parentheses 4 times 2 times 3. Below that is V equals 8 times 3, then V equals 24 cubic units.

Surface Area

To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.

$A_{front} = LW$

$A_{front} = 4 \cdot 3$

$A_{front} = 12$

$A_{side} = LW$

$A_{side} = 2 \cdot 3$

$A_{side} = 6$

$A_{top} = LW$

$A_{top} = 4 \cdot 2$

$A_{top} = 8$

Notice for each of the three faces you see, there is an identical opposite face that does not show.

$S=(\mathrm{front}+\mathrm{back})+(\mathrm{left-side}+\mathrm{right-side})+(\mathrm{top}+\mathrm{bottom})$
$S=(2 \cdot \mathrm{front})+(2 \cdot \mathrm{left-side})+(2 \cdot \mathrm{top})$
$S=2 \cdot 12+2 \cdot 6+2 \cdot 8$
$S=24+12+16$
$S=52\, \mathrm{sq. units}$

The surface area $S$ of the rectangular solid shown in below is $52$ square units.

In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its two dimensions, either length and width, length and height, or width and height (see the figure below). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side:

$S=2LH+2LW+2WH$

For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.

Volume and Surface Area of a Rectangular Solid

For a rectangular solid with length $L$ , width $W$ and height $H$

A rectangular solid is shown. The sides are labeled L, W, and H. Beside it is Volume: V equals LWH equals BH. Below that is Surface Area: S equals 2LH plus 2LW plus 2WH.

Spheres

$\begin{matrix} A_{front} = L \times W & A_{side} = L \times W & A_{top} = L \times W \\ A_{front} = 4 \cdot 3 & A_{side} = 2 \cdot 3 & A_{top} = 4 \cdot 2 \\ A_{front} = 12 & A_{side} = 6 & A_{top} = 8 \end{matrix}$
$\begin{matrix} A_{front} = L \times W & A_{side} = L \times W & A_{top} = L \times W \\ A_{front} = 4 \cdot 3 & A_{side} = 2 \cdot 3 & A_{top} = 4 \cdot 2 \\ A_{front} = 12 & A_{side} = 6 & A_{top} = 8 \end{matrix}$

Volume and Surface Area of a Sphere

For a sphere with radius $r :$

An image of a sphere is shown. The radius is labeled r. Beside this is Volume: V equals four-thirds times pi times r cubed. Below that is Surface Area: S equals 4 times pi times r squared.

$\begin{matrix} A_{front} = L \times W & A_{side} = L \times W & A_{top} = L \times W \\ A_{front} = 4 \cdot 3 & A_{side} = 2 \cdot 3 & A_{top} = 4 \cdot 2 \\ A_{front} = 12 & A_{side} = 6 & A_{top} = 8 \end{matrix}$

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics 131: What Is Physics? by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.