25 Acceleration
OpenStax and Brokk Toggerson
Summary
- Define and distinguish instantaneous acceleration, average acceleration, and deceleration.
- Calculate acceleration given initial time, initial velocity, and final velocity.

In everyday conversation, to accelerate means to speed up. The accelerator in a car can in fact cause it to speed up. The greater the acceleration, the greater the change in velocity over a given time. The formal definition of acceleration is consistent with these notions, but more inclusive.
Key Takeaways – Acceleration
Acceleration is the rate at which velocity changes,
![]()
where ![]() is acceleration,
is acceleration, ![]() is velocity, and
is velocity, and ![]() is time. Note that both
is time. Note that both ![]() and
and ![]() have arrows
have arrows ![]() over them which indicates that these quantities have both a magnitude and a direction.
over them which indicates that these quantities have both a magnitude and a direction.
Because acceleration is velocity in m/s divided by time in s, the SI units for acceleration are ![]() meters per second squared or meters per second per second, which literally means by how many meters per second the velocity changes every second.
meters per second squared or meters per second per second, which literally means by how many meters per second the velocity changes every second.
Examples – Units of Acceleration
Problem:
The imperial unit of acceleration is ![]() which is said as either
which is said as either
- feet per second-squared
- feet per second per second
Interpret an acceleration of ![]() .
.
Solution:
An acceleration of ![]() means that the speed increases by
means that the speed increases by ![]() each second. If I start at rest, this means that:
each second. If I start at rest, this means that:
| time [s] | Speed [ft/s] |
| 0 | 0 |
| 1 | 32 |
| 2 | 64 |
| 3 | 96 |
Touchstone Values of Acceleration
It is often useful to have some values two which you can compare your accelerations. Does the answer you get make sense? In order to do this, you need to have some values of acceleration in your head. We expect you to have memorized these values.
| Situation | Acceleration [m/s2] |
| Maximum acceleration of an average gasoline powered car. | 4.5 |
| Maximum acceleration of the Space-X Dragon capsule on launch. | 44 |
| Acceleration at which most untrained humans begin to experience dizziness and fainting. | 49 |
| The maximum acceleration a fit and trained human can endure for any duration without losing consciousness. | 88 |
| Maximum acceleration of a jumping flea | 3200 |
| Typical acceleration of a hit baseball. | 29 460 |
Acceleration as a Vector
Recall that velocity is a vector—it has both magnitude and direction. This means that a change in velocity can be a change in magnitude (or speed), but it can also be a change in direction. For example, if a car turns a corner at constant speed, it is accelerating because its direction is changing. The quicker you turn, the greater the acceleration. So there is an acceleration when velocity changes either in magnitude (an increase or decrease in speed) or in direction, or both.
Keep in mind that although acceleration is in the direction of the change in velocity, it is not always in the direction of motion. When an object slows down, its acceleration is opposite to the direction of its motion.

Negative acceleration, does NOT always imply a reduction in speed: negative acceleration is acceleration in the negative direction in the chosen coordinate system. Negative acceleration may or may not be slowing down and slowing down may or may not be considered negative acceleration. In general, if the acceleration and the velocity have opposite signs, the object is slowing down.
Key Takeaways – Sign of Acceleration
The sign of acceleration is a bit tricky for many students. A negative acceleration does not mean slowing down. To determine if an object is speeding up or slowing down, you need to look at the directions (signs in the 1-D case) of both velocity and acceleration.
- If the two have the same sign: the object is speeding up.
- If the two have opposite signs: the object is slowing down.
| Situation | Sign of |
Sign of |
| Moving in the positive direction and speeding up. | + (Moving in the positive direction.) | + (Must be the same as the sign of v as we are speeding up.) |
| Moving in the positive direction and slowing down. | + (Moving in the positive direction.) | – (Must be opposite the sign of v as we are slowing down.) |
| Moving in the negative direction and speeding up. | – (Moving in the negative direction.) | – (Must be the same as the sign of v as we are speeding up.) |
| Moving in the negative direction and slowing down. | – (Moving in the negative direction.) | + (Must be in the opposite direction of v as we are slowing down.) |
Example 1: A Car
Problem:
Consider the figure below:
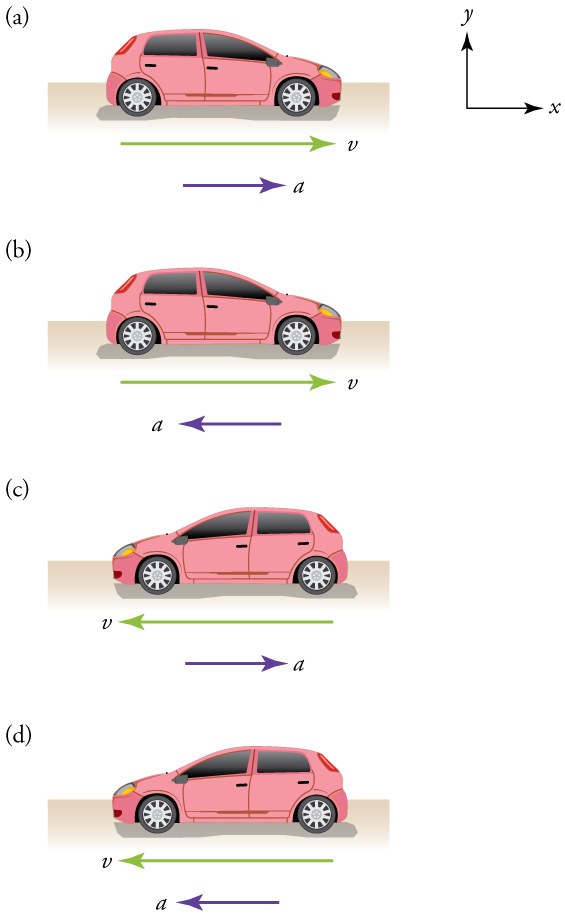
For each sub-figure, is the car speeding up or slowing down?
Solution:
(a) This car is speeding up as it moves toward the right. It therefore has positive acceleration in our coordinate system.
(b) This car is slowing down as it moves toward the right. Therefore, it has negative acceleration in our coordinate system, because its acceleration is toward the left. The car is also slowing down: the direction of its acceleration is opposite to its direction of motion.
(c) This car is moving toward the left, but slowing down over time. Therefore, its acceleration is positive in our coordinate system because it is toward the right. However, the car is slowing down because its acceleration is opposite to its motion.
(d) This car is speeding up as it moves toward the left. It has negative acceleration because it is accelerating toward the left. However, because its acceleration is in the same direction as its motion, it is speeding up.
Example 2: Calculating Acceleration as a Racehorse Leaves the Gate
Problem:
A racehorse coming out of the gate accelerates from rest to a velocity of 15.0 m/s due west in 1.80 s. What is its average acceleration?

Solution:
Strategy
First we draw a sketch and assign a coordinate system to the problem. This is a simple problem, but it always helps to visualize it. Notice that we assign east as positive and west as negative. Thus, in this case, we have negative velocity.
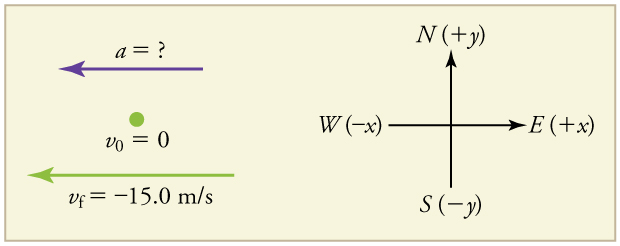
We can solve this problem by identifying ![]() and
and ![]() from the given information and then calculating the average acceleration directly from the equation
from the given information and then calculating the average acceleration directly from the equation ![]()
![]()
![]() .
.
Solution
1. Identify the knowns. ![]() ,
, ![]() (the negative sign indicates direction toward the west),
(the negative sign indicates direction toward the west), ![]() .
.
2. Find the change in velocity. Since the horse is going from zero to ![]() , its change in velocity equals its final velocity:
, its change in velocity equals its final velocity: ![]() .
.
3. Plug in the known values ( ![]() and
and ![]() ) and solve for the unknown
) and solve for the unknown ![]() .
.
Discussion
The negative sign for acceleration indicates that acceleration is toward the west. An acceleration of ![]() due west means that the horse increases its velocity by 8.33 m/s due west each second, that is, 8.33 meters per second per second, which we write as
due west means that the horse increases its velocity by 8.33 m/s due west each second, that is, 8.33 meters per second per second, which we write as ![]() . This is truly an average acceleration, because the ride is not smooth. We shall see later that an acceleration of this magnitude would require the rider to hang on with a force nearly equal to his weight.
. This is truly an average acceleration, because the ride is not smooth. We shall see later that an acceleration of this magnitude would require the rider to hang on with a force nearly equal to his weight.
The next several examples consider the motion of the subway train shown below. In (a) the train moves to the right, and in (b) it moves to the left. The examples are designed to further illustrate aspects of motion and to illustrate some of the reasoning that goes into solving problems.
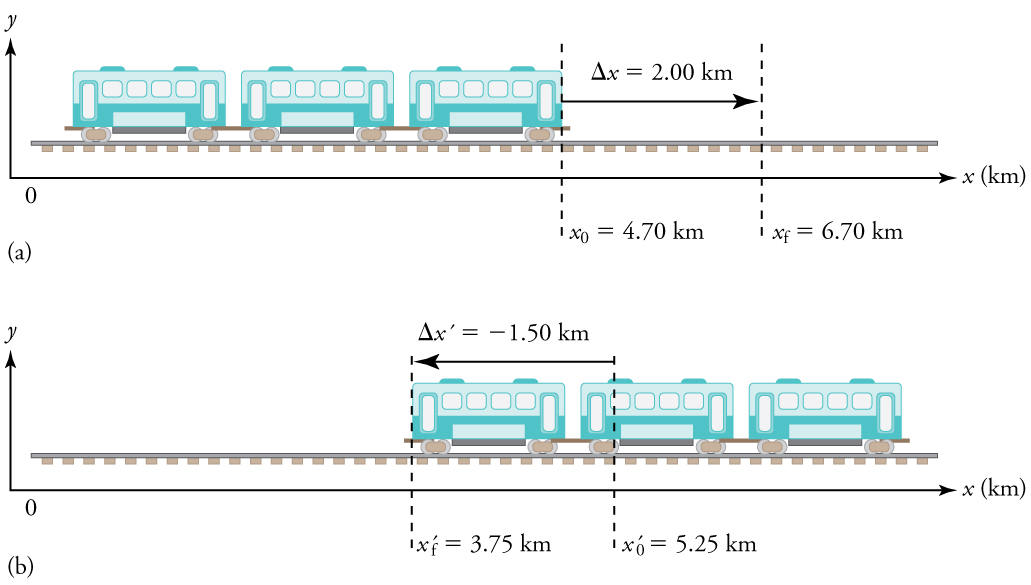
Example 3: Calculating Displacement: A Subway Train
Problem:
What are the magnitude and sign of displacements for the motions of the subway train shown in parts (a) and (b) of the subway figure above?
Strategy
A drawing with a coordinate system is already provided, so we don’t need to make a sketch, but we should analyze it to make sure we understand what it is showing. Pay particular attention to the coordinate system. To find displacement, we use the equation ![]() . This is straightforward since the initial and final positions are given.
. This is straightforward since the initial and final positions are given.
Solution
1. Identify the knowns. In the figure we see that ![]() and
and ![]() for part (a), and
for part (a), and ![]() and
and ![]() for part (b).
for part (b).
2. Solve for displacement in part (a).
3. Solve for displacement in part (b).
Discussion
The direction of the motion in (a) is to the right and therefore its displacement has a positive sign, whereas motion in (b) is to the left and thus has a negative sign.
Example 4: Calculating Acceleration: A Subway Train Speeding Up
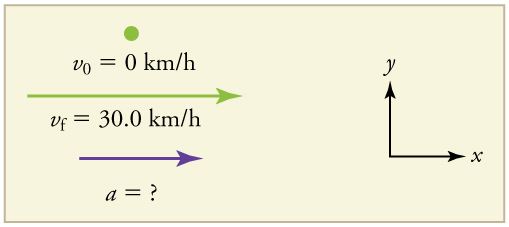
Problem:
Suppose the train in the figure above accelerates from rest to 30.0 km/h in the first 20.0 s of its motion. What is its average acceleration during that time interval?
Solution:
It is worth it at this point to make a simple sketch:
This problem involves three steps. First we must determine the change in velocity, then we must determine the change in time, and finally we use these values to calculate the acceleration.
1. Identify the knowns. ![]() (the trains starts at rest),
(the trains starts at rest), ![]() , and
, and ![]() .
.
2. Calculate ![]() . Since the train starts from rest, its change in velocity is
. Since the train starts from rest, its change in velocity is ![]() , where the plus sign means velocity to the right.
, where the plus sign means velocity to the right.
3. Plug in known values and solve for the unknown, ![]() .
.
![]()
4. Since the units are mixed (we have both hours and seconds for time), we need to convert everything into SI units of meters and seconds. (See Chapter 1.2 Physical Quantities and Units for more guidance.)
![]()
Discussion
The plus sign means that acceleration is to the right. This is reasonable because the train starts from rest and ends up with a velocity to the right (also positive). So acceleration is in the same direction as the change in velocity, as is always the case.
Example 5: Calculate Acceleration: A Subway Train Slowing Down
Problem:
Now suppose that at the end of its trip, the train in Figure 7(a) slows to a stop from a speed of 30.0 km/h in 8.00 s. What is its average acceleration while stopping?
Strategy

In this case, the train is decelerating and its acceleration is negative because it is toward the left. As in the previous example, we must find the change in velocity and the change in time and then solve for acceleration.
Solution
1. Identify the knowns. ![]() ,
, ![]() (the train is stopped, so its velocity is 0), and
(the train is stopped, so its velocity is 0), and ![]() .
.
2. Solve for the change in velocity, ![]() .
.
3. Plug in the knowns, ![]() and
and ![]() , and solve for
, and solve for ![]() .
.
4. Convert the units to meters and seconds.
The minus sign indicates that acceleration is to the left. This sign is reasonable because the train initially has a positive velocity in this problem, and a negative acceleration would oppose the motion. Again, acceleration is in the same direction as the change in velocity, which is negative here. This acceleration can be called a deceleration because it has a direction opposite to the velocity.
PHET EXPLORATIONS: MOVING MAN SIMULATION
Learn about position, velocity, and acceleration graphs. Move the little man back and forth with the mouse and plot his motion. Set the position, velocity, or acceleration and let the simulation move the man for you.
Section Summary
- Acceleration is the rate at which velocity changes. In symbols,
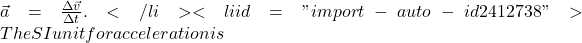 \textbf{ m/s}^2
\textbf{ m/s}^2 \textbf{a}$ is the acceleration at a specific instant in time.
\textbf{a}$ is the acceleration at a specific instant in time. - Slowing down is when acceleration has a direction opposite to that of the velocity.
Homework problems
15. Touchstone values for acceleration.
16. Intercontinental ballistic missiles.
17. Slowing down at the end of a race.
18. Catching a ball.
19. Backing out of a garage.
20. Signs of position velocity and acceleration.
21. Units of position velocity and acceleration.

