Appendix J: Evaluating Algebraic Expressions
OpenStax
Evaluating Algebraic Expressions
In the last section, we simplified expressions using the order of operations. In this section, we’ll evaluate expressions—again following the order of operations.
To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
EXAMPLE 1
Evaluate ![]() when
when
a. To evaluate, substitute ![]() for
for ![]() in the expression, and then simplify.
in the expression, and then simplify.
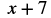 |
|
| Substitute. | 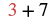 |
| Add. | 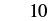 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
b. To evaluate, substitute ![]() for
for ![]() in the expression, and then simplify.
in the expression, and then simplify.
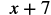 |
|
| Substitute. | 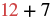 |
| Add. | 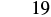 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
Notice that we got different results for parts a) and b) even though we started with the same expression. This is because the values used for ![]() were different. When we evaluate an expression, the value varies depending on the value used for the variable.
were different. When we evaluate an expression, the value varies depending on the value used for the variable.
TRY IT 1.1
Evaluate:
![]()
Show Answer
- 10
- 19
TRY IT 1.2
Evaluate:
![]()
Show Answer
- 4
- 12
EXAMPLE 2
Evaluate ![]()
Remember ![]() means
means ![]() times
times ![]() , so
, so ![]() means
means ![]() times
times ![]() .
.
a. To evaluate the expression when ![]() , we substitute
, we substitute ![]() for
for ![]() , and then simplify.
, and then simplify.
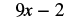 |
|
 |
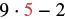 |
| Multiply. | 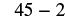 |
| Subtract. |  |
b. To evaluate the expression when ![]() , we substitute
, we substitute ![]() for
for ![]() , and then simplify.
, and then simplify.
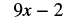 |
|
 |
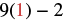 |
| Multiply. | 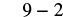 |
| Subtract. |  |
Notice that in part a) that we wrote ![]() and in part b) we wrote
and in part b) we wrote ![]() . Both the dot and the parentheses tell us to multiply.
. Both the dot and the parentheses tell us to multiply.
TRY IT 2.1
Evaluate:
![]()
Show Answer
- 13
- 5
TRY IT 2.2
Evaluate:
![]()
Show Answer
- 8
- 16
EXAMPLE 3
Evaluate ![]() when
when ![]() .
.
We substitute ![]() for
for ![]() , and then simplify the expression.
, and then simplify the expression.
 |
|
 |
 |
| Use the definition of exponent. | 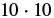 |
| Multiply. | 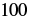 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 3.1
Evaluate:
![]() .
.
Show Answer
64
TRY IT 3.2
Evaluate:
![]() .
.
Show Answer
216
EXAMPLE 4
![]() .
.
In this expression, the variable is an exponent.
 |
|
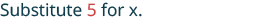 |
 |
| Use the definition of exponent. | 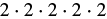 |
| Multiply. |  |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 4.1
Evaluate:
![]() .
.
Show Answer
64
TRY IT 4.2
Evaluate:
![]() .
.
Show Answer
81
EXAMPLE 5
![]() .
.
This expression contains two variables, so we must make two substitutions.
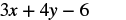 |
|
 |
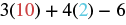 |
| Multiply. | 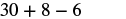 |
| Add and subtract left to right. |  |
When ![]() and
and ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 5.1
Evaluate:
![]()
Show Answer
33
TRY IT 5.2
Evaluate:
![]()
Show Answer
10
EXAMPLE 6
![]() .
.
We need to be careful when an expression has a variable with an exponent. In this expression, ![]() means
means ![]() and is different from the expression
and is different from the expression ![]() , which means
, which means ![]() .
.
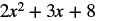 |
|
 |
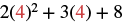 |
| Simplify |
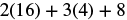 |
| Multiply. | 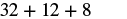 |
| Add. |  |
TRY IT 6.1
Evaluate:
![]() .
.
Show Answer
40
TRY IT 6.2
Evaluate:
![]() .
.
Show Answer
9

