29 Components of Vectors
OpenStax and Heath Hatch
Summary
This material is presented both as videos by Heath Hatch and with the relevant OpenStax textbook. Either method is fine. Regardless, by the end of this section, you should be able to:
- Apply analytical methods to determine vertical and horizontal component vectors.
Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.
Resolving a Vector into Perpendicular Components
Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like ![]() in Figure 1, we may wish to find which two perpendicular vectors,
in Figure 1, we may wish to find which two perpendicular vectors, ![]() and
and ![]() , add to produce it.
, add to produce it.
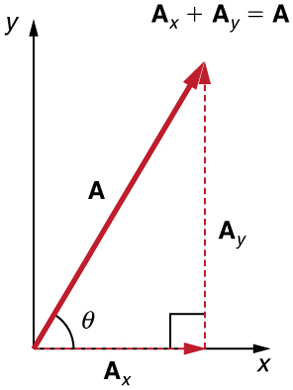
![]() and
and ![]() are defined to be the components of
are defined to be the components of ![]() the x- and y-axes. The three vectors
the x- and y-axes. The three vectors ![]() and
and ![]() form a right triangle:
form a right triangle:
Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if ![]() east,
east, ![]() north, and
north, and ![]() north-east, then it is true that the vectors
north-east, then it is true that the vectors ![]() However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,
However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,
Thus,
If the vector ![]() is known, then its magnitude
is known, then its magnitude ![]() and its angle
and its angle ![]() (its direction) are known. To find
(its direction) are known. To find ![]() and
and ![]() its x- and y-components, we use the following relationships for a right triangle.
its x- and y-components, we use the following relationships for a right triangle.
and
![]A dotted vector A sub x whose magnitude is equal to A cosine theta is drawn from the origin along the x axis. From the head of the vector A sub x another vector A sub y whose magnitude is equal to A sine theta is drawn in the upward direction. Their resultant vector A is drawn from the tail of the vector A sub x to the head of the vector A-y at an angle theta from the x axis. Therefore vector A is the sum of the vectors A sub x and A sub y.](http://openbooks.library.umass.edu/toggerson-131/wp-content/uploads/sites/21/2022/08/Figure_03_03_02a.jpg)
Suppose, for example, that ![]() is the vector representing the total displacement of the person walking in a city considered in Chapter 3.1 Kinematics in Two Dimensions: An Introduction and Chapter 3.2 Vector Addition and Subtraction: Graphical Methods.
is the vector representing the total displacement of the person walking in a city considered in Chapter 3.1 Kinematics in Two Dimensions: An Introduction and Chapter 3.2 Vector Addition and Subtraction: Graphical Methods.
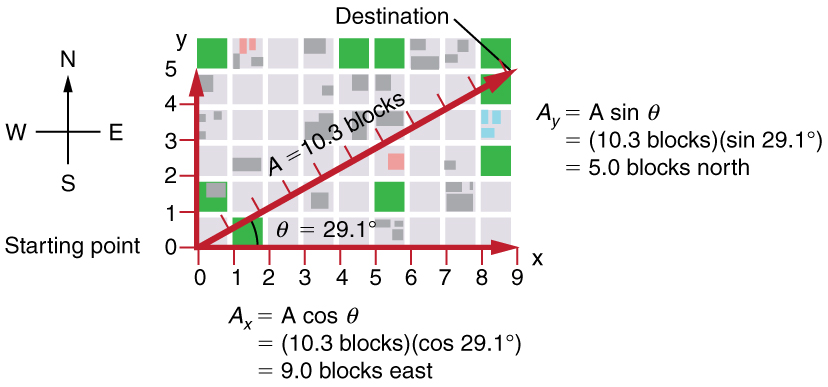
Then ![]() and
and ![]() so that
so that
Calculating a Resultant Vector
If the perpendicular components ![]() and
and ![]() of a vector
of a vector ![]() are known, then
are known, then ![]() can also be found analytically. To find the magnitude
can also be found analytically. To find the magnitude ![]() and direction
and direction ![]() of a vector from its perpendicular components
of a vector from its perpendicular components ![]() and
and ![]() we use the following relationships:
we use the following relationships:
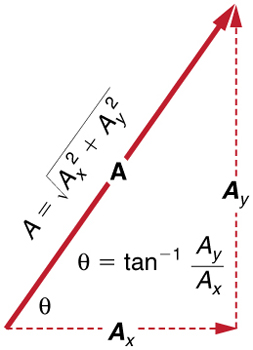
Note that the equation ![]() is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if
is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if ![]() and
and ![]() are 9 and 5 blocks, respectively, then
are 9 and 5 blocks, respectively, then ![]() blocks, again consistent with the example of the person walking in a city. Finally, the direction is
blocks, again consistent with the example of the person walking in a city. Finally, the direction is ![]() as before.
as before.
DETERMINING VECTORS AND VECTOR COMPONENTS WITH ANALYTICAL METHODS
Equations ![]() and
and ![]() are used to find the perpendicular components of a vector—that is, to go from
are used to find the perpendicular components of a vector—that is, to go from ![]() and
and ![]() to
to ![]() and
and ![]() Equations
Equations ![]() and
and ![]() are used to find a vector from its perpendicular components—that is, to go from
are used to find a vector from its perpendicular components—that is, to go from ![]() and
and ![]() to
to ![]() and
and ![]() Both processes are crucial to analytical methods of vector addition and subtraction.
Both processes are crucial to analytical methods of vector addition and subtraction.
Conceptual Questions
1: Give an example of a nonzero vector that has a component of zero.
2: Explain why a vector cannot have a component greater than its own magnitude.
Problems & Exercises
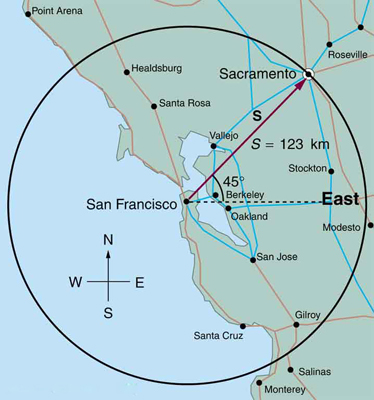
1: Find the north and east components of the displacement from San Francisco to Sacramento shown in Figure 13.
2: You drive ![]() in a straight line in a direction
in a straight line in a direction ![]() east of north. (a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.) (b) Show that you still arrive at the same point if the east and north legs are reversed in order.
east of north. (a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.) (b) Show that you still arrive at the same point if the east and north legs are reversed in order.
3: You fly ![]() in a straight line in still air in the direction
in a straight line in still air in the direction ![]() south of west. (a) Find the distances you would have to fly straight south and then straight west to arrive at the same point. (This determination is equivalent to finding the components of the displacement along the south and west directions.) (b) Find the distances you would have to fly first in a direction
south of west. (a) Find the distances you would have to fly straight south and then straight west to arrive at the same point. (This determination is equivalent to finding the components of the displacement along the south and west directions.) (b) Find the distances you would have to fly first in a direction ![]() south of west and then in a direction
south of west and then in a direction ![]() west of north. These are the components of the displacement along a different set of axes—one rotated
west of north. These are the components of the displacement along a different set of axes—one rotated ![]()
Glossary
- analytical method
- the method of determining the magnitude and direction of a resultant vector using the Pythagorean theorem and trigonometric identities
Solutions
Problems & Exercises
1:
North-component 87.0 km, east-component 87.0 km
2:
30.8 m, 35.8 west of north
3:
(a) 18.4 km south, then 26.2 km west
(b) 31.5 km at ![]() south of west, then 5.56 km at
south of west, then 5.56 km at ![]() west of north
west of north

