7 Combinations
Brokk Toggerson
Learning Objectives
By the end of this chapter, you should be able to…
- Determine the number of ways to arrange
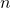items into subsets of 
size.
In order to solve combinations, you need to know how to handle factorials, so make sure you understand the material in the previous section before moving on.
What are the types of questions we are looking to answer with combinations? One example is, say that I have five apples of different varieties, how many different combinations of three apples are there? Another example question would be that there are four teams in an NFL division, how many games are necessary for each team to play every other team in their division? Or another example is, say I have 10 molecules in a box, how many different combinations are there with three molecules on the left-hand side and seven on the right-hand side?
So, what is common amongst these different situations? These problems are looking at a large pool of items and trying to choose a subset where the order of the items is not important. In the first example, I’m trying to choose three apples out of five, it doesn’t matter what order I choose the apples in. In the second example, I’m choosing two teams to play each other out of the four teams in an NFL division. It doesn’t really matter what order the teams play in in this perspective, it just matters how many games do I need. And in the last example, I’m looking to choose three molecules out of ten to be on the right. It doesn’t matter which three, just that there are three.
So, now let’s move on and try and calculate these different combinations. I will explore this in the apple example, wherein I have five apples of different varieties and want to know how many different combinations of three apples are there. The way to calculate the number of combinations is given by the formula
![\[\frac{n!}{(n-r)!r!}\]](https://openbooks.library.umass.edu/toggerson-131/wp-content/ql-cache/quicklatex.com-6fef6f3423271a50f0e096f66f6dfce1_l3.png "Rendered by QuickLaTeX.com")
where is the number of objects in total, in this case five for the five apples, and is the number of objects at your sub group, in this case three, because I want three apples. Plugging in the numbers into this formula, we see
![\[\frac{5!}{(5-3)!3!} = \frac{5!}{(2)!3!} = \frac{120}{2 \cdot 6} = 10\]](https://openbooks.library.umass.edu/toggerson-131/wp-content/ql-cache/quicklatex.com-18f8cf144d95b907137603b7c921cc0a_l3.png "Rendered by QuickLaTeX.com")
There are 10 different combinations of three apples, given the five that I have.
This calculation is called a binomial coefficient, for reasons that are somewhat sophisticated, and this calculation can be represented in several different ways, and you should be familiar with all the different ways of representing this calculation, as different fields tend to use different notation. The calculation can be represented as 
.
