7 Lab Activity 7
Investigating harmonic intervals on musical Instruments: Introduction
As we will discuss further in class, musical instruments can have different tuning schemes, two of which are known as the equal temperament scheme, and the just intonation or just temperament scheme. The purpose of today’s lab investigation is to understand how and why musical instruments are designed to follow one of these tuning methods.
We preface this discussion by noting that the physical, measurable frequency of a pure tone is associated with the psychological perceived pitch of the tone. Likewise, a musical interval that corresponds to the perceived gap between two pitches is physically expressed as a ratio of the associated frequencies. All musical intervals can be expressed as frequency ratios. These frequency ratios can be written as ratios of integers for just temperament intervals, and as multiples of a basic number (the twelfth root of 2) for the equal temperament scheme.
In the ‘equal temperament’ scheme, every semitone increase corresponds to an increase in frequency by a fixed multiplicative factor. What does this mean? Let us begin by explaining what an octave is, what a semitone is, and the musical intervals corresponding to each.
Many musical systems across the world use the idea of an octave – a special interval between musical notes. Notes separated by an octave sound the same to us – they have the same pitch class. In the Western musical system, there are 7 distinct note names in an octave, named for letters of the alphabet. This nomenclature is best illustrated by the C major diatonic scale, which is obtained, for example, by playing, in sequence, just the white keys of a piano keyboard starting with C: (CDEFGABC). Notice that we only need seven letters, because an octave above a C is also a C. To differentiate between octaves, notes are followed by an integer subscript – the higher that subscript, the higher the note. (This is also called the tone-height). The frequency ratio between a note and the same note an octave higher is 1:2, i.e. every time you go from a note to the same note an octave above, the frequency doubles. Thus the frequency of note A2 is 110 Hz, that of A3 is 220 Hz, and that of A4 is 440 Hz, where there is an octave between A2 and A3, and between A3 and A4.
The octave is further divided into 12 semitones, or half tones. In the equal temperament tuning scheme, each half step corresponds to an increase in frequency by a constant multiplicative factor. This fixed multiplicative factor comes from dividing the ratio of 2 for the octave into 12 equal multiplicative factors, i.e. 21/12 = 1.05946, which, multiplied by itself 12 times, gives 2. (The math you need here says that 21/12 *21/12 = 22/12 , or that when you multiply a number raised to one exponent by the same number raised to a different exponent, add the exponents). Note also that 1.05946 is an approximation to 21/12, which is an irrational number.
This scheme allows us to assign frequencies to all the labeled notes. For e.g. f(D) = 293.66 Hz, which means f(D#) = 1.05946*293.6 Hz = 311.12 Hz
In this labeling, D#, or D-sharp, is the note a half step above D. The note a half step below D is D♭ or D-flat. The note a full step above D is given a new name, E. The scale of C-major: CDEFGABC contains no sharps or flats. The entire range of a theoretical piano keyboard is shown in Diagram 1 below (real pianos span 7 ½ octaves, but this shows 9 octaves). The note names, along with their frequencies using the equal temperament tuning scheme, are marked on the diagram. Because of this enormous frequency range, pianos must be tuned using this scheme.
The ‘just intonation’ or ‘just temperament’ tuning scheme, by contrast, exploits the idea of resonant frequencies, or harmonics which are integer multiples of a fundamental. Using a harmonic series, you can find the change in frequency for any musical interval in terms of the ratio between 2 integers. Thus going up by an interval of a perfect fifth corresponds to increasing the starting frequency by a factor of 1.5, which is a ratio of two integers: 3/2.
e.g. A is a perfect fifth above D: f(D) = 293.62 Hz, which means f(A) = (3/2) *293.66 Hz = 440.49 Hz
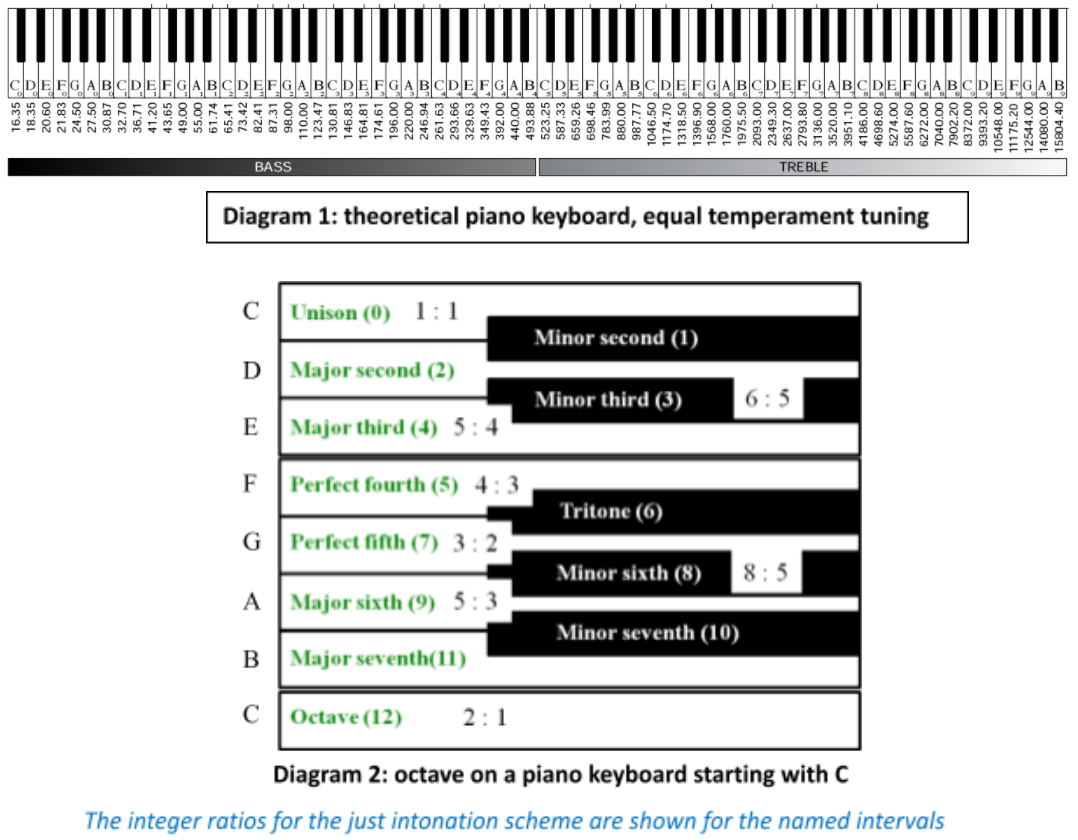
Diagram 2 shows the range of notes corresponding to one full octave on the piano keyboard, starting with C. Going from one key to the next, whether white or black, corresponds to one half step, or semitone. If you use only the white keys in this range, you get the C-major diatonic scale, which consists of a particular sequence of musical intervals: WWHWWWH, where W (whole tone) is two half steps, or a full step, and H is a half step.
The first note on Diagram 2 is C; each successive key carries the name of the musical interval between that key and the first key (C). Thus the interval formed between C and E is a major third. The quantity in parentheses on each key represents the number of half-steps from C to the current note: the (4) written on note E represents 4 half steps up from note C. Finally, the two integers represent the ratio between the frequency of the current key, and the frequency of C, using the just intonation scheme. The label 5:4 on the note E implies that f(E) = 5/4 f(C).
The ‘just intonation’ tuning of instruments usually sounds far more pleasing to musicians, but it becomes harder to transpose music to a different key and preserve the frequency ratios. This is particularly true when the range of octaves the instrument can produce is large, as is the case with a piano.
Today we will study the relationship between the frequencies of two notes of different pitch played on a particular musical instrument. We will pose the question – if the pitch of the two notes that we wish to compare have a well-defined relationship, so that they form a recognizable musical interval such as a third or a fifth, what is the ratio of their frequencies? Pythagoras, who was the first to find the relationship between the length of a string and its harmonics, pointed out that pleasing harmonic intervals will have frequency ratios that can be represented by the ratios of natural numbers (i.e. positive integers). This corresponds to the “just intonation” tuning of instruments.
Lab Activity
Lab Activity
Goal of this lab activity: The question we want to answer by the end of today’s lab is, how is a particular musical instrument tuned? Is it tuned according to the just, or the equal temperament scheme? You will investigate this for a musical instrument of your choice. Make certain that at least one member of your team has a musical instrument you can use.
Equipment needed: A musical Instrument that can play different notes, Laptop with Audacity and microphone OR smartphone with PhyPhox app.
[Exercise 1 below] Describe the musical instrument you are investigating. Name it, give a physical description, and discuss what part of the instrument produces the sound, and what amplifies it. (i.e. describe the primary and secondary oscillators). How is it classified according to the Hornbostel-Sachs scheme?
Two methods for finding note frequency:
- Method 1 (preferred): Open the Phyphox app, and select “Audio Autocorrelation” under the “Acoustics” section. Hit play, then play any one note on the instrument and stop when you have recorded a tone.
- Method 2: Open the program Audacity, and record any one note played on the instrument using the built in microphone. On the left side, you should see a drop down menu for “Audio Track”, which should have waveform selected. Click “Spectrogram”, and a pattern should appear. Find the y-axis (frequency value) of the brightest line – this is the dominant frequency. What is the note corresponding to this frequency? Use Diagram 1 of the piano keyboard provided above.
- Find the range of pitches the instrument can produce (i.e. the lowest and highest notes) both in terms of frequency, and in terms of note names (see Diagram 1). Record bith the frequency and note name for these two notes in your report.
- Next, you will investigate the frequency ratio of intervals. Pick a note on the instrument, record it, find frequency using Method 1 or Method 2. Enter this in the first row of Data Table 1 shown below.
- Now pick six other notes corresponding to specific musical intervals relative to the first, or dominant note. Record them, and use PhyPhox app to find the note names and frequencies, and enter them in columns 3 and 4 of Data Table 1. In column 2, record the musical interval name of each subsequent note relative to the first note of frequency f1. Some required musical intervals have been filled in for you.
- For each musical interval you have measured, use columns 5 and 6 to write down the numerical values of the expected frequency ratios using the equal temperament (column 5) and just intonation (column 6) schemes. For equal temperament, this ratio is equal to (1.05946)n where n = # of semitones in interval. For just intonation, it is the appropriate ratio of integers obtained from Diagram 2.
- Calculate the labeled frequency ratios using your measured frequencies in column 4 relative to the first note of frequency f1 in row 1. Enter the numerical values of these ratios in column 7.
Data Table 1
| # | Interval | Note name | Measured Frequency | Expected freq ratio (equal) | Expected freq ratio (just) | Measured freq ratio |
| 1 | Unison | f1 = | ||||
| 2 | f2 = | f2/f1 = | ||||
| 3 | f3 = | f3/f1 = | ||||
| 4 | Fifth | f4 = | f4/f1 = | |||
| 5 | f5 = | f5/f1 = | ||||
| 6 | f6 = | f6/f1 = | ||||
| 7 | Octave | f7 = | f7/f1 = |
Exercise 1
Describe the musical instrument you are investigating. Name it, give a physical description, and discuss what part of the instrument produces the sound, and what amplifies it. (i.e. describe the primary and secondary oscillators). How is it classified according to the Hornbostel-Sachs scheme?
Exercise 2
Now compare your calculated frequency ratios from your measurements, i.e. column 7 with the expected ratios in columns 5 and 6 for the known musical intervals. Do this for each row. Which scheme do your measured ratios fall closer to?
Exercise 3
Based on your measurements, can you determine whether the musical instrument you used is tuned according to the just or equal temperament schemes? Discuss, and justify your reasoning. Does this make sense in the context of the type of instrument this is?
