2 Collecting Data
In this lab you will compare measurements of acceleration from the accelerometer and wheel sensors to determine which one is the most accurate.
Learning Goals:
- Collect data from multiple sources.
- Compare data using mean, standard deviation, and standard error of the mean.
Part 1: Collecting Acceleration Data
- Make sure the accelerometer is calibrated to your computer.
- From the Sensor list, choose the Accelerometer and Wheel Acceleration sensors. You will only need to look at the y-axis so you can uncheck “Ax” and “Az” on the Accelerometer sensor.
- Place the iOLab device wheel side down on a flat surface. Then start Recording and apply a quick push to the Force sensor. The force should be strong enough that the iOLab can roll for a couple of seconds afterward.
- Be sure to save your data and label it so it is easy to find later.
- Zoom in so you can see the data in more detail. You can see below some sample data of what before and after zooming should look like.


-
- Determine the part of the graphs that represent the time when the iOLab device was slowing down. Use the Select region tool to highlight the part of the graph that represents the device slowing down. Q1.1: Insert a graph of the accelerometer data showing when the iOLab device was pushed and slowing down. Be sure it is zoomed in. Use the Select region tool to highlight the portion where the device is slowing down. Only the y-axis should be displayed.
- Record the average acceleration (μ) and standard deviation (σ) during this time from the Accelerometer graph and the Acceleration vs time graph. (You can see that the acceleration is negative so we could call this negative acceleration or deceleration.)
- Record the time interval, Δt, from the Accelerometer graph and the Acceleration vs time graph. Note that the time intervals may be different for each sensor. This is because the accelerometer sensor collects twice as much data as the Wheel Acceleration sensor.
- Calculate the number of measurements, N, each sensor took. To do this, multiply the time interval, Δt, by the frequency at which the measurements are taken. You can find the frequency of each sensor to the right of the graphs. The unit of frequency is Hertz, abbreviated Hz. For example, in the sample data above, the time interval for the accelerometer sensor was 0.4584 s and the frequency was 200 Hz. So the sensor took 91 measurements during this time. So N = 91.
- In order to compare the data you collect in this lab, you will need to write it out in the following way: mean ± standard error of the mean. You already recorded the means, μ, from the acceleration graphs. Standard error of the mean can be calculated by dividing the standard deviation, σ, by the square root of the number of measurements, N. Record your accelerometer data in the form of mean ± standard error of the mean (
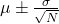 ) Q1.2: Record your accelerometer data in the form of mean ± standard error of the mean. Q1.3: Record your wheel sensor acceleration data in the form of mean ± standard error of the mean.
) Q1.2: Record your accelerometer data in the form of mean ± standard error of the mean. Q1.3: Record your wheel sensor acceleration data in the form of mean ± standard error of the mean. - Q1.4: Compare the accelerometer and wheel sensor data. Which one do you think is more accurate? Why?
Part 2: Collecting Data at Rest and Falling
- Click the Reset button
 . Then place the device on a flat surface wheel side up and begin recording. Q2.1: Record the average acceleration along the z-axis of the Accelerometer sensor while the iOLab device is at rest. Q2.2: What did you think it would read? Why?
. Then place the device on a flat surface wheel side up and begin recording. Q2.1: Record the average acceleration along the z-axis of the Accelerometer sensor while the iOLab device is at rest. Q2.2: What did you think it would read? Why? - Now lift the iOLab device a couple feet in the air. Again, orient it so that the wheels are facing up. Then, with someone prepared to catch it, start recording data and drop the IOLab device. Q2.4: Record the average acceleration from the Accelerometer sensor while the IOLab device was falling. Q2.5: What did you think it would read? Why?
Accelerometer sensors are tricky to understand. They don’t always do what we would expect them to do. When you pushed the device horizontally, the data you collected indicated that the sensor was measuring the rate at which the iOLab device was slowing down. But when you dropped it, it appeared to measure something different. The difference was that gravity was involved in the vertical direction and not in the horizontal direction. Whenever you are using an accelerometer sensor to determine actual changes in velocity, you have to consider whether or not gravity is affecting the measurement. If any part of your measurement involves the z-axis, or some portion of it, gravity has to be factored in. The calculation to factor gravity out is very complicated but if you want to measure acceleration with gravity factored out there are phone apps that do this.
Part 3: Noise
When you zoomed in on your graphs, you should have noticed that the line was not completely flat. Even in Part 2 where you just had the iOLab device sitting flat on the table and not moving, the line was not flat. If you didn’t notice that before, go zoom in now to see.
What you are seeing is called “Noise” or “Random Uncertainty”. This type of uncertainty is caused by unknown or unpredictable changes. They usually have a normal distribution. Export the data from the accelerometer when the IOLab device was at rest. To do this, click on the Save button ![]() and choose “Unique CSV file” and save the csv file to your computer. You will need the data from the Az column. Make a copy of this spreadsheet: Normal Distribution Spreadsheet. Paste your accelerometer sensor data into Column B of this spreadsheet. You should get a nice bell curve shape. Q3: Insert a screenshot of your Normal Distribution.
and choose “Unique CSV file” and save the csv file to your computer. You will need the data from the Az column. Make a copy of this spreadsheet: Normal Distribution Spreadsheet. Paste your accelerometer sensor data into Column B of this spreadsheet. You should get a nice bell curve shape. Q3: Insert a screenshot of your Normal Distribution.
Grading Rubric:
Points are assigned for each question according to the following:
| 1.1 | 3 Points – ALL of the following are true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is slowing down.
2 Points – Only TWO of the following are true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is slowing down. 1 Point – Only ONE of the following is true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is slowing down. 0 Points – A screenshot is not included OR the screenshot is taken of the computer screen with a phone camera or similar. |
| 1.2 | 2 Points – BOTH of the following are true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. |
| 1.3 | 2 Points – BOTH of the following are true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. |
| 1.4 | 3 Points – ALL of the following are true: (1) the accelerometer and wheel sensor data are effectively compared, (2) a statement is made regarding which sensor is believed to be more accurate, (3) there is a reasonable explanation of why one sensor is better.
2 Points – Only TWO of the following are true: (1) the accelerometer and wheel sensor data are effectively compared, (2) a statement is made regarding which sensor is believed to be more accurate, (3) there is a reasonable explanation of why one sensor is better. 1 Point – Only ONE of the following is true: (1) the accelerometer and wheel sensor data are effectively compared, (2) a statement is made regarding which sensor is believed to be more accurate, (3) there is a reasonable explanation of why one sensor is better. 0 Points – No attempt was made to compare the data. |
| 2.1 | 2 Points – BOTH of the following are true: (1) the average acceleration is recorded, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the average acceleration is recorded, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the average acceleration is recorded, (2) appropriate units are used. |
| 2.2 | 2 Points – BOTH of the following are true: (1) there is a statement of what the student thought the sensor would read, (2) there is an explanation of why the student thinks this.
1 Point – Only ONE of the following is true: (1) there is a statement of what the student thought the sensor would read, (2) there is an explanation of why the student thinks this. 0 Points – No attempt was made. |
| 2.3 | 3 Points – ALL of the following are true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is falling.
2 Points – Only TWO of the following are true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is falling. 1 Point – Only ONE of the following is true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details, (3) the Select region tool highlights only the portion where the device is falling. 0 Points – A screenshot is not included OR the screenshot is taken of the computer screen with a phone camera or similar. |
| 2.4 | 2 Points – BOTH of the following are true: (1) the average acceleration is recorded, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the average acceleration is recorded, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the average acceleration is recorded, (2) appropriate units are used. |
| 2.5 | 2 Points – BOTH of the following are true: (1) there is a statement of what the student thought the sensor would read, (2) there is an explanation of why the student thinks this.
1 Point – Only ONE of the following is true: (1) there is a statement of what the student thought the sensor would read, (2) there is an explanation of why the student thinks this. 0 Points – No attempt was made. |
| 3 | 3 Points – ALL of the following are true: (1) a bell curve of the normal distribution is present, (2) a scatter type plot is used, (3) the bell curve has two tails at 0 on the y-axis.
2 Points – Only TWO of the following are true: (1) a bell curve of the normal distribution is present, (2) a scatter type plot is used, (3) the bell curve has two tails at 0 on the y-axis. 1 Point – Only ONE of the following is true: (1) a bell curve of the normal distribution is present, (2) a scatter type plot is used, (3) the bell curve has two tails at 0 on the y-axis. 0 Points – No attempt was made to make a normal distribution. |

