4 Evaluating a Claim II
In this lab you will be presented with a scenario and a statement that makes a claim about the scenario. You will design and conduct an experiment to evaluate the validity of the claim.
Lab 4 Worksheet Evaluating a Claim II
Learning Goals:
- Use data to test and evaluate a claim.
- Use a t-test to determine if two measurements can be considered the same or different.
Experiment
Scenario: An IOLab is placed wheel side down at the bottom of a ramp and given a push so that it rolls up the ramp and then rolls back down the ramp.
Claim: “The acceleration of the IOLab device is the same rolling up the ramp as it is rolling down the ramp.”
Before completing the experiment, ask the following questions: Based on your understanding of acceleration, should the claim be true or false? Why?
- Design and carry out an experiment that will determine whether or not this claim is true. Hint: you will want to use a velocity vs time graph to collect and analyze your data. (Basically, we want to know if we can consider the uphill acceleration and downhill acceleration to be the same.)
- Do a running average to determine when you have enough data. For this experiment, you can determine what a reasonable change in average is. You can do a running average or either the uphill acceleration or the downhill acceleration. It is not necessary to do both.
- Identify the parts of the graph that represent the iOLab device moving up the ramp and moving down the ramp.
- Record the uphill and downhill accelerations in the format of mean ± standard error of the mean. (Recall from Lab 2 that standard error of the mean is
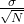(standard deviation divided by the square root of the number of data points.) - Represent these two accelerations graphically with error bars to show similar or different they are. See video below.
- Perform a t-test to determine whether or not the claim is true. See video below.
T Test & Error Bars
A T Test is a way to compare two values and determine whether they can be considered the same or not. You can make a copy of this spreadsheet to calculate it: T Test Spreadsheet. See the video below for details on how to use the spreadsheet to perform the t test.
Grading Rubric:
Points are assigned for each worksheet question according to the following:
Lab 4 Grading Rubric 131 Manual
| 1 | 2 Points – The claim is stated to be either true or false.
0 Points – The claim is NOT stated to be either true or false. |
| 2 | 2 Points – Reasonable reasons are given.
0 Points – No attempt was made or no reasons were given. |
| 3 | 4 Points – BOTH of the following are true: (1) there is a screenshot of the running average from the spreadsheet, (2) a reasonable change in average was identified and reached.
2 Points – Only ONE of the following is true: (1) there is a screenshot of the running average from the spreadsheet, (2) a reasonable change in average was identified and reached. 0 Points – NEITHER of the following is true: (1) there is a screenshot of the running average from the spreadsheet, (2) a reasonable change in average was identified and reached. |
| 4 | 2 Points – BOTH of the following are true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details.
1 Points – Only ONE of the following is true: (1) a professional looking screenshot is included, (2) the graph is zoomed in to show all the details. 0 Points – A screenshot is not included OR the screenshot is taken of the computer screen with a phone camera or similar. |
| 5 | 2 Points – BOTH of the following are true: (1) the portion of the graph when the device is moving uphill is clearly identified, (2) the portion of the graph when the device is moving downhill is clearly identified.
1 Point – Only ONE of the following is true: (1) the portion of the graph when the device is moving uphill is clearly identified, (2) the portion of the graph when the device is moving downhill is clearly identified. 0 Points – NEITHER of the following is true: (1) the portion of the graph when the device is moving uphill is clearly identified, (2) the portion of the graph when the device is moving downhill is clearly identified. |
| 6 | 2 Points – BOTH of the following are true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. |
| 7 | 2 Points – BOTH of the following are true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used.
1 Point – Only ONE of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. 0 Points – NEITHER of the following is true: (1) the data is in the form of mean ± standard error of the mean, (2) appropriate units are used. |
| 8 | 2 Points – BOTH of the following are true: (1) the two accelerations are represented with a dot, (2) the accelerations have error bars that can be compared with an appropriate y-axis.
1 Point – Only ONE of the following is true: (1) the two accelerations are represented with a dot, (2) the accelerations have error bars that can be compared with an appropriate y-axis. 0 Points – NEITHER of the following is true: (1) the two accelerations are represented with a dot, (2) the accelerations have error bars that can be compared with an appropriate y-axis. |
| 9 | 2 Points – There is an accurate description of how the t test was performed.
0 Points – There is an inaccurate description of how the t test was performed. |
| 10 | 4 Points – BOTH of the following are true: (1) the claim is stated as either true or false, (2) there is an accurate explanation for the result.
2 Points – Only ONE of the following is true: (1) the claim is stated as either true or false, (2) there is an accurate explanation for the result. 0 Points – NEITHER of the following is true: (1) the claim is stated as either true or false, (2) there is an accurate explanation for the result. |
