Discussion 2

Instructions: Upload your work as a pdf document. All responses must be typed. Any calculations must be done using Latex, an equation editor, or typed. You can insert diagrams and pictures where appropriate but pictures of your hand written responses and calculations will not be accepted.

Vectors

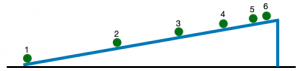
1. Figure 1 shows the motion diagram for a ball rolling up an inclined plane. Each point represents the location of the ball at 1 second intervals. At point 6 the ball turns around and rolls back down the plane (that diagram is not shown). Draw vectors to represent the instantaneous velocities at points 1 and 2. Be sure to draw them pointing in the proper direction.
2. What would the vectors representing the instantaneous velocities and points 3 and 4 look like? How would these vectors compare to the vectors representing points 1 and 2? How would they differ?
3. Draw a vector to represent the acceleration between points 1 and 2. Is the direction of this vector the same or opposite of the velocity vector? Why?
4. As the ball rolls up the inclined plane, what happens to its acceleration?
5. How would the acceleration vector between points 3 and 4 compare to the acceleration vector between points 1 and 2? How would the acceleration vector between points 1 and 4 compare to the acceleration vector between points 1 and 2 or points 3 and 4?
6. What can you conclude about the direction of velocity and the direction of acceleration for a ball rolling up an inclined plane?

Two Dimensional Motion

The following simulation may help with the rest of this assignment. Try the “Circular” and “Ellipse” motions and observe how the velocity and acceleration vectors behave. You can also use the “Remote Control” feature to control the ladybug’s motion manually.

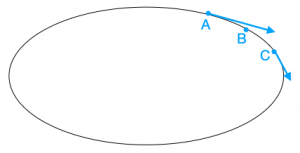
7. In Figure 2, a car drives around an oval racetrack in the clockwise direction. Points A and C show the velocity vectors while the car’s speed is decreasing. Draw the velocity vector for point B.
8. Draw a vector to represent the acceleration at point A. Describe what happens to the angle between the velocity vector and acceleration vector at point A when the car is moving with a constant speed, increasing speed, and decreasing speed.

9. Table 1 shows the velocity and acceleration vectors for a car driving at four different instants in time. Determine if the car is speeding up, slowing down, or moving with a constant speed.
10. For each of the instants in time, draw the velocity and acceleration vectors tail to tail and draw the parallel and perpendicular components of the acceleration vector. Figure 3 shows you what this should look like for time 2.

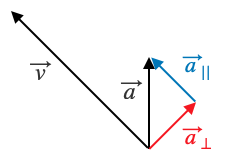
11. Compare your answers from question 9 and your diagrams in question 10. What is always true about the car’s motion when there is a component of the acceleration vector that is parallel to the velocity vector? What is always true about the car’s motion when there is a component of the acceleration vector that is antiparallel to the velocity vector? What is always true about the car’s motion when there is only a perpendicular component of the acceleration vector?